Matlab软件在牛顿环实验数据处理方法上的创新

徐少刚，夏雪琴

(浙江海洋学院，浙江舟山 316022)

牛顿环实验是一个古老而又非常重要的光学实验，一般用它来测量平凸透镜的曲率半径十分方便，这个实验在我校已开设许多年了。目前数据处理方法主要有:逐差法和最小二乘法，用人工计算既繁琐又篇幅大，占用了我们学生较多的学习时间，并且往往运算容易出差错，得不到十分理想的实验结果，这样必然会影响学生的学习积极性和教学效果。随着计算机软件的迅速发展，如用Matlab软件的功能函数进行最小二乘法曲线拟合，得到平凸透镜的曲率半径，而且还能进行误差理论分析，一方面简化了数据处理过程，提高了实验结果的准确度;另一方面提高了大学生应用软件的能力，并且对实验数据处理方法上的一种创新，激发了大学生对学习大学物理实验的兴趣，提高了教学质量。

1 实验原理

在一块平面玻璃上安放上一焦距很大的平凸透镜，使其凸面与平面相接触，在接触点附近就形成一层空气膜。当用一平行的准单色光垂直照射时，在空气膜上表面反射的光束和下表面反射的光束在膜上表面相遇相干，形成以接触点为圆心的明暗相间的环状干涉图样，称为牛顿环，其如图1。

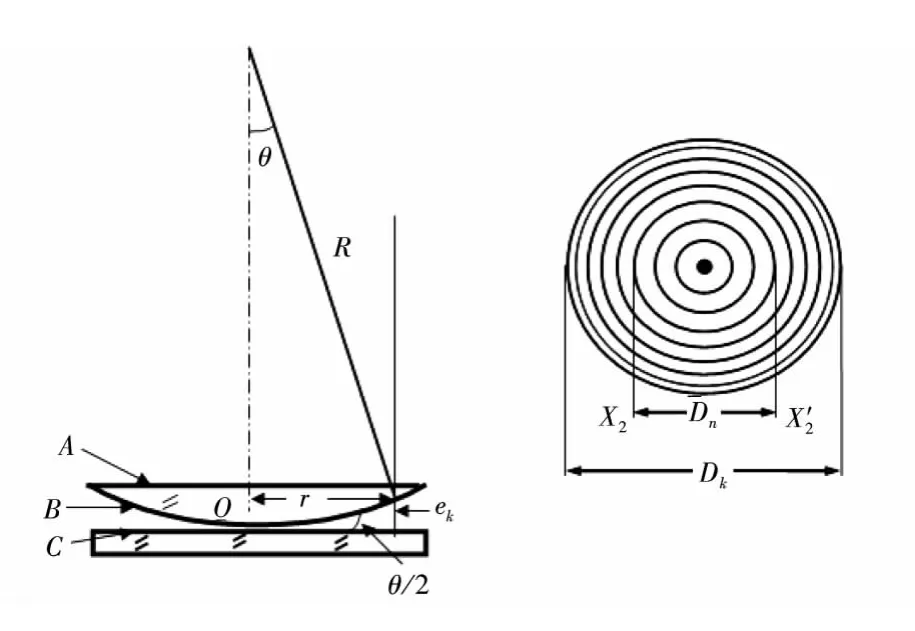
图1 牛顿环光路示意图

可改为 D2K=4KRλ(K=0，1，2，…)

用Matlab软件作图并处理实验数据，作出D2K～K的关系图。

令y=D2K;x=K;k=4Rλ，可得到拟合直线方程y=kx+b，并从其斜率k中求出平凸透镜曲率半径R的值。

2 实验数据记录

已知钠光的波长 λ =5.893×10－7m，仪器误差5 × 10－6m，R标=0.880 0 m，见表1。

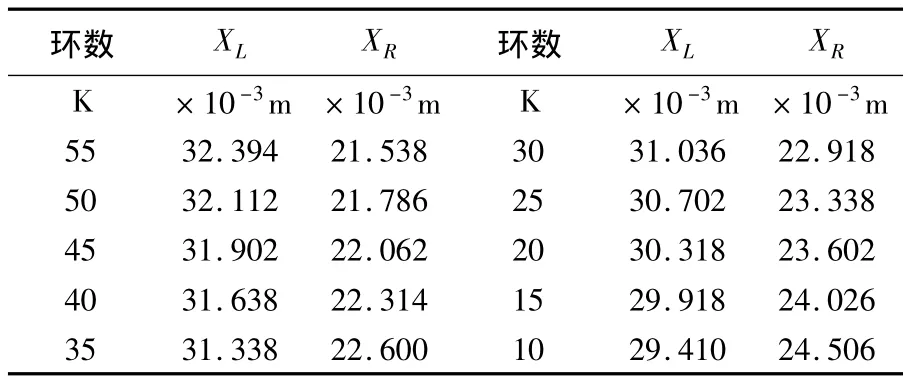
表1 透镜曲率半径测量数据

3 Matlab软件处理实验数据

3.1 得到y与x的数据表

令DK=XL－XR，x=K，y=DK2，用Matlab软件编写程序计算:

＞ ＞ x= ［55 50 45 40 35 30 25 20 15 10］

＞ ＞ c1= ［0.032394 0.032112 0.031902 0.031638 0.031338 0.031036 0.030702 0.030318 0.029918 0.02941］

%XL的值

＞ ＞ c2= ［0.021538 0.021786 0.022062 0.022314 0.0226 0.022918 0.023338 0.023602 0.024026 0.024506］

%XR的值

＞＞c3=c1－c2

%DK=(XL－XR)的值

＞ ＞ y=c3.^2%

y-DK2的值

数据见表 2［2］。

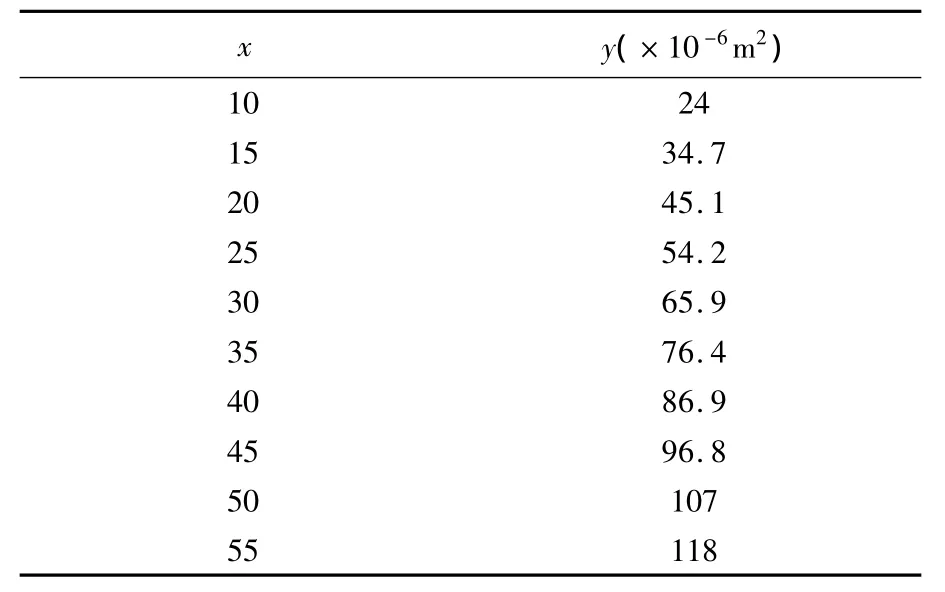
表2 由D2K与K之间关系得到y与x的数据

3.2 用polyfit功能函数作y与x的拟合图

3.2.1 用Matlab软件最小二乘法公式求出斜率k、相关系数γ

y=kx+b用最小二乘法求出曲线的斜率k、相关系数γ，

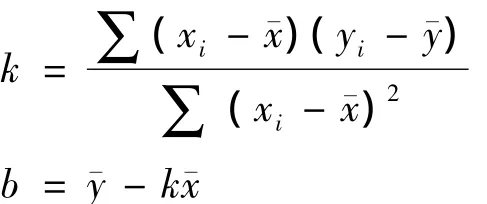
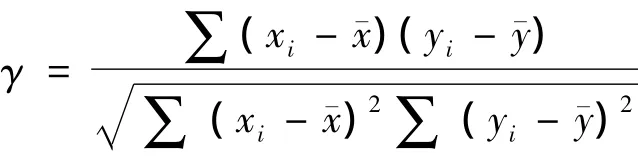
Matlab程序:

＞ ＞ a=polyfit(x，y，1)

结果得:k=0.2079e－ 5，b=0.3307e－ 5

3.2.2 用plot函数绘y与x的拟合图2

Matlab程序:

＞ ＞x1=10:5:55;k=2，

＞＞y1=a(1)*x1+a(2);

＞ ＞ plot(x，y，’* ’，x1，y1，’k’)，xlabel(‘P’)，ylabel(‘I’)，grid on，

Matlab拟合图，见图2。

图2 Matlab绘y与x的拟合图

所以拟合直线方程为:y=0.207 9×10－5x+0.330 7 × 10－5

4 Matlb软件最小二乘法误差分析计算

4.1 Matlab 程序

＞ ＞ yn=a(1)*x+a(2)，xn=(y－a(2))/a(1)，

＞ ＞ sigmayn=sqrt((yn－y)*(yn－y)’/(k*(k－1)))，

%DK的绝对误差ΔY

＞ ＞ sigmaxn=sqrt((xn－x)*(xn－x)’/(k*(k－1)))，

%K的绝对误差ΔX

＞ ＞ xp=mean(x)，yp=mean(y)，

Lxx=(x－xp)*(x－xp)’，

%

＞ ＞ Lxy=(x－xp)*(y－yp)’，

Lyy=(y－yp)*(y－yp)’，

＞ ＞ r=Lxy/sqrt(Lxx*Lyy)，

线性相关系数r

＞ ＞ R=a(1)/(4*5.893*0.0000001)，

%曲率半径¯R

＞ ＞ R0=0.88，deth=(R － R0)/R0，

%百分差ER

＞ ＞ y2=0.000107，x2=50，b=a(2)，

＞＞sigmah=R*sqrt((sigmayn/(y2－b))^2+(sigmaxn/x2)^2)，

%ΔR

＞＞deth1=sigmah/R，

%相对不确定度E¯R

4.2 误差结果得

sigmayn=9.9912e － 007

sigmaxn=0.4807

sigmah=0.012

r=0.9999

R=0.8818

deth=0.0020

death1=0.0136

线性相关系数r=0.9999接近于1，说明k、b的值准确性高且可用，拟合直线方程为:y=0.2079 ×10－5x+0.3307 ×10－5线性拟合度高。

曲率半径的最佳值:¯R0.881 8 m，

D2K的绝对误差 ΔY=sigmayn=9.991 2e－007，

K 的绝对误差 ΔX=sigmaxn=0.480 7，R 的绝对误差 ΔR=sigmah=0.012。

5 实验结论

通过上面用Matlab软件的功能函数对实验数据进行处理，很快得到如下实验结果:

平凸透镜的曲率半径:

R=¯R±ΔR=(8.82±0.12)×10－1m

相对不确定度:

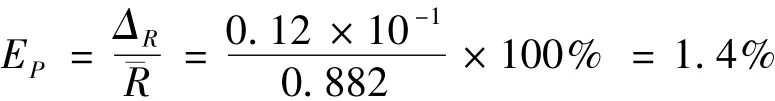
百分差:

根据上面的数据处理和误差分析可知，Matlab软件的功能函数最小二乘法对牛顿环实验进行数据处理精度高，而且程序运行简便，计算快捷、高效;因此，大学生在物理实验中用Matlab软件对牛顿环实验进行数据处理，是对传统的数据处理方法上的一种创新，提高了大学生学习积极性，同时也提高了大学物理实验的教学质量。

［1］王晓雄.利用Origin拟合方法处理牛顿环数据［J］.大学物理实验，2011，24(2).

［2］刘浩.新型基于彩色荧光灯的牛顿环实验［J］.大学物理实验，2012，25(5).