阻尼振动的Mathematica模拟

谢文海，吉 莉，滕艳萍，杨 硕*

(1.大连大学，辽宁 大连 116622;2.大连科技学院，辽宁大连 116035)

阻尼振动是自然界普遍存在的一种振动形式，是振动系统本身的性质与外界共同作用的结果。阻尼振动［1］是物理学和工程领域的一种常见的物理现象，工程中常见的阻力有各种不同的形式，如物体在液体和气体中振动时的粘尼力;物体沿接触面振动时的滑动和滚动摩擦力;材料本身的内摩擦如电磁学实验中导线的内阻等等，其特性在实际问题中较为常见，应用较广。

Mathematica［2］是美国 Wolfram Research 公司开发的数学软件，Mathematica具有运算准确，方便简洁，易于操作和直观等优点。利用它可以进行微分、积分、向量、矩阵的运算以及方程式求解、运算式的化简和展开、因式分解、数值分析等数学运算，同时它还具有强大的绘图功能和交互操作功能，可以绘制出精美的二维图，三维图等。Mathematica强大的功能，使其广泛运用数学、物理、生物、金融等领域的科研和教学中。已有研究表明Mathematica辅助理论力学将有助于优化教学效果［3］。利用Mathematica中傅里叶变换可帮助分析阻尼运动信号的频谱和能谱［4］。

以弹簧振子为例，利用Mathematica简化阻尼振动的理论计算，推导阻尼振动的基本原理，展现基本规律，利用Mathematica傅里叶变换对阻尼运动进行分析，并用图像清晰直观展现阻尼振动的规律。研究运用Mathematica计算和模拟阻尼振动，形象直观的展现阻尼振动的特点，以期为相关的教学研究和工程分析提供有益借鉴。

1 阻尼振动的Mathematica符号计算和数值模拟

运用Mathematica来计算阻尼振动。以水平弹簧振子为例，在阻尼运动中，物体在水平方向受到轻质弹簧的弹性力以及阻力的作用。振动速度较小时，阻尼力F的大小与振动质点的速度的大小成正比，方向相反，表示为F=－kx。这里以弹簧振子为例，振动系统方程可写为

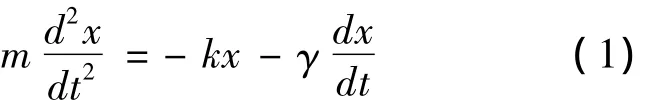
式中:γ为阻力系数，k为弹簧系数;将两边都除以m，同时令为振动系统固有圆频率，β为阻尼系数，即上式表示为

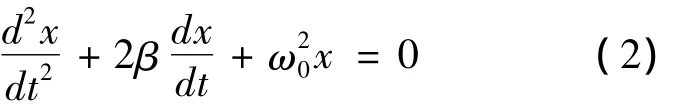
在Mathematica面板中利用DSolve来解二阶常微分方程，如下

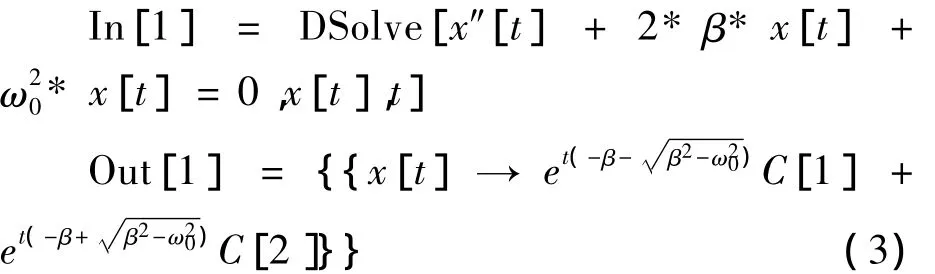
根据ω0，β的关系可以将阻尼分为三种类型，当β＜ω0时，振动系统是欠阻尼振动，我们利用数值模拟来探究阻尼振动的规律。取β=，ω0=15，假设初值条件x'［0］=0，x［0］=3，输入函数表达式，振用Mathematica可作出x-t图，如图1所示。在Mathematica窗口输入下列式子:

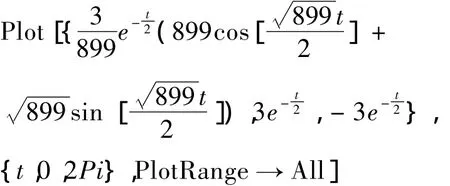
图1 当ω0＜β时，阻尼振动振动的图像

我们还可以探究在相同初始条件下，ω0和β不同时研究阻尼振动的图像［5］。

选取 ω0=2β，ω0=5β，ω0=10β 的振动图像，并对比如图2所示。

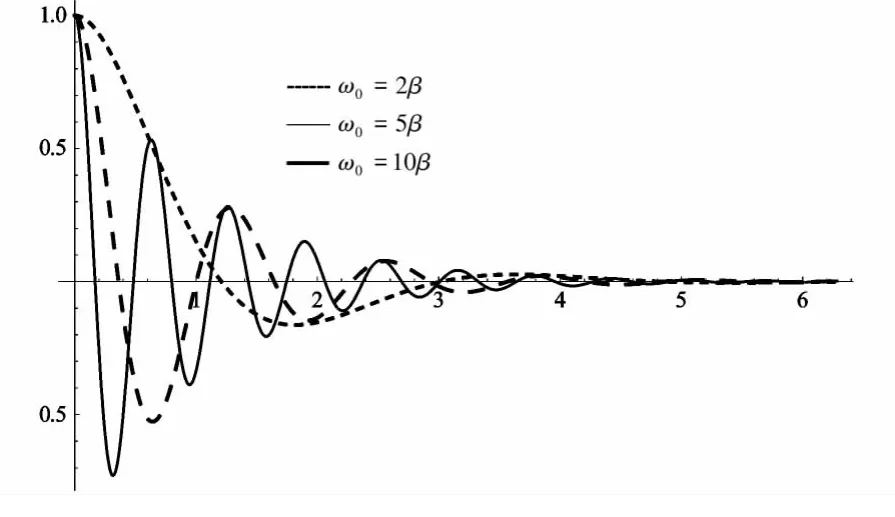
图2 相同初始条件下 ω0=2β，ω0=5β，ω0=10β的振动图像对比

由图像分析，ω0和β相差较小时，振幅减小较大，振荡时间越短;ω0和β相差较小时，振幅减小较大，振荡时间越短。

当β=ω0时振动系统为临界阻尼。这里将阻尼系数和振动圆频率改成β=ω0=3同理操作可得x-t图见图3。由图可知，当β=ω0时，质点从振动处迅速移向平衡位置停止振动，即为临界阻尼振动。

图3 当β=ω0=3时，临界阻尼振动的图像

当β＞ω0时，振动系统为过阻尼振动，取ω0=2，β=5，同理操作作出x-t图如图3所示。由图可知，当β＞ω0时，质点将从振幅处向平衡位置缓缓移动，且停止振动前经历时间较长，则为过阻尼振动，见图4。

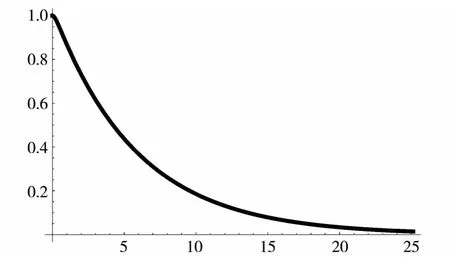
图4 当β＞ω0时，过阻尼振动的图像

根据图像可以得到β与ω0的比值(也就是阻尼比的大小)不同有不同的振动规律，我们通过Mathematica展现出来的非周期性阻尼振动形象生动，易于理解。通过图像可以知道不同的阻尼比所表示的阻尼振动有不一样的振动特点，因而为了更精确地表达，我们需要掌握好阻尼比阻尼因子，可以利用Mathematica将阻尼振动，临界阻尼振动和过阻尼振动图像结合在一起，清楚直观的对比阻尼振动的规律。此外还可以探究不同初始条件下，阻尼运动，欠阻尼运动和过阻尼运动规律的不同，见图5。

图5 阻尼振动，临界阻尼振动，过阻尼对比图线

2 对阻尼振动的Mathematica傅里叶分析

如上分析，阻尼振动的规律比较复杂，不可能是单一频率的振动，由傅里叶分析可知阻尼振动是无穷多个正弦振动和余弦振动所组成，其频率是从0～∞。系统的能谱不是系统的真是能量，如动能，势能，机械能等，而是表示频率分量振幅的平方，是一个衡量不同成分贡献的一个方便表示。因此分析能谱能找出频率分量的特征。利用Mathematica软件中傅里叶分析探究分析弹簧的能谱。

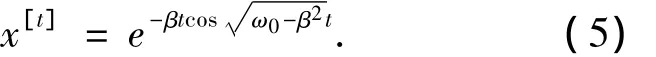
利用Mathematica对此式进行傅里叶变换［6-7］，并已知 t≥0，ω，ω0，β 为实数。如下

引入傅里叶强度 I(ω)=A2+B2，并用Simplify进一步简化可得，

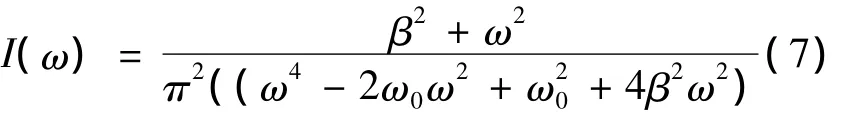
可以利用mathematica软件中Manipulate命令实现人机交互，它包含一个或多个控件滑块，移动滑块能动态改变多个参数的数值，图像可实现即时更新动态演示［4］。改变 ω0，β 大小，分析阻尼振动强度的变化。如下

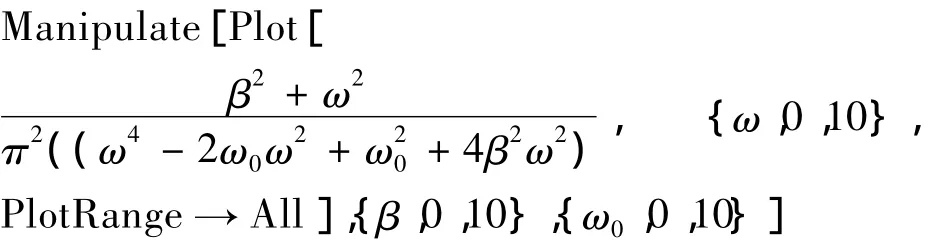
由于讨论弱阻尼运动，即β2＜＜ω0，其傅里叶强度如图6所示，当β2＜＜ω0时，β不变时，弹簧能谱最大值随着ω0的增大而增大，ω0不变时，弹簧能谱宽度随着β的增大而增大。β较小时，系统的谱线较窄，单色性较好。

图6 β2＜＜ω0β，ω0不同时傅里叶强度的变化

3 结 论

通过Mathematica我们可以将不同条件下的阻尼振动形象地展现出来，体现了mathematica软件对曲线非线性拟合的强大功能，以及对数据的精确处理，更加清晰直观的解释了阻尼振动的原理和规律，这对物理学中研究阻尼振动提供了更方便更有利的工具。

［1］漆安慎，杜禅英.力学［M］.2版，北京:高等教育出版社.

［2］［M］.赫孝良，周义仓，译.西安:西安交通大学出版社，2002.

［3］杨硕，谢文海，霍飒.Mathematica在理论力学教学中的应用［J］.湖北师范学院学报:自然科学版，2014，31(1):82-86.

［4］董键.Mathematica与大学物理计算［M］.北京:清华大学出版社，2013.

［5］彭楚西，姚进斌，田超等.浅析Mathematica阻尼振动在实验当中的应用［J］.科技信息，2010，32，525.

［6］刘果红，盛守奇.阻尼振动的傅里叶分析［J］.安徽建筑工业学院学报:自然科学版，2005，13(2):7-8.

［7］王明美.“几何画板”绘制机械振动的关系图示［J］.大学物理实验，2013(4):13-15.