基于风险分析的军用危险品道路运输线路优化

我国的军用危险物资一般有武器弹药(包括报废弹药)、火箭推进剂、各种油料等3 大类［1］。在运输的过程中，若发生爆炸，可引燃周围可燃物而酿成火灾，爆炸气体形成的空气冲击波，可造成对周围的破坏，严重的可摧毁附近的建筑物及设施并造成人员伤亡。

军用危险品从生产到储存、使用都需要通过运输环节才能实现其战斗力，道路运输网的建设给军用危险品运输提供了快捷通道，但由于其具有特殊的理化性质，无论是平时还是战时，都具有极大安全隐患［2］。若发生运输事故，不仅会污染环境，而且会因未能及时补充作战物资而影响部队战斗力。运输线路优化不仅要节约成本，最重要是降低风险。因此，针对降低运输风险的军用危险品道路路线优化研究具有一定的现实意义。

1 危险品运输风险分析

军用危险品道路运输是由人员、运输工具、公路线路、装载货物及周围不断变化的环境等组成的系统，这个系统由于受到各种因素的影响而存在安全风险。为降低危险品道路运输的风险，有必要进行风险分析。风险分析是指通过辨识军用危险品运输过程中的影响因素，估计各种因素可能发生的概论，计算出在不同运输条件下的运输风险，从而作出正确判断，其目的在于辨识出影响系统安全的最基本因素［3］。通过分析军用危险品道路运输系统，其风险影响因素主要有相关人员、军用危险品、装卸设施设备、外部环境等。对军用危险品运输的风险分析过程可以看作是公路运输网、运输风险源、影响区域三者交互分析的结果［4］，风险分析的框架如图1 所示。

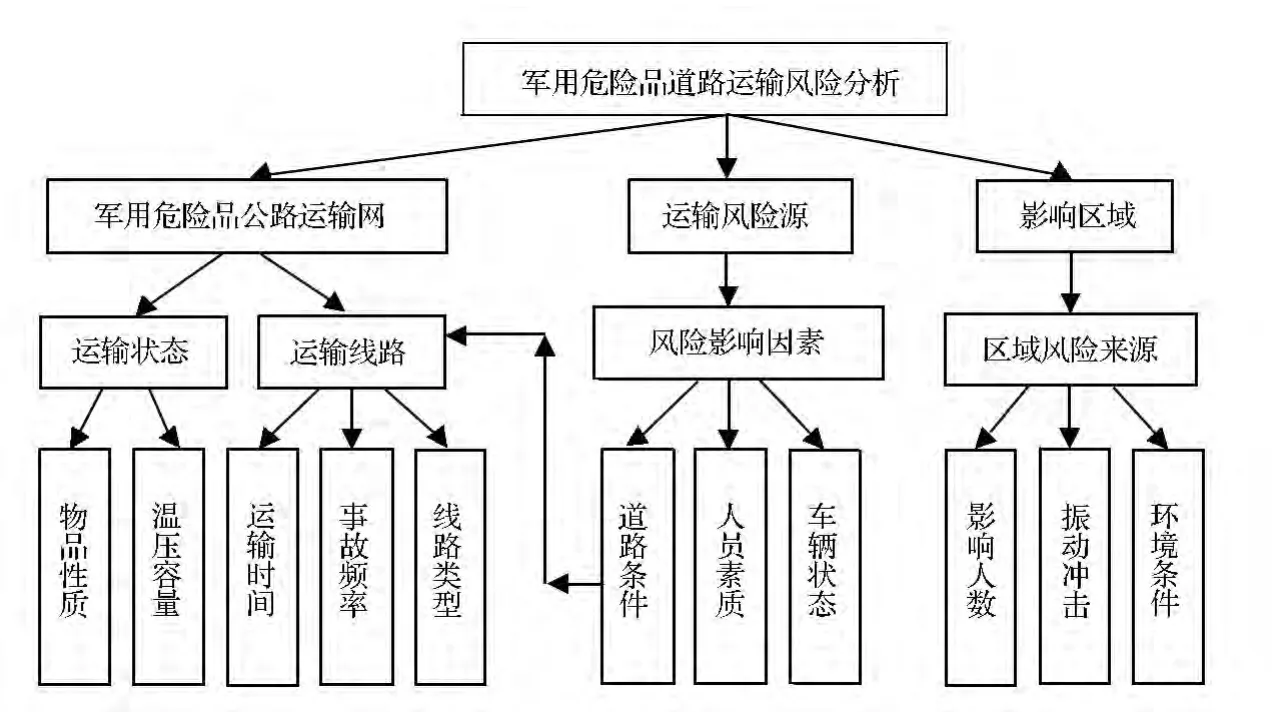
图1 危险品道路运输风险分析框架

危险品公路运输存在的危险点表现在运输网、运输风险源、影响区域3 个方面，而通过图1可以发现，这三者存在着一定程度上的交叉影响，对风险的影响程度不同，危险品运输过程中不同的路线有不同的运输风险。本文选取运输事故率、影响人员数、环境风险、运输时间4 个风险指标，将风险指标作为选线指标，按照权重结合为一个风险值。

2 选线优化

2.1 选线风险影响因素

由于危险品公路运输要考虑的主要问题是减低风险，直接影响到线路优化的方向。线路优化问题即运输路线选择问题，这是个多目标问题;而危险品运输的目的是使得运输风险最小，这就是线路优化的根本目的，线路优化的约束条件则是运输风险的各种影响因素，线路优化要达到这个目的，就要将影响风险的各种因素考虑进去。为了解决这个多目标问题，将风险影响因素转化为风险值来选择最佳路径，同时，依照道路状况，如道路等级、设计限速、交通量等，以及影响人员、天气状况等因素影响运输过程优化选线，而且选线决策中应更多地考虑输沿线影响人员风险［4］。为此，从减小风险的角度使用运输事故率、影响人员数、环境风险、运输时间4 个选线优化指标，并且以最小化运输事故率和最小化影响人员数为主要优化目标来定义风险值。

军用危险品公路运输的可行路径由一系列路段P构成，定义P={1，2，…，n};Pi为第i路段的泄露事故率，事故/a;di为第i路段的路线长度，km;Ci为第i路段风险区的影响人员总数，人;而对于危险品道路运输沿线的影响人员可以分为路上影响人员C1、路外影响人员C2、沿线聚集中心人员C3等3 类［5］。由此可以得到如下的选线评价指标，即选线函数。

(1)运输事故率P:

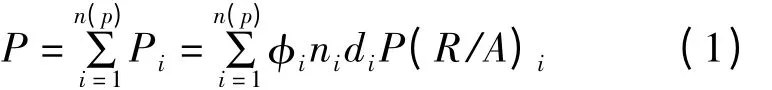
式中:P为总的运输事故率;φi为第i路段危险品的运输事故率;P(R/A)i为第i路段危险品运输事故中的条件泄露概率;ni为第i路段运输车辆数。

(2)影响人员数量C:

(3)环境风险Ε:

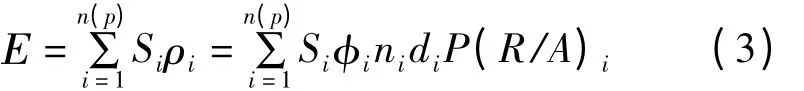
式中:ρi为人员出现的概率;Si为第i运输路段危险品泄露后的影响敏感区环境面积［5］。

(4)运输时间T:

式中Vi为第i路段平均运输速度。

2.2 选线风险值

设选线评价指标m(1≤m≤4)，表示为一个集合fi={f1，f2，…，fm};l为运输起点O至终点D间的一条可行路径，则路径的选线函数可表示为fk，它由多个目标函数组成，由于评价指标都是越小越优，则可表示选线函数为

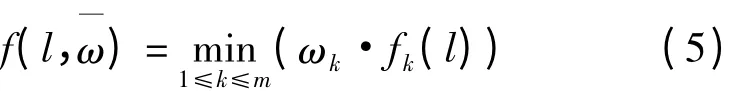
由于各个选线目标函数的单位不同，为了比较，先求解各个目标属性的最小评价值，然后标准化选线函数的单位，使其为无量纲的数值［6］。可将最优线路的评价函数转化为

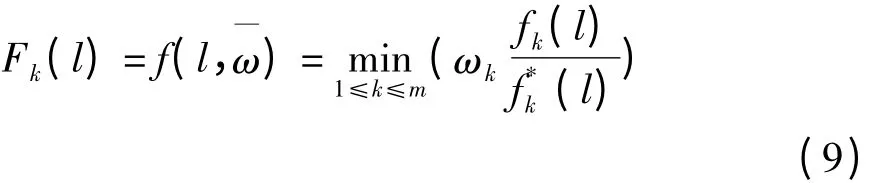
式中:fk(l)为路径第k个选线函数的评价值;f*

k(l)为路径第k个选线函数的最小评价值。则危险品道路运输的风险值可以表示为

2.3 选线方法

路段的风险值由各个目标的风险值组成，需结合Dijsktra 最短路算法求解危险品运输最优路径［7］。该算法求非负赋权图中起点vs到终点vt的最小风险值路线，具体步骤如下。

(1)对于一个有权重的有向图G，以V表示所有顶点的集合，每一个图中的边都是2 个顶点所形成的有序元素对，(u，v)表示从顶点u到v有路径相连，每条边(u，v)赋以一个实数F(u，v)，称为边的权，这里权值F(u，v)取为该路段的风险值F。

(2)若有一条从u到v的边，若是最小权值路径，则把u到v的边加在这条路径后面，得新路径权值为d(u)+F(u+v)，判断其是否小于目前已知的d(v)的风险值;若是，则将d(v)用d(u)+F(u+v)取代，如此扩展计算，可得从起点到终点的最小风险值路线及风险值。

(3)算法中保留顶点集合S与Q，已算出的最小风险值d(v)的顶点放在S中，其他顶点放在Q中，开始时S为空，每一步都会有Q中满足d(u)值最小的点移动到S中来。

(4)最后的结果得到从起点vs到终点vt的一条最小风险路，这条路即是最优路线，该路线总的风险值为各路段风险值之和。

3 实例分析

以某道路运输网为例，该道路拓扑图如图2 所示。设从v0-v7运送10 t 的军用危险品物资，通过调查路段的事故率、影响人员数、环境风险、运输时间等基本信息，建立拓扑如图2 所示。

在给出的危险品道路运输路网拓扑图中，一共有8 个顶点、12 条有向路段，各个路段的相关选线函数的取值见表1。

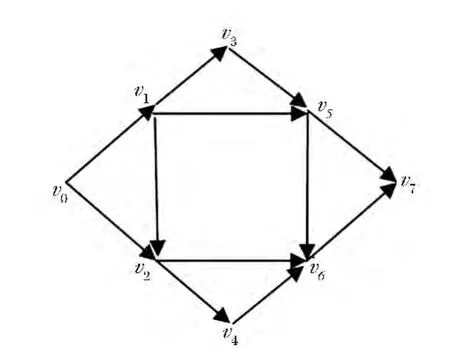
图2 军用危险品道路运输路网拓扑

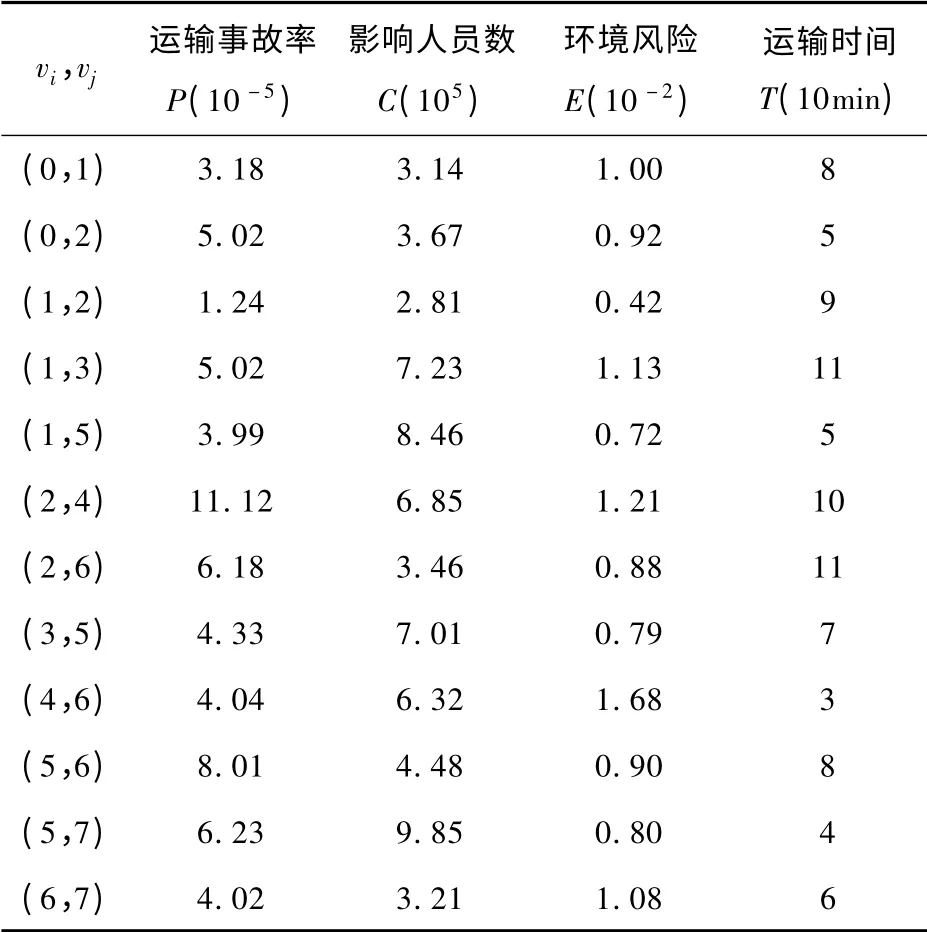
表1 路段取值数据

将各选线值进行标准化处理后，按照其对运输风险值的重要程度，在这里主要依据文献［5］中的权值参考，赋予这几个指标以权重:35% P+30% C+20% E+15%T，结合Dijkstra 最短路算法求解，得到最小风险值路径(用虚线表示)，如图3 所示。

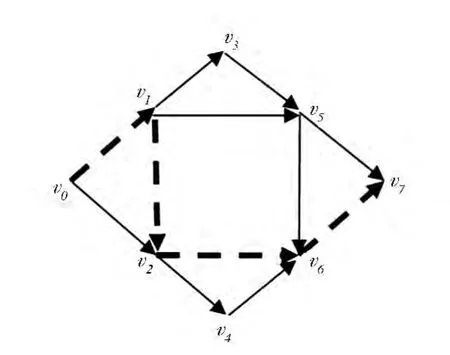
图3 最小风险路线

按照传统的运输方式，为最快速度地运送军用危险品物质，一般会选择运输时间最短的路线lminT为v0-v1-v5-v7，按照本文的综合风险值最小的最短路算法，综合风险最小的路径lminF为v0-v1-v2-v6-v7。对比二者的标准化风险值，lminF(值为2.92)明显地小于lminT(值为3.85)，运输风险值减小24.2%。可见，最短运输距离路线并非最佳路线，传统的最短运输时间方法，虽然节约了运输时间，但会承担很大的运输风险。通过最小风险权值选线方法进行路线优化，虽然增加了运输时间，但极大地减小了运输事故率、影响人员数等，也就减小了运输风险，达到了运输路线优化的效果。

4 结 语

针对降低军用危险品的道路运输中风险的路线优化问题，可以有效地减小运输事故率、影响人员数等，从而最大程度地降低运输风险。本文在对运输风险组成因素进行详细分析的基础上，确定了选线指标，采用最短路径结合的方法寻找最佳的运输路线。通过实例计算结果，表明此方法可较好地应用于军用危险品的运输，能获得最小风险值的最优路线，从而有效平衡各个选线指标，为军事运输选线决策部门提供有一定参考价值的决策技术和方法。

［1］ 高殿森，梅全亭，吕楠. 军用危化物资道路运输环境风险与防范对策探析［J］.中国储运，2010(11):107-109.

［2］ 丁许龙，易云耀，刘俊杰.军用危险品运输风险评估［J］. 商品与质量，2011(S9):175-176.

［3］ 高进东，冯长根，吴宗之.风险分析的质量评价研究［J］. 中国安全科学学报，2001，11(2):65-66.

［4］ 吴宗之，任常兴.危险品道路运输选线问题分析［J］.安全与环境学报，2006，6(2):84-88.

［5］ 任常兴，吴宗之，李晋. 基于风险分析的危险品道路运输多目标Pareto 最优选线［J］. 中国安全生产科学技术，2008，4(2):9-12.

［6］ 毛华，赵小娜，毛晓亮. 危险品运输中的最小风险最大流算法［J］.计算机工程，2012，38(9):268-270.

［7］ 高随祥. 图论与网络流理论［M］. 北京:高等教育出版社，2009:13-15.