基于压杆后屈曲的工程材料形变行为及弹性模量测定

姜 松，施小燕，曾昕鑫，徐 斌

(江苏大学食品与生物工程学院，江苏镇江212013)

弹性模量是材料的基本物理参数，描述弹性材料力学行为的性能指标，是表征材料力学特性的重要参数之一［1-2］.国家标准中测量金属材料弹性模量的静态法有拉伸法和压缩法，GB/T 7314—2005《金属材料压缩试验方法》和GB/T 228—2010《静态拉伸法》虽然方法简便，但是压缩、拉伸载荷大，加载速度慢，拉伸法对试样外形规格也有特定的要求，测量设备庞大复杂，并且影响拉伸性能测量误差的因素很多［3-4］.GB/T 9341—2008《塑料弯曲性能测定》中的方法是基于小挠度理论的三点弯曲法［5］，操作不易控制，精度低.压杆后屈曲法是一种操作简便、可靠的测定方法，目前应用于挂面、直米线、钢丝和聚合物等材料的弹性模量测定，但目前后屈曲形变行为参数测定采用接触测量或标尺辅助目测，测量设备庞大复杂或测量精度低、操作复杂［6-12］.本研究基于扫描图像分析法中各种材料压杆后屈曲形变行为参数的测定，验证65Mn钢、20碳钢、不锈钢、铜、PVC、PET、双面高光铜版纸和竹片8种材料的形变行为与压杆后屈曲大挠度理论的吻合性，运用压杆后屈曲法测定材料弹性模量，优化测定条件参数.

1 材料与方法

1.1 试验材料

不同规格的4种金属材料和4种非金属材料，共计8种材料，均为长条型，65Mn钢片、铜片和PET片试样是由塞尺改制而成.基本参数见表1，其中，a，b和l分别为这8种工程材料的宽度、厚度和长度.

表1 试样材料的基本参数 mm

续表

1.2 仪 器

TA-XT2i质地分析仪(英国Stable Micro System公司);HP Deskjet F2488扫描仪(惠普(中国)有限公司);游标卡尺(上海量具刃具厂)，精度为0.02 mm;测厚仪(外径千分尺，上海川陆量具有限公司)，分辨力为0.01 mm;试样夹具是由带微调装置的游标卡尺(上海量具刃具厂)改制，精度为0.02 mm，如图1所示.

图1 后屈曲端部轴向位移量可调的夹具

1.3 试验方法

1.3.1 形变行为参数测定方法

将每根试样分别置于试样夹具的两爪之间(两卡爪预设间距略大于试样理论长度)，通过试样夹具的微调装置使两卡爪之间的距离刚好等于试样的长度;再根据端部转角 5°，10°，15°，20°，25°，30°，35°和 40°对应的端部轴向位移理论值调节微调装置，使试样的端部轴向位移量等于端部轴向位移Δl理论值［10］;然后放置于扫描工作面上，启动扫描仪，对形变试样进行扫描，获取图像，从图像中读取中点挠度和端部转角［13］.扫描仪输出分辨率设置为300 dpi，每组试验平行5次，取均值，并计算误差.试样长度、轴向位移量分别为180，12.14 mm.

1.3.2 弹性模量测定方法

1)压杆后屈曲法.将试样垂直放置在探头和底座平台之间，每次测试一个试样.探头向下移动，使试样发生后屈曲弯曲［7］.物性仪基本设置:探头P100;采用压缩力测量;运行方式:测前速度、测试速度均为0.1 mm·s-1，测后速度 1.0 mm·s-1;仅记录测量行程;启动触发;数据采集速率为100 pps;传感器选5 kg.

探头下压距离设置为端部转角30°轴向压缩位移量 Δl，与长度 180，150，120，100 和 90 mm 对应的Δl近似值分别为 12.2，10.2，8.1，6.8 和 6.1 mm.每种试样平行试验5次，取均值［7］.

2)三点弯曲法.分别对6种不同厚度的65Mn钢片进行3种不同跨度的三点弯曲试验，跨度分别为60，50 和 40 mm，中点挠度为 0.5，1.0，1.5，2.0，2.5 和3.0 mm.

物性仪基本设置:探头HDP-3PB;压缩力测量;运行方式:测前速度、测试速度均为0.1 mm·s-1，测后速度为 1.0 mm·s-1;压缩量:3.5 mm;仅记录测量行程;启动触发;数据采集速率为100 pps;传感器选用5 kg.每种规格试样平行试验3次，取平均值［7］.

2 结果与分析

2.1 形变行为参数的分析

试样在 5°，10°，15°，20°，25°，30°，35°和 40°时，中点挠度实测值与理论值比较结果见表2.8种材料中点挠度实测与理论值误差均在2%以内，尤其是当端部转角大于15°时，除长度为120 mm和100 mm的铜片外，中点挠度的误差均小于1%.端部转角的测定结果与端部转角理论值基本吻合，误差均小于5%，当试样在端部转角20°以后，其端部转角实测值与理论值的误差基本在1%以内.竹片在理论端部转角10°以内，中点挠度和端部转角误差分别小于5%和6%，理论端部转角10°以上中点挠度和端部转角误差分别小于2%.

以上表明这些材料后屈曲形变行为符合压杆后屈曲大挠度理论.但铜片在长度为120 mm和100 mm，厚度为0.40 mm 和 0.50 mm 时，由于厚度过大，当端部转角θ0过大时，铜片会发生明显塑性形变，此时铜片后屈曲形变行为已经不符合后屈曲大挠度理论，因此，当使用压杆后屈曲法测量此规格铜片时，应控制端部转角范围.在竹片后屈曲形变行为特征参数测定中，由于竹片材质特殊性，适当控制试样长度，应尽量保证试样在长度方向上均质性，否则，竹片后屈曲形变出现不完全对称，θ0不等，测量结果与理论值误差较大.

另外，由压杆大挠度理论分析可知，起始阶段后屈曲压杆端部轴向位移量Δl的微小增加，会导致中点挠度明显增大.如当θ0=5°时，端部轴向位移量仅为压杆长度l的2‰，而挠度将达到l的2.8%;当θ0=10°时，Δl仅为l的7.6‰，而挠度将达到压杆长度l的5.5%［12］.因此，在 θ0＜15°测试时，特别是在θ0＜10°测试时，相对其他角度下中点挠度测量误差就比较大.

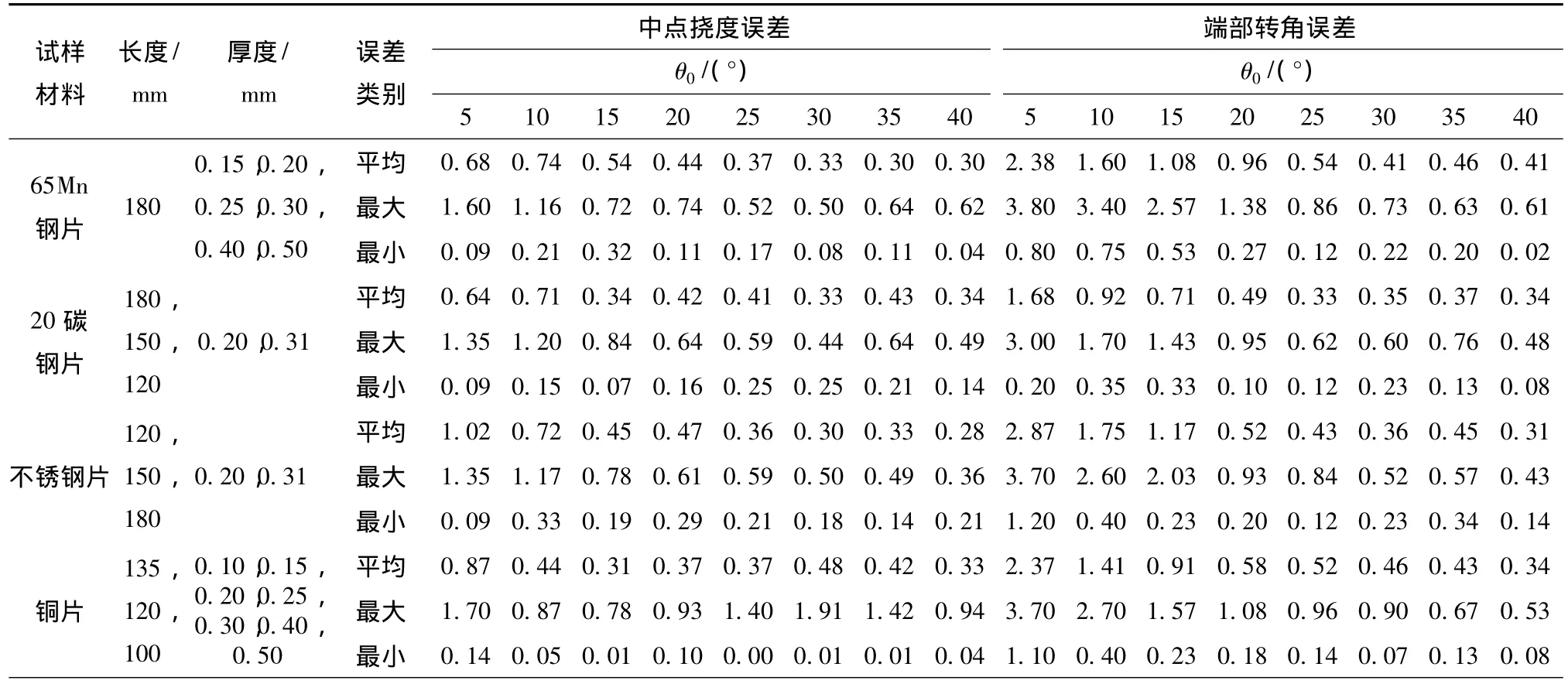
表2 试样压杆后屈曲的中点挠度及端部转角的误差 %

续表

2.2 弹性模量的分析

2.2.1 两种弹性模量测定方法的比较

1)65Mn钢的三点弯曲法弹性模量.表3为65Mn钢片三点弯曲法弹性模量测定值.由表3可知:在同一厚度下，不同跨度对试验结果有影响.当厚度较小且跨度为40 mm时，弹性模量实测值比跨度为50 mm时的大;当厚度较大时，弹性模量实测值随跨度增大而变大.65Mn钢片在厚度为0.25 mm、跨度为60 mm和厚度为0.30 mm、跨度为50 mm时，实测值与公称值较接近，因此测试材料厚度不宜太薄或太厚，测试跨度不能太小.结果表明:三点弯曲弹性模量测定方法受多种因素的影响，测试不易控制.

表3 65Mn钢片三点弯曲法弹性模量测定值 102GPa

2)65Mn钢压杆后屈曲法弹性模量.图2中6条曲线分别为厚度 0.15，0.20，0.25，0.30，0.40 和0.50 mm的65Mn钢片压杆后屈曲法试验曲线，钢片长度均为180 mm.计算得到65Mn钢的弹性模量值(见表4).由于在θ0=5°之前，试样轴向压力处于后屈曲达到稳定的过渡阶段，试样轴向压力变化较大，所以不考虑θ0=5°时的测定值.而6种厚度的试样在θ0为15°时的弹性模量实测值均在公称值内;当θ0=15°～30°时，钢片弹性模量变化不大，测量结果较稳定;厚度0.25～0.50 mm范围内的钢片在各个端部转角测得的弹性模量值更接近公称值，且相对误差小，其中0.40 mm和0.50 mm厚的试样的各端部转角下的测定结果相对误差最小.因此，压杆后屈曲法测定65Mn钢片的最佳厚度为0.25 mm，θ0=15°.

综上所述，压杆后屈曲法优于三点弯曲法.与文献［6］和［7］的结果一致.

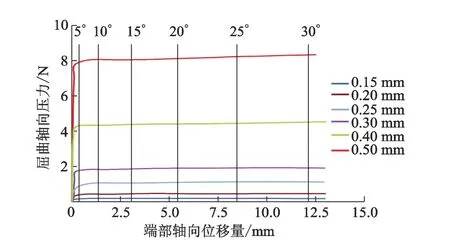
图2 不同厚度65Mn钢片压杆后屈曲法试验曲线

表4 65Mn钢片压杆后屈曲法弹性模量测定值 102GPa

2.2.2 20碳钢、不锈钢及铜片压杆后屈曲法

20碳钢片、不锈钢片和铜片的弹性模量测定结果如表5，6和7所示.试验所用20碳钢和不锈钢弹性模量的公称值为210 GPa，铜片的弹性模量公称值为121 GPa.

在试样长度为180 mm时，碳钢和不锈钢的弹性模量测定值比较集中，即各端部转角下的测定值相对误差小，而长度为120 mm的试样在各个端部转角下的测定值误差最大.各种长度的铜片在θ0=20°下的测定值最集中，其他角度时的测量值都比较分散.

综合考虑试样在各个端部转角下弹性模量测定值的稳定性和准确性，20碳钢片、不锈钢片及铜片这3种金属材料的最佳测试条件分别是:20碳钢片的最佳长度为150 mm，厚度为0.30 mm左右，θ0=20°;不锈钢片的最佳长度是180 mm，厚度为0.20 mm左右，θ0=20°;铜片的最佳长度为120 mm，厚度为 0.30 mm，θ0=20°.

表5 20碳钢片压杆后屈曲法弹性模量测定值 102GPa

表6 不锈钢片压杆后屈曲法弹性模量测定值 102GPa

表7 铜片压杆后屈曲法弹性模量测定值 102GPa

2.2.3 PVC、PET 及铜版纸压杆后屈曲法

PVC、PET及铜版纸弹性模量测定结果如表8，9和10所示.由表8中可知，在 θ0＜20°时，PVC片在5种不同长度的测定结果之间的相对误差较大，而当θ0=25°～30°时，5种长度试样的弹性模量测定值之间相对误差小.同时还可以发现试样长度越长，各角度测定值相对误差越小.其中150 mm长度的试样的弹性模量测定值最稳定.

表8 PVC片压杆后屈曲法弹性模量测定值 GPa

由表9中可知，PET片试样的压杆后屈曲法弹性模量测定中，试样在不同端部转角下的弹性模量测定值波动较大，波动范围最小的是厚度0.50 mm的试样.θ0=20°时，5种厚度的试样的测定结果误差最小，表明在该端部转角下测量 PET片的效果最佳.

表9 PET片压杆后屈曲法弹性模量测定值 GPa

由表10中可知，铜版纸弹性模量的测试中，当试样后屈曲之后，载荷呈现明显地下滑趋势.从表10中还可知，长度为180 mm和150 mm的铜版纸试样弹性模量测定值比其他长度较短的试样大;铜版纸试样的长度为180 mm和90 mm时，各端部转角下的弹性模量测试结果误差较大，而100，120和150 mm长度的试样测定结果误差较小，其中长度120 mm，宽度30 mm的试样测定结果最稳定.

综上所述，压杆后屈曲法测量厚度0.38 mm的PVC片弹性模量的最佳测试长度为150 mm，端部转角为25°.300 g·m-2双面高光铜版纸片弹性模量的最佳测试长度为120 mm，端部转角为25°，宽度为30 mm.长度80 mm的PET弹性模量测定的最佳厚度为 0.50 mm，端部转角为 20°.

2.2.4 竹片压杆后屈曲法

由表11可知，表层(竹青)和中层(竹肉)的弹性模量值相差很大，存在明显的差异，竹表层的弹性模量测定值在14～21 GPa之间，竹中层的弹性模量测定值在8～13 GPa之间.试样的长度对测定结果的影响较大，试样越长，各端部转角时的测定值更接近，且端部转角20°时与25°的测定结果最接近，因此综合考虑上述因素，压杆后屈曲法测量竹片弹性模量的最佳长度为180 mm，端部转角为20°，厚度为1.0 mm 左右.

表11 竹片压杆后屈曲法弹性模量测定值 10 GPa

3 结论

1)利用扫描图像法验证了8种材料，即65Mn钢、20碳钢、不锈钢、铜、PVC、PET、双面高光铜版纸和竹材的后屈曲形变行为符合压杆后屈曲大挠度理论.除竹材外，其余7种材料的中点挠度实测值与理论值的误差都在2%以内;端部转角的测定结果与端部转角理论值基本吻合，误差均小于5%，当试样在端部转角20°以后，其端部转角实测值与理论值误差基本在1%以内.竹材中点挠度误差较大.

2)通过比较三点弯曲法和压杆后屈曲法测量65Mn钢的弹性模量，压杆后屈曲弹性模量测试方法比三点弯曲法更准确、可靠，压杆后屈曲法的测试结果与公称值更吻合.试验表明:基于压杆后屈曲的弹性模量测定方法可以用于65Mn钢、20碳钢、不锈钢、铜片、PVC、PET和双面高光铜版纸以及竹片等工程材料弹性模量的测定.

3)压杆后屈曲法弹性模量测定中，金属材料的最佳测试厚度为0.2～0.3 mm，端部转角为15°～20°，最佳测试长度为 150 ～180 mm;厚度 0.38 mm的PVC片弹性模量测量的最佳长度为150 mm，端部转角为25°;80 mm长度的PET片的最佳测试厚度为0.5 mm 左右，端部转角为 20°;300 g·m-2双面高光铜版纸弹性模量的最佳测试长度为120 mm，端部转角为25°，宽度为30 mm;竹片的最佳测试长度为 180 mm，θ0=20°，厚度为1.0 mm 左右.

References)

［1］Fedorchenko A I，Wang A B，Cheng H H.Thickness dependence of nanofilm elastic modulus［J］.Applied Physics Lettters，2009，94(15):2111-2114.

［2］Lord J D，Morrell R M.Elastic modulus measurementobtaining reliable data from the tensile test［J］.Metrologia，2010，47:S41-S49.

［3］郭天葵.拉伸法测弹性模量实验结果的误差分析［J］.中国现代教育设备，2009，15:82-83.Guo Tiankui.Error analysis of the test results of elasticity modulus tested by the stretch method［J］.China Modern Educational Equipment，2009，15:82-83.(in Chinese)

［4］周明秀，徐 寒，丁中华，等.测量杨氏模量的一种新方法［J］.淮阴工学院学报，2008，17(5):17-20.Zhou Mingxiu，Xu Han，Ding Zhonghua，et al.A new method of measuring Yong's modulus［J］.Journal of Huaiyin Institute of Technology，2008，17(5):17-20.(in Chinese)

［5］Ohtsuki A.An innovative own-weight cantilever method for measuring young's modulus in flexible thin materials based on large deflections［J］.Applied Mechanics and Materials，2010，24/25:371-377.

［6］姜 松，贾 瑜，程红霞，等.基于压杆大挠度理论的挂面弹性模量测定方法［J］.中国粮油学报，2010，25(7):106-109.Jiang Song，Jia Yu，Cheng Hongxia，et al.A determination method of dry noodle elastic modulus based on theory of compressive rod large deflection［J］.Journal of the Chinese Cereals and Oils Association，2010，25(7):106-109.(in Chinese)

［7］姜 松，黄广凤，刘瑞霞，等.压杆后屈曲法测定直条米线弹性模量［J］.农业工程学报，2011，27(1):360-364.Jiang Song，Huang Guangfeng，Liu Ruixia，et al.Compressive rod post-buckling method for straight rice vermicelli elastic modulus determination［J］.Transactions of Chinese Society of Agricultural Engineering，2011，27(1):360-364.(in Chinese)

［8］Ohtsuki A.A new method of measuring young's modulus using postbuckling behavior［C］∥Proceedings of the2006SEM Annual Conference and Exposition on Experimental and Applied Mechanics.2006:1-8.

［9］Ohtsuki A.An innovative method for measuring young's modulus of multi-layered materials using postbuckling behavior［J］.Procedia Engineering，2011(10):1041-1046.

［10］姜 松，刘瑞霞，陈章耀，等.基于压杆屈曲大挠度理论的挂面弯曲折断分析与验证［J］.中国粮油学报，2010，25(8):117-122，128.Jiang Song，Liu Ruixia，Chen Zhangyao，et al.Bending fracture analysis and experimental verification of dry noodles based on large deflection theory of compressive rod buckling［J］.Journal of the Chinese Cereals and Oils Association，2010，25(8):117-122，128.(in Chinese)

［11］范钦珊，王杏根，陈巨兵，等.工程力学实验［M］.北京:高等教育出版社，2006:163-165.

［12］姜 松.基于压杆大挠度理论的挂面弯曲折断分析及测定仪的研制［D］.镇江:江苏大学食品与生物工程学院，2009.

［13］姜 松，朱美如，曾昕鑫，等.基于压杆后屈曲的直条型通心面力学质地［J］.食品科学，2012，33(23):83-87.Jiang Song，Zhu Meiru，Zeng Xinxin，et al.Analysis of mechanical texture of straight thread-like pasta based on compressive rod post-buckling［J］.Food Science，2012，33(23):83-87.(in Chinese)