一种快速比对非编码RNA序列-结构的算法

宋 佳，许 力，孙 洪

(1.浙江大学电气工程学院，浙江杭州310027;2.苏州市职业大学电子信息工程学院，江苏苏州215104)

序列比对是分子生物学研究的基础和重要手段之一.相似的序列通常具有相近的功能或显示较高的同源性，因而可以为生物学研究提供重要的信息.目前，对于DNA和蛋白质序列，已有大量经典的序列比对方法和软件被开发出来，如 BLAST，ClustalW，Muscle等.近年来，也有很多基于隐马尔科夫模型［1］(hidden Markov model，HMM)的方法被提出，并取得不错的效果.但是，对于RNA序列的分析和研究则非常滞后，这是因为最初RNA仅仅被看作DNA基因和蛋白质之间的被动信使，通常被描述为一条线性的无结构序列，除了它所编码的氨基酸序列外并不使人感兴趣.然而，20世纪80年代中期，生物学家发现存在许多非编码RNA(noncoding RNA，ncRNA)，它们具有高级的三维结构，其中一些甚至能催化生化反应.之后的很多研究也表明，非编码RNA在基因调控，染色体的复制和RNA修饰［2-3］等生物过程中都起着重要的作用.对非编码RNA的研究开始得到人们的关注，并逐渐成为生物学研究的新热点.一个非编码RNA分子的生物学功能主要由其二级结构决定，很多同源的非编码RNA序列本身的相似度很低，却具有相同或相似的二级结构.这使得对非编码RNA的序列分析比蛋白质或DNA的序列分析更为复杂，上述的传统的序列分析工具无法满足对非编码RNA结构特性研究的需求.

目前，生物信息学的研究者们已经开发出了大量用于发现和识别非编码RNA的方法和软件工具［4-7］，其中大部分软件都采用共变模型(covariance mode，CM)对非编码RNA家族的二级结构建模［8］，并通过序列结构比对来确定给定的序列片段是否属于这个非编码RNA家族.与隐马尔科夫模型类似，共变模型主要描述基因家族的序列中每一个单个位置或组成一个碱基对的一对位置中所含核苷酸的统计分布.因此，共变模型能够同时精确地描述非编码RNA家族的一级序列和二级结构.单条序列和单个非编码RNA家族的共变模型之间的比对可以通过动态规划算法［1］来计算.

计算最佳序列结构比对的动态规划算法所需的计算时间为O(KL3)，其中L为序列中核苷酸的数量，而K则为共变模型中所含的状态的个数.K通常与它所描述的非编码RNA家族中的序列长度成正比.不难看出，上述算法所需的计算时间随所搜索的非编码RNA的序列长度的增加而迅速增加.由于基因组序列通常包含数量巨大的核苷酸，用上述算法来搜索较长的非编码RNA非常低效.例如，一个中等大小的基因组包含大约一百万个核苷酸，在这样一个基因组中搜索一个包含三百个核苷酸的非编码RNA可能需要数天的时间.目前，对这一缺陷的主要改进方法包括对数据库序列进行过滤［9］和采用并行方案对动态规划算法实现加速［10］.前者虽然减少了待搜索的序列，但过滤后的剩余序列还是必须应用共变模型完成搜索，耗时问题依然存在.后者需要大规模购置并行计算机系统硬件设备，增加了使用、维护的成本.

文中对传统的共变模型进行改进，加入二级结构中结构单元的长度分布信息，根据各个结构单元长度分布对家族中的序列在进化过程中出现插入和删除的次数进行限定，并用C++编程语言编写一个计算机程序来实现这个方法.

1 模型与算法

1.1 传统的共变模型

共变模型是一种可以描述非编码RNA二级结构的概率模型.图1a是一个非编码RNA家族的结构示例.对于不含伪结的非编码RNA，其结构中的碱基对都是以嵌套(nested)的方式出现，如图1b所示，将配对的碱基用线条相连，则这些线条都不会相互交叉，即其符合回文语言的限制条件.因此，可以将随机上下文无关文法(stochastic context-free grammar，SCFG)应用到非编码RNA的二级结构上，从一组相关的非编码RNA序列之间的多序列比对和一致结构中构建共变模型.从数学的角度来看，共变模型和SCFG是等价的.

图1 RNA家族结构示例及配对的碱基

建成的共变模型是状态的一个有向图.它包括K个不同的状态、状态间的连接关系以及每一个状态对应的字符生成概率ek和状态转移概率tk.每个状态信息中包括当前状态的类型、编号、父、子状态的数量及编号.图2为共变模型节点图.

图2 共变模型节点

如图2 所示，状态的类型有7 种:P，L，R，D，S，B和E，依次表示匹配、左生成、右生成、删除、开始、分叉和结束状态.字符生成概率值描述了每个核苷酸或碱基对出现在该位置的概率值.状态转移概率值则描述与之对应的转移发生的概率.

因为共变模型与SCFG等价，单个序列和一个家族的共变模型之间的最优比对可以通过基于SCFG理论模型的标准比对算法CYK(Coche-Younger-Kasami)实现.算法的输入为一条长度为L的非编码RNA序列x=x1x2…xL和一个共变模型.CYK算法的核心是不断地迭代计算一个截面为三角形的三维动态规划矩阵(如图3所示)，动态规划矩阵共有K层，每一层都对应模型中的一个状态.用i，d，k标注动态规划矩阵，其中d是子序列的长度，且d≤D.迭代公式如下(1≤i≤d+1，0≤d≤L，1≤k≤K):

式中:S(k)∈{B，S，D，P，L，R，E}，表示当前状态的类型;γ(i，d，k)为以i结尾且长度为d的子序列与共变模型k状态比对的最优对数几率得分;C(k)为当前状态的子状态集合;y为当前状态的某个子状态;ek和tk分别代表当前状态下的字符生成概率和子状态转移概率;x(i+1-d)为左生成字符;x(i)为右生成的字符.

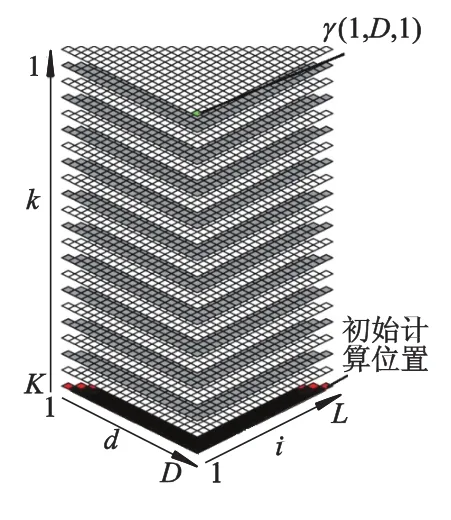
图3 CYK/inside算法三维动态规划矩阵的计算过程

如图3所示，CYK算法从三维矩阵最下层的初始计算位置开始，沿对角线按照波前顺序进行计算.每层元素的计算启动前，首先判断共变模型中当前状态层的类型，根据当前状态类型选择对应的一个公式执行.当下层所有元素计算完毕后再计算上一层的元素.计算过程由下至上逐层推进，直到矩阵最上层中的所有元素算完.此时元素γ(1，L，1)的值就是最终比对分值，它代表该序列与当前RNA家族的相似度.

在上述计算过程中，需要将序列L的所有长度在D以内的衍生子序列都分别与共变模型进行比对.因此，如果能减少衍生子序列的数量，可以显著地降低计算时间.同时，传统共变模型允许比对中的任意位置出现任意长度的插入或删除，如果可以在构建模型时对插入和删除的发生进行约束，就可以减少共变模型中的状态数，进一步降低CYK算法的计算时间.

1.2 改进的共变模型

近年来，对Rfam数据库中非编码RNA家族的研究表明，将一条家族成员的RNA序列与该家族的共变模型进行比对，在模型的任何状态，最优比对的子序列长度都与一致结构的长度相差不多［11-12］.以ByeB非编码RNA家族为例，这个家族已被确定的成员有15个，其平均长度约为100.对其构建共变模型，去除S，B，E节点，可以得到一个有88个节点的压缩后共变模型.将所有15条非编码RNA序列按共变模型进行调整后，计算出其与一致结构在每个状态点的子序列长度偏差，结果显示在表1中.为了便于显示，表1中第1列对共变模型中的88个节点按照结构单元进行了分组，结果显示，在各状态，子序列长度与一致结构的长度都基本吻合(没有任何一个长度偏差大于2).在节点88-81，全部成员的子序列长度与一致结构的长度之间都没有偏差，也就是说，对于这8个节点，这些家族序列的最优比对无需进行插入或删除操作.而Rfam数据库中许多其他家族的测试结果显示，从上述例子中得出的结论是普遍适用的.

表1 ByeB家族子序列长度偏差

采用传统的共变模型，在进行动态规划时需要对所有长度在D以内的子序列都分别与共变模型进行比对.以ByeB家族为例，Rfam数据库对其子序列长度上限D取值为150.即在对共类模型中第88个节点计算时，就需比对长度偏差在-1到+149之间的所有子序列.而根据上述ByeB家族的测试结果，这150个搜索点中的149个都毫无价值.

因此，文中改进了传统的共变模型，将RNA家族的二级结构分成若干个基本的结构单元，其中每一个结构单元代表二级结构中的一个茎 (stem)或者一个环(loop).如图4所示，连续堆积的碱基对称为茎，以碱基对为界的单链子序列称为环.每个结构单元都与一对整数相关联，这对整数分别是结构单元的最小长度和最大长度.换言之，将每个结构单元的长度限制在一个区间内.1.3节将详细描述确定结构单元长度区间的方法.除了对结构单元长度的限制以外，结构模型仍然采用共变模型来描述一个非编码RNA的二级结构.

图4 RNA二级结构的基本结构单元

1.3 结构单元长度限制的计算

如上文所述，结构模型中的每个结构单元都与一对整数相关联，这对整数描述了该结构单元在非编码RNA序列中的长度范围.下面介绍该长度范围的计算方法.

首先，给定一组非编码RNA家族中的训练序列，可以为其中每一个结构单元S构建一个隐藏马尔可夫模型M.然后，根据训练序列计算组成S的子序列的平均长度以及其碱基组成.用A表示训练序列中S的平均长度，并根据这个碱基组成来随机生成长度为A的N个子序列.接下来将所有生成的子序列与M进行比对，从而得到N个不同的比对分数.这N个比对分数一起构成一个给定碱基组成所生成的子序列的比对分数分布.根据这个分布，可以计算出这N个比对分数的平均值m和标准偏差d.

下一步进行结构单元S长度的上、下限计算.文中采用了一种方法，可以在计算出上、下限的同时，给出一个置信值p.以序列结构的长度上限为例，计算步骤如下:从L'=L+1开始，使用相同的碱基组成随机生成N个长度为L'的不同的子序列，并分别与M进行比对;通过这些比对可以生成N个比对分数;这N个比对分数组成一个新的分布，计算出其平均值m'.然后，检查这个新分布和前面获得的所有长度为L的子序列的比对分数的分布在统计学上是否有显著差异.为此，比较m和m'的差异是否大于，其中c是一个常数，它的值可以根据统计置信值p计算出.如果m和m'的差异大于则终止以上的步骤，并输出此时的L'作为S的长度的上限.否则，将L'的值递增1，重复以上步骤直至根据L'生成的子序列的得分分布与之前长度为L的子序列的得分分布在统计学上有显著不同为止.同样，序列结构的下限也可以采用类似的方法获取.

1.4 序列结构比对

通过单条RNA序列L与之前构建的RNA家族共变模型M之间的结构比对，可以判定该序列是否属于该家族.结构比对通过CYK算法实现.

如上文所述，根据每一个结构单元的长度限制，可以计算出共变模型中每一个状态所衍生的子序列的长度范围.因此，对改进的共变模型来说，如果状态S(k)不是“分支”态(B)，且其所对应的长度范围是［dmin，dmax］，那么上面的算法只需要对L中所有满足dmin≤d≤dmax的长度为d的子序列完成动态规划的计算过程，所需的计算时间是O((dmax-dmin)L).

如果S(k)是“分支”态，假定它所分出的两个状态所对应的长度范围是［smin，smax］和［lmin，lmax］，那么S(k)所衍生的子序列的长度范围是［smin+lmin，smax+lmax］.对每一个长度位于这个区间的子序列，分支点的可能位置不超过b=min{smax-smin，lmax-lmin}个.因此，可以算出当S(k)是“分支”态时，上面的算法所需的计算时间是O((smax+lmax-sminlmin)bL).如果考虑模型中所有K个状态和它们所能衍生出的子序列的长度范围，并用Δ来表示所有这些长度区间长度的最大值，那么整个动态规划所需的计算时间不超过O(KΔ2L).

对于一个结构单元的长度范围所对应区间的长度值，可以用一个粗略的模型来估算，即假定子序列中每一个核苷酸对比对分数的平均值和方差的贡献都相同且独立于其他核苷酸.用n和δ来表示这两个贡献值，根据前面的讨论，如果结构单元的平均长度为l，则其长度范围中的每一个长度值l'必须满足下式:

由于n，c，δ都是常数，由上式可得结构单元长度范围对应区间的长度不超过.由此可得，如果选取N=l2，则区间的长度是一个常数.

根据上面的讨论，可以得到动态规划所需的时间复杂度，假定模型中含有g个分支状态，则:

因此，动态规划过程所需的计算时间不超过O(Kg2L)，这与传统的共变模型所需的O(KgL3)时间复杂度相比有非常显著的改善.

2 试验结果

文中用C++编写了一个程序来实现上述方法，并在方法的精度和效率上，与其他使用传统共变模型的工具进行了比较.测试数据从Rfam数据库获取，对每个基因组家族，选取最多60个序列，这些序列两两之间的相似度低于种子序列之间最小相似度的80%.将几个来自同一基因组家族的RNA序列插入随机生成的具有相同碱基组成的序列中.然后，应用本算法和一个基于共变模型的搜索算法搜索插入的序列.

为了计算每个结构单元的长度限制，假设每个结构单元的长度构成一个正态分布，选择置信值p=0.01，常数c的取值为 3.0.对几个不同的非编码RNA家族分别进行了测试，并对方法的敏感性和特异性进行了比较.表2列出了本方法和其他基于传统共变模型的搜索算法在敏感性和特异性方面的精度.

表2 本方法与基于CM的搜索算法的敏感性和特异性比较

由表2可见，本方法在所有测试的非编码RNA家族上都能取得与基于CM的搜索算法相近或更高的精确度，对Purine家族的搜索敏感性甚至高于基于CM的搜索算法.这个测试结果间接表明，本方法尽管使用了近似的方法大大减少了在序列-结构比对中需要搜索的可能构型的数目，但对比对的精确度没有产生严重的负面影响.

表3列出了本方法和其他基于传统共变模型的方法的计算时间.同样不难看出，对于所有测试的非编码RNA基因家族，本方法的计算速度都明显优于其他基于传统共变模型的方法.特别是对Lin-4的测试结果表明，本方法在实现与基于传统共变模型的方法相同敏感性和特异性的搜索精度的同时，将搜索的速度提高近90.76倍.

表3 搜索所有非编码RNA基因家族所需的计算时间比较

3 结论

文中提出一种比对非编码RNA序列-结构的新算法，结论如下:

1)根据结构单元的长度限制，计算出共变模型中每个状态衍生的子序列的长度范围，从而减少了衍生子序列的数量，与传统共变模型的非编码RNA序列搜索算法相比较，在同样的精确度下有更高的比对速度.

2)到目前为止，本方法还只能用于搜索不含有伪结的非编码RNA.伪结因为包含交叉茎，其二级结构的模型建立更加困难.因此，开发能够对含有伪结的非编码RNA建模和搜索的方法，是笔者未来的一个工作方向.

References)

［1］杨卫国，纪灵军，孙 杰.关于m重隐非齐次马尔可夫模型的混合性［J］.江苏大学学报:自然科学版，2009，30(6):645-648.Yang Weiguo，Ji Lingjun，Sun Jie.Mixing property ofmth order hidden nonhomogeneous Markov models［J］.Journal of Jiangsu University:Natural Science Edition，2009，30(6):645-648.(in Chinese)

［2］Mayer C，Neubert M，Grummt I.The structure of NoRC-associated RNA is crucial for targeting the chromatin remodelling complex NoRC to the nucleolus［J］.EMBO Reports，2008，9(8):774-780.

［3］Zhang B H，Pan X P，Cobb G P，et al.MicroRNAs as oncogenes and tumor suppressors［J］.Developmental Biology，2007，302(1):1-12.

［4 ］Zhang Baohong，Pan Xiaoping，Stellwag Edmund J.Identification of soybean microRNAs and their targets［J］.Planta，2008，229(1):161-182.

［5］Jacob A，Buhler J D，Chamberlain R D.Accelerating Nussinov RNA secondary structure prediction with systolic arrays on FPGAs［C］∥Proceedings of the IEEE International Conference on Application-Specific Systems，Architectures and Processors.Belgium:IEEE，2008:191-196.

［6］Markham N R，Zuker M.UNAFold:software for nucleic acid folding and hybridization［J］.Methods in Molecular Biology，2008，453:3-31.

［7］WJ Anderson J，Tataru P，Staines J，et al.Evolving stochastic context-free grammars for RNA secondary structure prediction ［J］.BMC Bioinformatics，2012，doi:10.1186/1471-2105-13-78.

［8］Andersen E S.Prediction and design of DNA and RNA structures［J］.New Biotechnology，2010，27(3):184-193.

［9］Bradley R K，Pachter L，Holmes I.Specific alignment of structured RNA:stochastic grammars and sequence annealing［J］.Bioinformatics，2008，24(23):2677-2683.

［10］Sükösd Z，Knudsen B，Værum M，et al.Multithreaded comparative RNA secondary structure prediction using stochastic context-free grammars［J］.BMC Bioinformatics，2011，12，article number:103.

［11］Gardner P P，Daub J，Tate J G，et al.Rfam:updates to the RNA families database［J］.Nucleic Acids Research，2009，doi:10.1093/nar/gkn766.

［12］Sempere L F，Sokol N S，Dubrovsky E B，et al.Temporal regulation of microRNA expression in drosophila melanogaster mediated by hormonal signals and broadcomplex gene activity［J］.Developmental Biology，2003，259(1):9-18.