基于改进型多目标粒子群算法的晶圆制造系统瓶颈工作站调度

周炳海，胡新宇，孙 超

(同济大学机械与能源工程学院，上海201804)

如何解决延时生产与顾客准时交货之间的矛盾，不断提高产能，降低制造周期，是目前半导体制造企业面临的主要问题.半导体制造系统中，瓶颈制约着整个系统的产出，必须最大限度地利用瓶颈资源［1］.因此，如何调度瓶颈工序，使瓶颈工作站避免出现空闲现象，保证系统产出率，对提高半导体晶圆制造系统的效率具有重要意义.

瓶颈调度属于NP难问题，目前对于该调度研究，国内外的研究方法大致可以归为:通过投料策略调控瓶颈区、基于启发式规则、基于 DBR(drum，buffer and rope)理论、基于智能算法［2］.随着晶圆重入流增加，整个制造过程复杂度增加，投料策略对瓶颈工作站的调控能力大幅降低［3］.启发式规则以其简单、快速的优势得以在半导体晶圆制造系统中被广泛应用，但由于其无法进行优化，解的质量不高.例如，Wang Zuntong等［4］采用启发式派工规则赋予瓶颈前待加工工件优先级，进行瓶颈工作站调度.基于DBR理论的晶圆制造系统调度方法通常是结合晶圆制造系统多重入特点与DBR思想，基于“层”对瓶颈区进行调控，此方法主要关注瓶颈的利用率，而没有考虑瓶颈工作站的优化调度问题.例如，Cao Zhengcai等［5］通过保证一定的“层”装载量以避免瓶颈工作站空闲，进而结合缓冲大小与“层”装载量进行瓶颈工作站调度.一些学者也尝试用智能算法来调度晶圆制造系统瓶颈工作站.Yang Fengcheng等［6］研究了基于时间窗和遗传算法的晶圆制造系统瓶颈工序光刻区的多目标调度问题，但该方法是通过赋予4个目标一定的权重，将其转化成单一目标，简化了调度问题.

为了能有效解决半导体生产系统瓶颈工作站多目标调度问题，文中将引入多目标粒子群优化(multi-objective particle swarm optimization，MOPSO)算法，通过改进速度和位置的更新机制，对陷入局部最优的粒子进行交叉操作，设计用于瓶颈工作站调度的改进型多目标粒子群算法.

1 问题描述

半导体晶圆制造系统规模庞大，具有多重入性，一个晶圆为了完成所有的电路层，必须多次访问光刻工作站.光刻工作站在晶圆制造系统中利用率最高，为瓶颈工作站.为有效地描述基于改进型多目标粒子群算法的半导体晶圆制造系统瓶颈工作站调度，做如下定义和假设:① 晶圆在每个电路层的最后一道工序是光刻，访问瓶颈工作站多少次，就意味着晶圆完成加工需经历多个电路层;② 晶圆按批(lot)进行加工;③ 生产多种晶圆，每种晶圆有固定加工路径，每条路径上串联着多个工作站，每个工作站中有若干台平行机;④同一工作站中的平行机的平均有效处理时间相同，且已知;⑤ 晶圆完成所有工序的总加工时间已知，晶圆的交货期已知;⑥ 假设晶圆到达系统服从泊松分布;⑦系统输入的晶圆数量无限，同时成批到达，即系统输入缓冲区无限;⑧非瓶颈工作站按先进先出原则(first in first out，FIFO)进行加工.

2 调度建模

为解决顾客准时交货与企业自身延时生产之间的矛盾，将准时交货要求映射为瓶颈工作站平均加权提前/拖期时间，将快速生产要求映射为瓶颈工作站流程时间，从而确定了优化目标为最小化瓶颈工作站平均加权提前/拖期时间和最小化瓶颈工作站流程时间.于是，得到如下数学规划模型:

式中:i为晶圆种类;w为工作站编号;k为设备编号;hij为第i种晶圆第j次访问瓶颈工作站;Qi为第i种晶圆的权重;I为晶圆总数;Tdhij为第i种晶圆在第j个电路层上瓶颈工序交货期提前/拖期时间;Chij为第i种晶圆在第j个电路层上瓶颈工序完工时间;ti为第i种晶圆到达系统的时刻;Eijwk为第i种晶圆在第j个电路层上工作站w中设备k上的完工时刻;Sijwk为第i种晶圆在第j个电路层上工作站w中设备k上的开始加工时刻;tew为工作站w中机器的有效处理时间;Xijwk为1表示第i种晶圆在第j电路层上工作站w中设备k上加工，为0表示其他情况;Rijfgwk为1表示第i种晶圆在第j电路层和第f种晶圆的第g个电路层均需经过工作站w中设备k，且前者的加工优先后者，为0表示其他情况.式(1)-(2)为目标函数;式(3)表示对于某一晶圆，其下一工序必须在上一工序全部完工后才能开始;式(4)表示工作站w中设备k不能同时加工2种晶圆;式(5)表示晶圆在工作站w中设备k上的完工时刻与其开始时刻之差不能小于其所需加工时间;式(6)表示晶圆在工作站w上的加工由该工作站中的唯一一台设备独立完成.

3 算法构建

为求解上述多目标优化问题，设计了一种改进型多目标粒子群算法.算法的核心思想如下:① 运用排列组合编码方式表达粒子;②由于基本粒子群(particle swarm optimization，PSO)算法的位置及速度更新公式难以表述离散域问题，采用交换子及交换序概念，设计位置及速度的更新机制;③引入约束支配概念［7］，进行约束处理;④ 基于 Pareto支配关系，采用排除法构造非支配集，用于存放非支配粒子;⑤采用文献［8］中ε支配关系构造并更新外部集，用于存放全局极值;⑥ 文献［9］指出，粒子群算法在局部最优值附近收敛缓慢，容易陷入局部最优.为减少粒子早熟现象的发生，加强粒子多样性，提高IMOPSO的全局搜索能力，对陷入局部最优的粒子设计交叉操作，克服早熟收敛问题［8，10］.图1描述了IMOPSO算法的组件及每个组件的操作及组件之间的相互关系.

图1 改进型多目标粒子群算法示意图

改进型多目标粒子群算法的具体步骤归纳如下.

1)初始化粒子群，种群大小为P.

①在可行域内随机初始化粒子群中粒子的位置向量Ya，初始化交换序，即粒子的速度向量Va.其中，Ya的编码采用排列组合方式.即若瓶颈工作站前有n个待加工晶圆，则Ya为{1，2，…，n}的一个排列.Va初始化为一个交换子，即在(1，2，…，n)中随机生成2个不同的元素，构成一个交换子.

② 设置惯性权重ωd及学习因子α，β.ωd采用如下惯性因子:

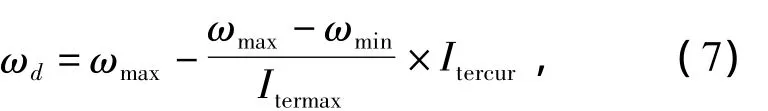
式中:ωmax，ωmin分别为惯性权重最大值及最小值;Itermax，Itercur分别为最大迭代次数及当前迭代次数.

③粒子a的个体极值Pbesta和全局极值Gbesta均初始化为粒子本身.

2)求各粒子的适应度函数值f1(a)，f2(a).

3)更新非支配集.非支配集的更新采用基于Pareto支配关系的排除法.具体思想如下:将粒子群体中的每个个体a依次与非支配集(初始化为空集)中的个体e比较.如果aPareto支配e，将e从非支配集中剔除.如果a不被非支配集中任意一个个体支配，则将a并入非支配集.当非支配集为空集时，直接将a并入其中.

4)更新个体极值.基于竞争选取原则进行个体极值的更新.具体思想如下:若当前粒子a支配Pbesta，用a更新Pbesta;若Pbesta支配a，则个体极值不变;若两者互不支配时，以50%的概率进行替换.

5)更新外部集.采用外部集保存当前找到的非支配解集，将ε支配概念用于更新外部集，以使算法保持较好的分布性.其中，外部集即为粒子全局极值的候选集，而外部集保留的最终解即为算法求解的结果.具体思想如下:若某个非支配粒子不被外部集中任一粒子ε支配，则将其并入外部集;若外部集中某一粒子被新并入的非支配粒子ε支配，则将该粒子剔除.

6)更新全局极值.利用外部集是粒子全局极值的候选集合这一概念，进行全局极值的更新.具体思想如下:对于粒子a，从外部集中随机选取一粒子，若该候选粒子支配a的全局极值Gbesta，则将该候选粒子作为a的新全局极值;若Gbesta支配该候选粒子，则全局极值不变;若两者互不支配，则以50%的概率进行替换.

7)计算粒子的停滞代数Sa，若Sa大于或等于该粒子的健康度阈值Ha，表明该粒子出现早熟现象，转到步骤8)，进行交叉操作;否则，转到步骤9).

8)交叉操作.将出现早熟现象，即陷入局部最优的粒子a与外部集中随机选取的较优粒子e进行交叉操作，交叉后a的停滞代数更新为0.交叉方法具体思路如下:对于粒子a和e的位置向量Ya，Ye，在其位置元素总数n中产生一个随机数q，保留Ya中的前q个元素，将Ye中后n-q个元素插入Ya中相应的n-q个位置，而Ya中其余元素则顺序后延，则生成一个新的位置;然后保持新插入元素不变，剔除中其余位置重复出现的元素，则得到粒子a的更新后的位置.具体实现步骤如图2所示(假设n=9).

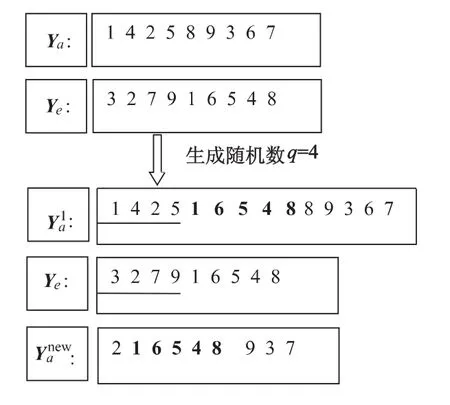
图2 交叉操作

9)分别按式(8)，(9)更新粒子的速度及位置，转至步骤2)直至满足中止条件(迭代次数达到最大迭代次数)退出.

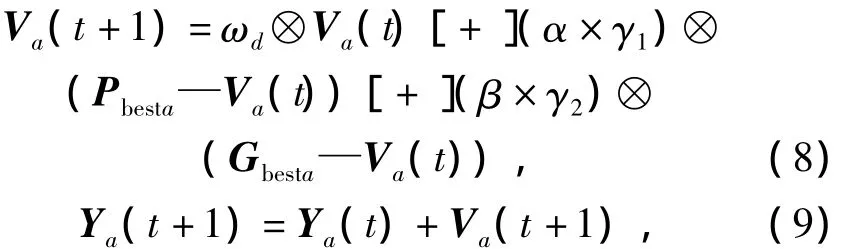
式中:γ1，γ2为［0，1］上的随机数.

上述表示式中，“⊕”表示参与运算的交换子之间的作用顺序.则粒子速度即为多组交换子的“⊕”运算;“［+］”表示为两个速度各自的交换子按序作“⊕”运算;“—”表示了由位置Ya变换到位置Ye所需的一组交换子.“+”表示是将速度中各项交换子按序作用于位置.常数r(r∈［0，1］)与速度 Va“⊗”运算关系如下:先计算r×‖Va‖(其中，‖Va‖表示速度Va中交换子的个数)，且对该结果向下取整，记为‖‖;由前‖‖个交换子构成新的速度;如果‖＞1，则r⊗Va=，否则，在Ya中随机选择两个元素，构成一个交换子，从而生成速度，则

4 试验分析

为有效评价文中设计的改进型多目标粒子群算法，进行如下仿真试验设计:①以经典的Mini-Fab模型为原型，根据本算法假设条件，对Mini-Fab进行适当改变，形成如下仿真模型:晶圆制造系统有5个工作站，各工作站中有2-3台机器，其中光刻工作站有2台机器;晶圆种类为3种，各晶圆经历的电路层层数均为2层;晶圆以lot进行加工，不考虑batch处理.②晶圆到达系统服从参数λ=5的泊松分布;非瓶颈工作站调度采用FIFO规则.③ 运用IMOPSO算法对瓶颈工作站调度时，参数设置如下:种群规模P=30，最大迭代次数Itermax=50，粒子健康度阈值Ha=5，惯性权重 ωmax=1.0，ωmin=0.6，学习因子 α =0.8，β =0.8.④ 仿真试验硬件为主频 2.13 GHz、内存4 GB的PC机，采用C++编程语言进行仿真程序编程.

4.1 仿真分析

t=19.28 s时刻进行瓶颈调度时，瓶颈工作站前有7 个待加工晶圆，将其分别标记为l1，l2，l3，l4，l5，l6，l7.结合文献［11］对 MOPSO 算法的应用及文献［10］对PSO算法粒子的表达及交叉设计，通过200次运行，与未对出现早熟现象粒子进行交叉操作的MOPSO算法进行比较，分析IMOPSO算法性能.

1)分别统计IMOPSO，MOPSO算法中出现率大于等于40%的调度方案，结果如表1，2所示.

表1 IMOPSO运行结果统计

表2 MOPSO运行结果统计

统计IMOPSO算法运行结果，根据表1所罗列的调度方案的两个目标值与该算法趋近稳定后两个目标值均值的偏差，可以得到如表3所示的结果.

由表3可以看出，上述IMOPSO算法中出现次数较多的调度方案的两个目标值与该算法趋近稳定后目标值均值的偏差较小，这说明该算法所输出的结果相对较优，Pareto前沿的质量相对较高，能获得准时交货与快速生产两者的较优配合.

表3 IMOPSO目标值分析 %

由表1可以看出，上述IMOPSO算法所输出的结果相对较稳定.准时交货与快速生产两者达到较优组合的晶圆排序(l5，l4，l6，l1，l2，l7，l3)与(l4，l5，l2，l6，l3，l7，l1)在200次运行中出现率分别为85%和78%，这表明运用该算法进行瓶颈调度时可以较好地解决准时交货与延时生产要求间的矛盾.由表1及表2可以看出，IMOPSO比MOPSO有更好的性能，拥有更优的Pareto最优解集，在进行瓶颈调度时更稳定.

2)IMOPSO，MOPSO算法外部集中两个目标函数的演化曲线如图3所示.其中曲线代表每代外部集解群体的平均目标值.

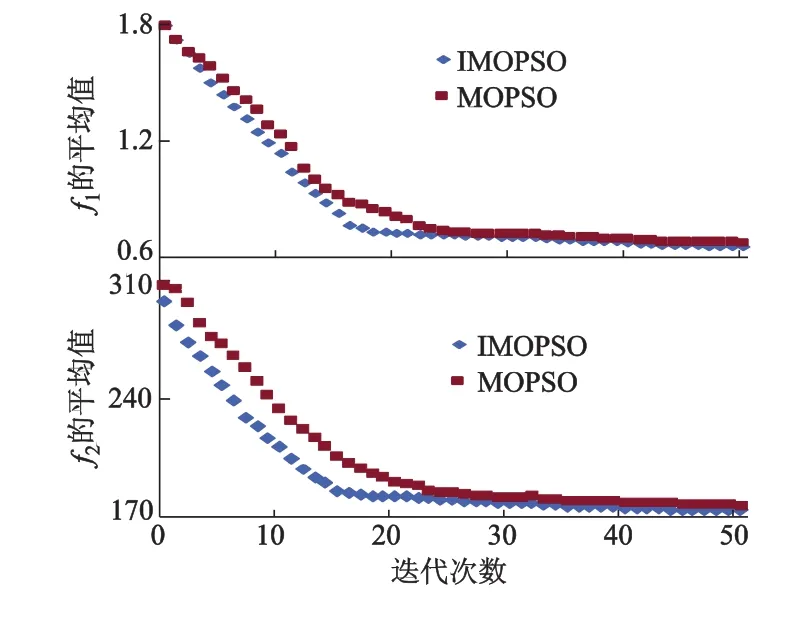
图3 目标函数f1和f2的Pareto最优演化过程

由图3可以看出，随着算法的不断演化，曲线不断下降，外部集解群体的目标平均值越来越趋于Pareto最优和稳定，相比之下，IMOPSO算法的收敛速度更快.

3)分别统计IMOPSO，MOPSO算法下200次运行的时间，记录最好结果、最差结果及平均结果，见表4.

表4 IMOPSO，MOPSO算法运行时间统计

由表4可知，IMOPSO算法在运行时间上稍逊于MOPSO算法，但其仍能在连续200次计算中较快速地搜索到相对稳定的Pareto最优解群体，完成对瓶颈区调度结果的输出.

4.2 系统性能分析

为了进一步验证文中提出的改进型粒子群算法能有效调度瓶颈工作站，在解决准时交货与延时生产间矛盾的同时，能进一步降低制造周期，获得相对较高的系统产能及合理的在制品水平，文中选用瓶颈区FIFO调度规则与本算法进行系统绩效分析，其中运用本算法进行瓶颈调度时，采取从外部集中随机选取某一调度方案的规则，用以确定瓶颈工作站晶圆的加工顺序.

系统绩效指标为产能(throughput，TH)及在制品(work in process，WIP)，分别以QTH及QWIP表示.根据Little定理，QTH一定时，QWIP增加，制造周期(cycle time，CT)会相应增加.因此，系统最佳目标亦是取得较高QTH和较低QWIP，从而得到二者最佳配合.整个仿真试验时间是6个月，数据选取自后4个月.

试验结果如表5所示，表中分别记录了两个算法的系统产能QTH与QWIP的最佳值、最差值及平均值.其中，每个数据都是经过10次仿真试验得到的.

表5 QTH，QWIP的比较结果

根据10次仿真得到的系统绩效指标值QTH和QWIP，分别绘制两个算法下QTH，QWIP关于仿真次数的趋势图，见图4.

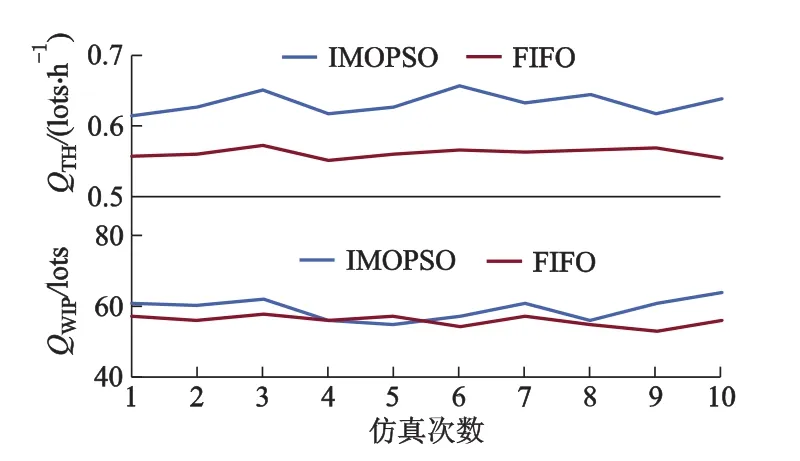
图4 QTH和 QWIP趋势

由表5及图4可见，运用IMOPSO算法进行瓶颈工作站调度比用FIFO调度能获得相对更高的系统产能.虽然前者的系统QWIP值基本都比后者高，但是前者相对后者的QWIP值增幅却远小于其QTH的增幅，因此采用文中提出的改进型多目标粒子群算法对瓶颈工作站进行调度时，不仅可以得到较高的系统产能，而且可以得到相对合理的在制品，即相对合理的制造周期，这说明本算法是有效的.

5 结论

1)通过改进速度和位置的更新机制，设计交叉操作用于克服粒子的早熟现象，构建了改进型多目标粒子群算法，用于瓶颈工作站调度.

2)试验分析表明，文中提出的改进型多目标粒子群算法所输出的Pareto前沿的质量相对较高，算法稳定性较好.随着算法的不断演化，外部集解群体的目标平均值越来越趋于Pareto最优和稳定，收敛速度较快.算法运行时间较短，能较快速地搜索到相对稳定的Pareto最优解群体.在较好解决企业延时生产要求与客户准时交货要求间矛盾的同时，可以取得较高的系统产能及相对合理的在制品水平，达到二者的较佳配合.

3)调度模型和算法可为半导体晶圆制造系统瓶颈工作站调度研究提供借鉴和指导作用.

References)

［1］Tsou C M.On the strategy of supply chain collaboration based on dynamic inventory target level management:a theory of constraint perspective［J］.Applied Mathematical Modeling，2013，37(7):5204-5214.

［2］Tang Chunhui，Qian Yuliang，Zhu Jun，et al.A scheduling method in semiconductor manufacturing lines based on genetic algorithm and simulated annealing algorithm［C］∥Proceeding of the2010International Conference on Information，Networking and Automation.Kunming:IEEE Computer Society，2010，doi:10.1109/ICINA.2010.5636524.

［3］Bahaji N，Kuhl M E.A simulation study of new multiobjective composite dispatching rules，CONWIP，and push lot release in semiconductor fabrication［J］.International Journal of Production Research，2008，46(14):3801-3824.

［4］Wang Zuntong，Wu Qidi，Qiao Fei.A lot dispatching strategy integrating WIP management and wafer start control［J］.IEEE Transactions on Automation Science and Engineering，2007，4(4):579-583.

［5］Cao Zhengcai，Peng Yazhen，Wang Yongji.A drumbuffer-rope based scheduling method for semiconductor manufacturing system［C］∥Proceedings of the2011IEEE International Conference on Automation Science and Engineering.Trieste，Italy:IEEE Computer Society，2011:120-125.

［6］Yang Fengcheng，Kuo Chunnan.A time window rolling and GA-based method for the dynamic dispatching problem in photolithography area［C］∥Proceeding of the2010 40th International Conference on Computers and Industrial Engineering.Awaji，Japan:IEEE Computer Society，2010，doi:10.1109/ICCIE.2010.5668209.

［7］Vergidis K，Saxena D，Tiwari A.An evolutionary multiobjective framework for business process optimisation［J］.Applied Soft Computing Journal，2012，12(8):2638-2653.

［8］Chen Yu，Zou Xiufen，Xie Weicheng.Convergence of multi-objective evolutionary algorithms to a uniformly distributed representation of the Pareto front［J］.Information Sciences，2011，181(16):3336-3355.

［9］张鼎逆，刘 毅.基于混合粒子群法的RLV上升段轨迹优化［J］.江苏大学学报:自然科学版，2013，34(1):54-59.Zhang Dingni，Liu Yi.RLV ascent trajectory optimization based on hybrid PSO method［J］.Journal of Jiangsu University:Natural Science Edition，2013，34(1):54-59.(in Chinese)

［10］杨虎林，闭应洲，王仁民，等.基于改进粒子群优化算法求解带时间窗的车辆路径问题研究［J］.广西师范学院学报:自然科学版，2011，28(4):98-102.Yang Hulin，Bi Yingzhou，Wang Renmin，et al.An improved particle swarm optimization algorithm for vehicle routing problem with time window［J］.Journal of Guangxi Teachers Education University:Natural Science Edition，2011，28(4):98-102.(in Chinese)

［11］Zizler E.Evolutionary algorithms for multiobjective optimization:methods and applications［D］.Zurich:Swiss Federal Institute of Technology，1999.