空间超高速撞击碎片云前端速度的预测模型

安 凯

（山东航天电子技术研究所，烟台 264003）

0 引言

碎片云轴向最大速度（以下称前端速度）是对航天器内部仪器设备毁伤程度评价的一个重要因素。仪器设备的外壳能否被击穿以及击穿面积的大小都与碎片云的前端速度密切相关，而前端速度又与撞击航天器外壳的空间碎片的速度大小以及航天器外壳的结构、材质与厚度等多种因素有关[1-8]。由于超高速碰撞发生在空间，要真实地获取碎片云 前端速度极其困难，因此地面模拟试验便成为获取碎片云前端速度的主要途径。地面模拟试验主要手段是用二级轻气炮发射弹丸撞击靶板。影响碎片云前端速度的因素很多，至少包括弹丸直径、弹丸速度和靶板厚度，即建立的碎片云前端速度模型至少应是一个三元函数。而多元函数的建模不仅需要更多的试验样本，运算的复杂度也更高，因此许多研究者采用无量纲化的方法，将多元函数建模问题转换为一元函数建模问题。例如文献[4]和文献[5]将无量纲化变量V1/V0作为无量纲化变量t/D的函数，通过建立V1/V0的模型间接获得V1的模型，则无量纲化模型的形式为V1/V0=[a(t/D)+b]c，式中：V1是碎片云的前端速度；t是靶板厚度；D是弹丸直径；V0是弹丸撞击速度；a、b和c是拟合样本数据时的待定系数[8]。

无量纲化模型的一个明显缺陷是，在t/D一定时V1/V0只能是一个常数。而文献[3]中的试验数据显示，当t/D=0.026，V0分别为4.67 km/s、6.54 km/s、6.7 km/s 时，V1/V0分别为0.985、1.032、1.030。可见这种“无量纲化”的方法与试验数据存在一定差异，其原因就是独立变量个数太少。本文将建立包含弹丸直径、弹丸速度和靶板厚度3 个变量的碎片云前端速度三元函数，然后利用多元函数的拟合方法建立碎片云前端速度的预测模型。

1 试验及相关数据

1.1 试验数据

本文采用二级轻气炮发射球形弹丸进行超高速撞击试验，弹丸材料为2017-T4 铝合金，靶板材料采用6061-T6 单层铝合金板（600 mm×600 mm）。试验进行了6 次，并采用闪光X 射线高速摄影机全程拍摄撞击过程。试验数据见表1。

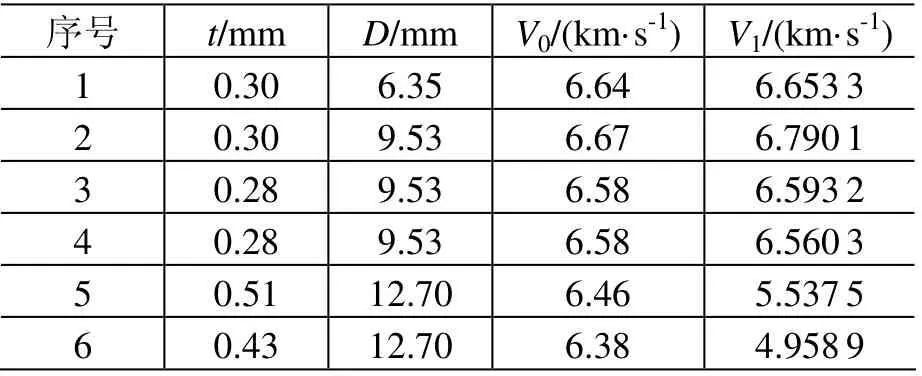
表1 6 次超高速撞击试验数据Table 1 Data of six hypervelocity collision tests

1.2 相关数据

文献[3]给出了一组二级轻气炮的超高速撞击试验数据，试验所采用的2017-T4 铝合金球形弹丸的直径分别为6.35 mm、9.53 mm 和12.70 mm，6061-T6 铝合金单层靶板的厚径比t/D及试验数据见表2[3]。

由表2的数据计算可得出V1和t，最终获得建模所需要的4 个独立变量（t、D、V0、V1），见表3。在用表2中的样本序号数据计算所得结果填入表3中时，只是将表2中序号分别为4、9 和16 的样本数据计算结果依次排在表3的最后，其余样本数据及计算结果的相对排序维持不变。

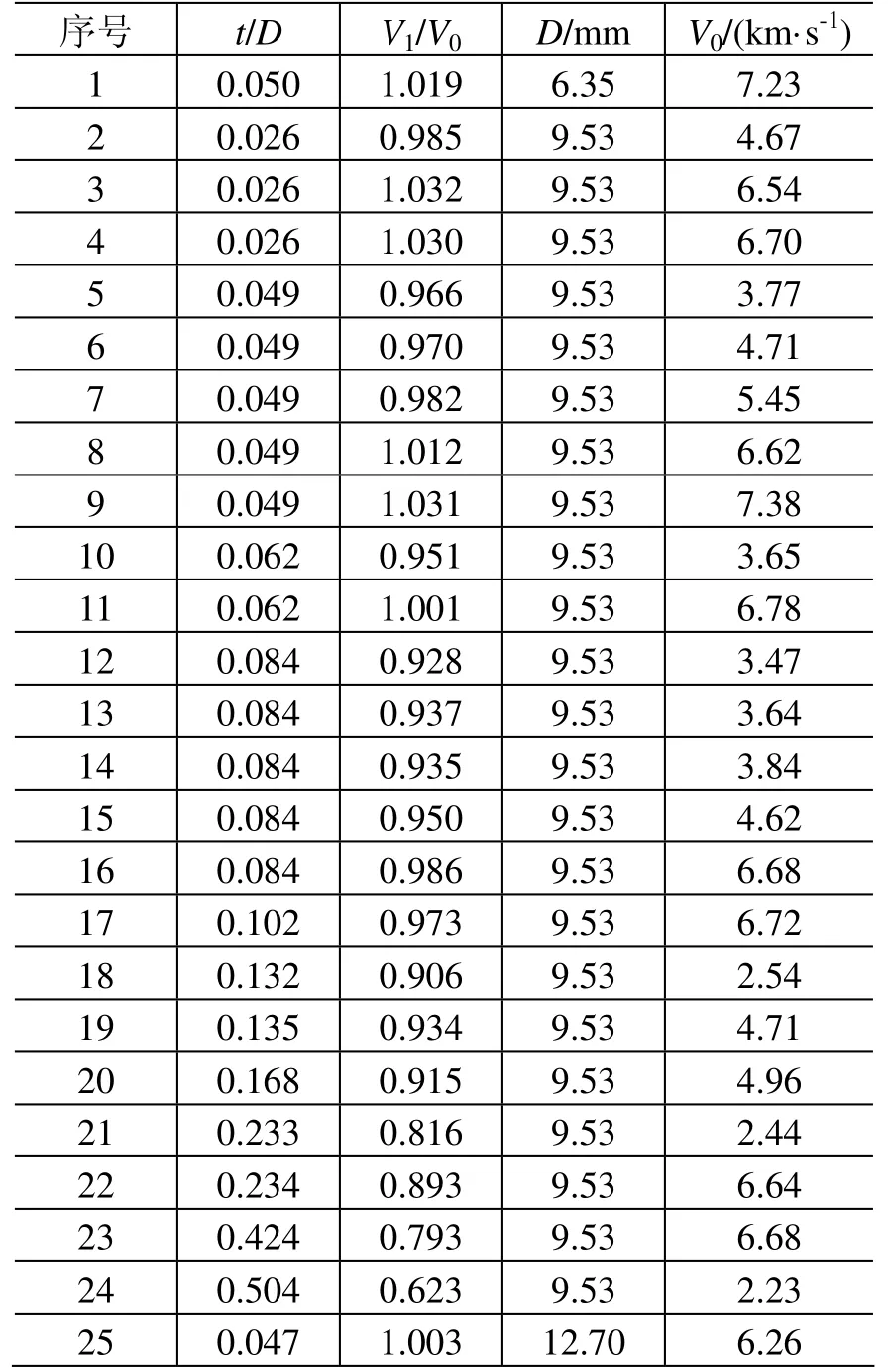
表2 超高速撞击试验数据Table 2 Data of the hypervelocity collision test

表3 建模变量数据Table 3 Variables for model setting

续表3

考虑到模型预测精度的验证问题，将试验数据分为样本数量不同的两组，样本较多的一组用来建立拟合模型，以保证用于建模的样本中t/D有更多的值；而样本较少的一组用来验证所建立的模型。因此，选择表3中的最后3 个样本作为验证样本；用表3中的前22 个样本以及表1的全部6 个样本来建立拟合模型。

2 碎片云前端速度的模型及预测

2.1 前端速度模型的建立

在弹丸和靶板的材料一定时，碎片云前端速度V1主要取决于靶板材料厚度t、弹丸直径D和撞击速度V0，因此V1=f(t,D,V0)。

建立三元函数f(t,D,V0)的数值模型的关键是建模方法的选择。神经网络建模法虽然已经被证明具有很好的逼近效果，并在许多建模问题中得到应用[9]，但所建模型的学习时间太长，参数较多，改变弹丸和靶板材料后重新建模十分困难。而采用多元多项式逼近建模方法，只要函数在某一点展开的Taylor 级数足够高，就可以无限逼近原函数。

一个三元函数的二阶Taylor 展开式可以表示为

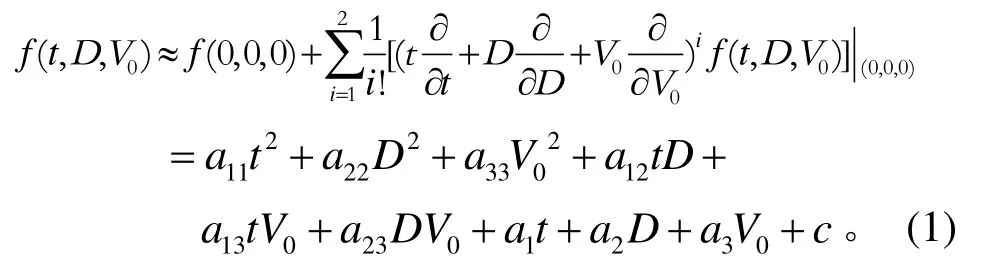
式中：aij，ai是f(t,D,V0)的二阶Taylor 展开式的系数；c=f(0, 0, 0)。

式(1)可改写成矩阵形式为

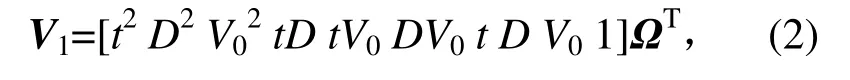
即称之为三元二阶多项式模型（以下简称多项式模型）。其中Ω=[a11a22a33a12a13a23a1a2a3c]。

分别以ti，Di，V0i和V1i(i=1,2,…,n)表示第i个试验数据，并将这些数据代入式(2)得到：

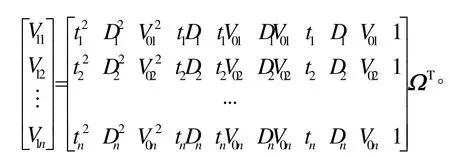
记Y=[V11V12…V1n]T；

则有Y=AΩT。根据最小二乘法原理，使拟合的方均根误差达到最小的解[10]为

为保证式(3)在det(Ω)=0 时仍然有解，不妨取ΩT=A+Y，其中A+表示矩阵A的广义逆矩阵[8]。

式(2)为碎片云前端速度模型，是具有3 个独立变量的函数。将表1和表3中的前22 个数据样本代入该模型后得ΩT=[-0.0027 -0.0312 0.0124 0.9080 -0.0480 -0.0222 -8.6977 0.3590 1.1430 -0.5494]。

为了直观地了解碎片云前端速度模型的拟合效果，图1依次绘出了表1和表3的前22 个建模样本点的前端速度，以及由碎片云前端速度模型计算得到的相应的前端速度的拟合值，可以看出绝大多数的拟合点都与原数据计算所获得的前端速度点十分接近。

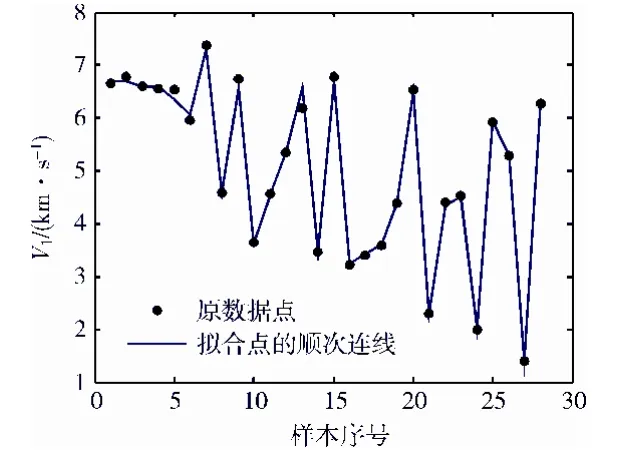
图1 前端速度模型的拟合效果Fig.1 Fitting curves of the maximal axial velocity

2.2 前端速度的预测

为了检验多项式模型的建模精度，将表3中的最后3 个样本作为验证样本代入模型，依次得到碎片云的前端速度的预测结果分别为6.745 2 km/s、7.401 3 km/s、6.520 2 km/s。而与其对应的3 个碎片云的前端速度的试验值分别为6.901 0 km/s、7.608 8 km/s、6.586 5 km/s。结果显示，这3 个预测结果的方均根误差为0.154 6，平均相对误差为1.99%。

3 多项式模型与无量纲化模型的比较

首先考虑无量纲化模型对于表3中的22 个建模样本的拟合问题。当c为任意实数时这是一个不能线性化的非线性最小二乘问题，目前大多采用随机搜索法来解决此类问题。为确定搜索的初始点，将无量纲化模型改写为

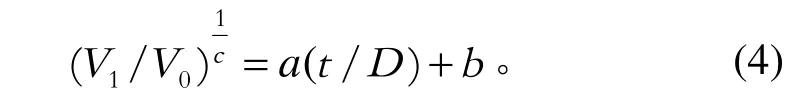
这是一个关于t/D的线性模型，当V1/V0≠0 时而当a=0、b=1 时，等式(4)右端 的值是1，因此1/c应当在0 的附近寻求。

选择a=0，b=1，c=10 作为初始条件，则目标函数为

其中V1i，V0i，ti和Di分别表示V1，V0，t和D的第i个样本。利用文献[11]所给出的二阶段变半径随机搜索算法可以求得=±105，= (m10-5×0.830 9, 1±10-5×0.028 6)。

结果显示，这3 个预测结果的方均根误差为0.227 9，平均相对误差为3.03%。

与多项式模型的预测结果对比可以看出，无量纲化模型无论预测结果的方均根误差还是平均相对误差都要来得大，而且本身不能转化为线性模型，参数的求解十分复杂。

4 结束语

本文提出的预测碎片云前端速度的三元二阶多项式模型属于线性模型，因此其中的参数可以利用最小二乘法求解；但为避免非奇异问题，逆矩阵一律由广义逆矩阵代替。该模型具有更强的泛化能力，可以更好地拟合试验样本，对前端速度具有更好的预测效果。

（References）

[1]Lai S T, Murad E, McNeil W J.Hazards of hypervelocity impacts on spacecraft[J].Spacecraft &Rockets, 2002, 39(1):106-114

[2]Kinslow R.High-velocity impact phenomena[M].New York:Academic Press, 1970:121-145

[3]Piekutowski A J.Formation and description of debris clouds produced by hypervelocity impact, NASA Contractor Report 4707[R], 1996

[4]Kessler J.Collision cascading:The limits of population growth in low Earth orbit[J].Advances in Space Research, 1991, 11(12):63-66

[5]Giacomuzzo C, Francesconi A, Anselmo L, et al.Impact risk analysis for a spacecraft in Cosmo-Skymed orbit[J].Advances in Space Research, 2010, 46(7):846-858

[6]Schäfer F K.An engineering fragmentation model for the impact of spherical projectiles on thin metallic plates[J].International Journal of Impact Engineering, 2006, 33:745-762

[7]Klinkrad H.Space debris:models and risk analysis[M].Chichester:Praxis Publishing Ltd, 2006:5-57

[8]黄洁, 马兆侠.超高速撞击碎片云运动特性及碎片云分布模型研究[C]//第六届全国空间碎片学术交流会论文集.北京:国家国防科技工业局系统工程一司, 2011:358-365

[9]安凯, 马佳光, 傅承毓.超球聚类模糊神经网络在跟踪控制中的应用[J].系统工程与电子技术, 2001, 23(8):80-83 An Kai, Ma Jiaguang, Fu Chengyu.The application of fuzzy neural based on super-sphere clustering in tracking control[J].Systems Engineering and Electronics, 2001, 23(8):80-83

[10]安凯, 邢进生, 邱祖廉.模糊神经网络的二阶段变半径随机搜索算法[J].自动化学报, 2000, 26(5):616-622 An Kai, Xing Jinsheng, Qin Zulian.Two-stage random search algorithm of fuzzy neural network with variable radius[J].Acta Automatica Sinica, 2000, 26(5):616-622

[11]An Kai, Ma Jiaguang, Fu Chengyu.Maximum likelihood estimation of the identification parameters and its correction[J].Systems Engineering and Electronics, 2002, 13(4):31-38