风电功率模拟生成模型研究

张远实，潘延林

（哈尔滨工业大学电气工程学院，黑龙江哈尔滨 150001）

自20世纪90年代以来，全世界风电行业稳步持续发展，风电总装机容量每年以超过15%的速度不断增长着[1]。对风电功率水平作预先规划研究是风电场并网运行的先决条件，而规划研究需要的原始数据主要来自于风电功率的模拟生成。如不预先进行规划研究工作，风电场有效的装机容量将受到很大的制约，较大一部分风能资源会被浪费掉。风力发电功率模拟生成数据的准确性关系到电网的供需平衡，并且直接影响到并网系统运营成本以及电力系统的稳定性和安全性[2-3]。风电功率模拟的统计方法一般不考虑风速突变，主要考虑宏观规律和发展趋势，根据风强的实测数据和实时数值对风电场输出功率进行一个粗略的预先模拟。模拟中需要建立一个数学模型，而模型的正确性是通过往年的数据来分析验证的。风电功率模拟的主要方法有：时间序列法，人工神经网络法，支持向量机法以及灰色预测法等[4]。由于这些算法可以不考虑实际过程，其中涉及到的运算比较简单，主要是用观察分析的方法为风电功率建立一个基于历史参数的模型，这些统计参数来源于往年统计分析的结果。物理方法侧重对风力发电物理过程的研究，并且将物理过程抽象成一个复杂的数学模型。物理方法的主要缺点是计算量较大，用相关软件进行运算时耗时较长[5]。这些方法均不太切合中国风电事业的国情。而我国风电事业发展迅速，在普及风电场的过程中，在一些特殊地域建立风电场时迫切需要进行专门的风电功率模拟。在风电领域领先的一些国家和地区，几乎所有大型的风电场都设计了单独的部门专门负责统计分析历史数据、设置统计参数以及模拟中长期的风电功率。我国不能依赖于套用这些国家建立的模型和装置，需要自主研究适合国情的风电功率模拟生成体系。

因此，本文提出通过随机过程模拟生成风电功率曲线的方法。该方法由于综合考虑到我国风电功率的一些基本特性，因此适合我国风电事业基本情况。

1 风电功率模拟生成模型的建立

1.1 适合模型的随机微分方程的建立

考虑到如式（1）所示的随机微分方程：

式中，Bt是布朗运动；σ是Xt的正函数。

1.1.1 自相关方程

假定式（1）中的σ形式固定，那么可以得到期望E的一个固定解决方法，以及边界条件φ，转化的过程，Yt=E－Xt。

可以得到：

因此：

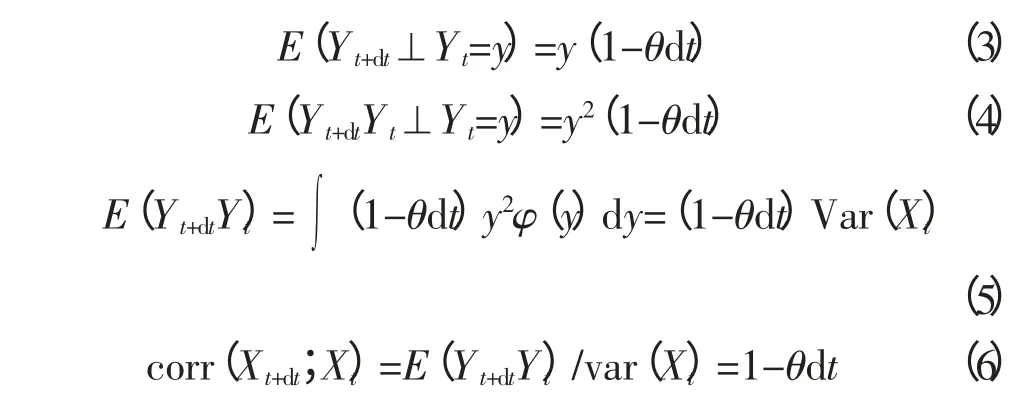
对于任意h＞0，可以将corr（Xt+h；Xt）看作一个结果[5]：

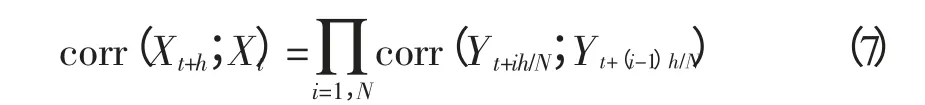
因此，如果扩散系数σ是式（7）的形式，那么Xt和边界法则φ固定，那么Xt的自相关系数是期望的指数衰减形式。

1.1.2 扩散系数的解释

如果Xt是遍历性的，那么限定法则φ和速度测量密度是成比例的，在这里意味着K是定值以及x*是区间（0，γ）上的任意给定值：

对于σ的定义：ρ（x）=φ（x）σ2（x），然后计算log（ρ）的导数：

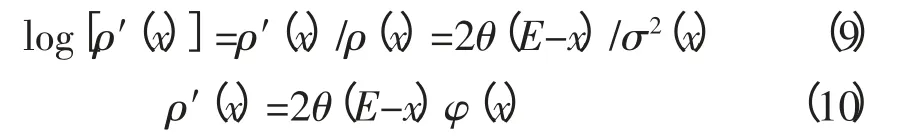
通过整合可以得到对于某个C：

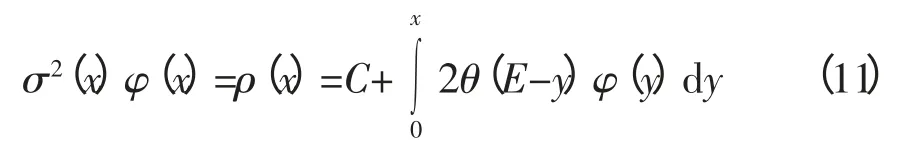
对于遍历性的Xt，一个必要的条件是过程的比例函数在两边边界发散。这意味着x*和y*可以是（0，γ）上的任意给定值。

假定φ（x）是一个Beta分布函数，可以得到以下关于σ（x）的公式：

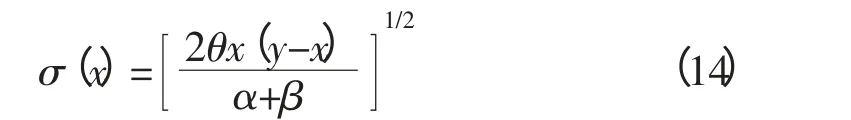
于是，所求的随机微分方程为：

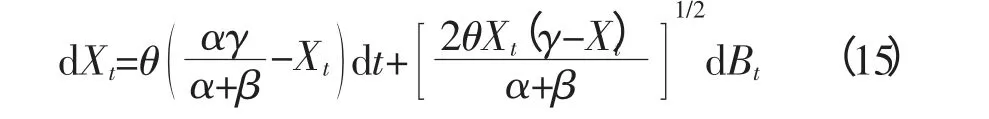
1.2 符号说明

用数学符号来给当前的每月风电功率模拟问题一个具体的表述形式，如表1所示。

为给出问题的解析形式，提出两个假设：

假设1：Xn的自相关函数近似为指数衰减函数。

假设2：φ的形状被近似为参数α、β和γ的Beta分布。

因此，对x∈（0，γ）：

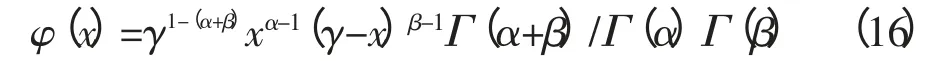
式中，Γ为欧拉函数。

表1 每月风电功率模拟相关符号Tab.1 Related simulation symbols of monthly wind power

φ作为一个Beta分布函数，它由下列方程控制：

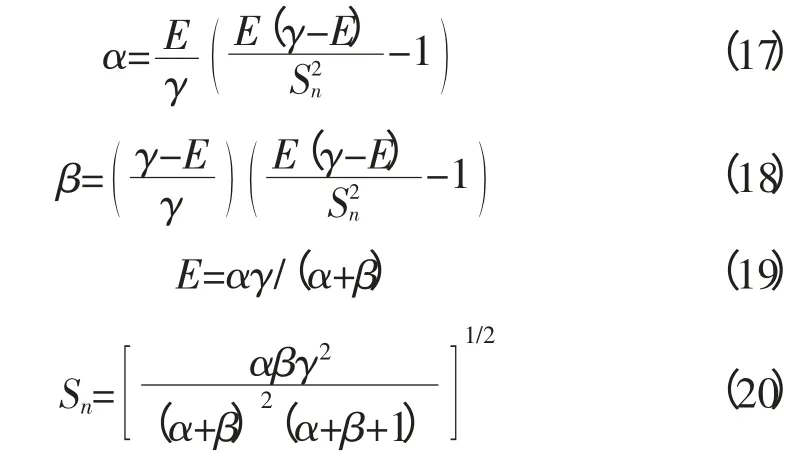
选择Beta分布作为得到Xn概率密度的方法很普遍，因为这种形式的分布适用于3个给定参数E，Sn和γ的任意一系列实验值。

威布尔分布尽管经常适用于风电功率预测问题，在这里却反常地不适用。因为它通用性低得多且不是定义在一个边界区间上。

这个问题现在可以被重新构建为：找到一个定义在区间（0，γ）上关于固定过程X（t）的随机微分方程，它有一个Beta分布边界条件的φ函数且自相关函数是关于θ的指数衰减函数。

1.3 建模的基本约束

要被构建的和实际风电功率系统运转状态相似的时间序列必须符合一些可能性约束。

这些约束应该最少涉及以下内容：

1）这条曲线代表模拟的全年每小时风电功率密度，也就是说在以小时为单位的某一比例的时间期间达到一个给定发电水平，并且一定要与实际风电功率密度相近。

2）一年中，连续月份的发电水平有明显差异，冬天风比夏天强；随机系列应该表现一个相关分布，这意味着和实际发电有相似的期望和变动。

3）功率水平每天中有可察觉的不同。例如，上午3点功率水平每月的平均值与下午6点有很大的不同。随机序列应该相应的表现出来。

4）由于风可能突然变强或变弱，实际风电功率间隔一小时的变化可以达到任意值。

于是，随机的时间序列应该反映一种特殊的随机性和规律性的混合状况，这些也是模拟系统的特征，这一特征强烈暗示研究建立一种基于扩散过程的系统的可能性。

更加具体地说，这个方法是寻找一个随机微分方程；有了合适的随机微分方程，建立随机时间序列将水到渠成，因为只需将其转化为离散形式。

然而，为了使建立的模型符合实际情况，还需要结合条件进行改进：由于季节和一天内变动的限定，实际的物理过程不能直接用单独时间参数的随机微分方程模拟。

在最初的风电功率模型中，应该先不考虑季节性和一天内风电功率变动等问题。

1.4 季节性和一天内变动问题

季节性的问题可以很容易被处理，最简单的方法是把每年的问题分成12个独立月的问题，用独立的随机微分方程表示。

在建立小时的曲线跨越一年时，如果用特定的仿真软件模拟，将改变核心的随机微分方程，因为它从一个月转变到另一个月。

一天内差异问题则用不同方法来处理。最直接的方法是把实际的过程转化为一个标准化的过程，在这个过程中基于一天内风电功率平均水平对每小时的功率水平进行缩减和放大。

在对原始时间序列归一化后，每个修改后的月风电功率模拟过程应该与马尔科夫过程近似相同。

在实际仿真过程中，适合标准化过程的随机微分方程将被用作去产生标准化的随机时间序列，其中一天内功率变动的问题将通过应用一套合适的比例系数补偿。

2 模型求解方法

在第1节中已完成建立数学模型及将模型抽象成为一个随机微分方程的工作。但是此方程由于含有布朗运动这一随机分量，很难直接对此微分方程进行求解。

先将含布朗运动分量从方程中分离出来，对其单独设计算法，得到布朗运动的随机时间序列。再将微分方其带入原方程，简化方程的形式，然后对简化后的离散微分方程进行求解。

2.1 随机微分方程的简述和转化

方程（15）为已建立的随机微分方程，其中Bt是布朗运动α、β、γ和θ为统计得来的4个参数。

根据模型要求，所求微分方程解的形式为以小时为间隔的离散形式。

于是，布朗运动分量dBt可经过形式转化，成为一个随机时变函数random（t）与dt相乘的形式[6]。

方程（15）可以转化为：

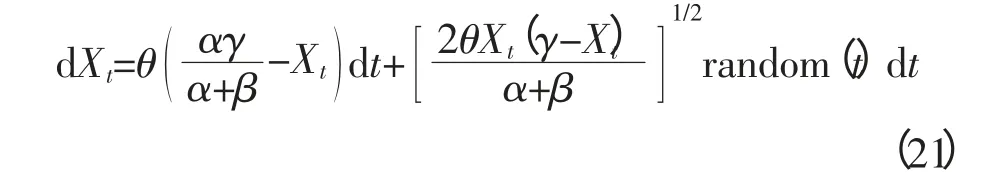
随机时变函数random（t）是对布朗运动的模拟的结果，其形式是一组随机时间序列[6]。

于是，方程（21）可以看作一个带随机时变系数random（t）的常微分方程。

2.2 布朗运动的模拟

一维布朗运动模拟的流程图如图1所示。为了保证转化的合理性，模拟布朗运动程序仿真的步长应结合实际情况选定，最大步数由区间初始值和步长确定。只要保证最大步数大于当前月的总小时数即可，而不必严格与其相等。由于风电功率模拟生成的结果是以总装机容量的百分数表示的，没有实际单位，于是应对布朗运动的结果进行归一化处理。

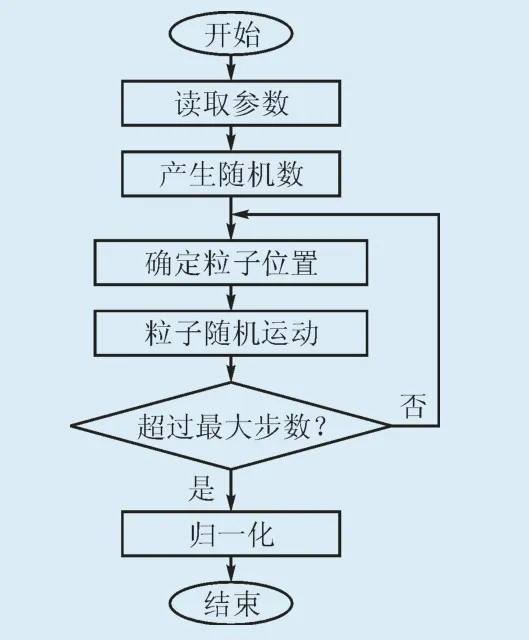
图1 一维布朗运动模拟流程图Fig. 1 Flow chats of one-dimensional Brownian motion

2.3 月风电功率的模拟生成

根据已建立的模型，考虑到季节性差异的问题，将年过程划分成12个的独立月过程，用12个不同的随机微分方程进行求解[8]。

模拟生成月风电功率的流程图如图2所示，主要步骤为：

图2 月风电功率生成流程图Fig. 2 Flow chart of monthly wind power simulation

1）首先将月风电功率原始数据保存在文档或表格中，并用Matlab读取数据。然后将数据结合模型要求做简单的处理，生成所需的统计参数。

2）运行布朗运动的模拟程序，得到布朗运动随机时间序列。该序列用于作为随机微分方程的时变系数。

3）模拟的月风电功率过程以小时为单位，随机微分方程需要每小时初值。利用合适的随机数学分布产生每小时功率初始值

4）在1）—3）各步的基础上，利用Matlab中的ode45函数解转化后的随机微分方程，并得到小时功率时间序列。判断是否超过月时间总长度，如未超过循环执行以上步骤，反之跳出循环。

5）生成月功率时间序列，利用Matlab作出每月概率密度分布图。

6）每月模拟过程步骤相同，但核心的随机微分方程参数不同，需要修改相关参数及月时间总长度。

模型中已提到，风电具有随机性、间歇性以及不可控性，实际风电功率间隔一小时的变化可以达到任意值，故每小时功率水平的初始值应是一个在由统计规律生成的区间中的随机数，可以假设其服从均匀分布或正态分布[9]。不能采用前一小时的模拟值作为后一小时的初始值。

式（21）所述将布朗运动形式转化的目的在于，由于软件求微分方程的数值解需要选定步长，如果布朗运动的步长与其一致，随机微分方程可转化为带时变系数的常微分方程来进行求解。这样将复杂的随机微分方程求解过程大大简化，同时也提高了模拟过程的精度，大大减小了误差[10]。

基于微分方程（21）的形式，Matlab中可选用的函数有解显式微分方程的ode45和隐式的ode15i[11]。

下面简单介绍一下这两种函数。ode45函数主要适用于非刚性问题的求解，其特点为一步法、采用4阶的龙格库塔（Runge-Kutta）方程、其累计阶段误差为Δx的5阶无穷小；而ode15i适用于解刚性问题，为多步法、采用Gear’s反向数值微分、精度中等，ode15i函数经常在当应用ode45函数失败时使用[12]。

3 算例分析

为得到较全面的结果，本文选取了中国和西班牙两个算例。主要对月功率水平的平均值和标准偏差，年功率水平的标准偏差，以及月概率密度分布图和年概率密度分布图进行了程序模拟。

西班牙算例的原始数据为西班牙2002年全年80%以上风电场的统计数据，中国算例则是大丰风电站、东台风电站、国华风电站、响水风电站4个大型风电站的详细运行数据。

两国的算例原始数据均存在小部分的缺失，其中西班牙较为严重，可能对仿真结果造成一些小的影响。

3.1 算例1——西班牙

据统计，西班牙2002年全年每小时功率水平的平均值为25.5%，标准差为14.1%（用总装机容量的百分数表示）。

根据模拟结果，西班牙2002年全年每小时功率水平的平均值为25.25%，标准差为15.46%（用总装机容量的百分数表示）。与统计数值25.5%的平均值、14.1%的标准差比较，发现平均值极为接近；而标准差虽然略微高估，但是和每月数据相比，其误差已经缩小很多。由此可见，样本容量越大，数据越充足，所用模拟方法与实际越接近。

此外，从模拟结果得到每月超出允许范围（小于零或者超过γ或超过1）的数据除一月所占比例为4.04%外，其他月份均接近于0，可见模拟方法较为合理，一月数据怀疑是统计参数缺乏有效实际时间序列造成的。

将各月风电功率时间序列合并成年风电功率时间序列，可得到西班牙年风电功率概率密度分布图，如图3所示。

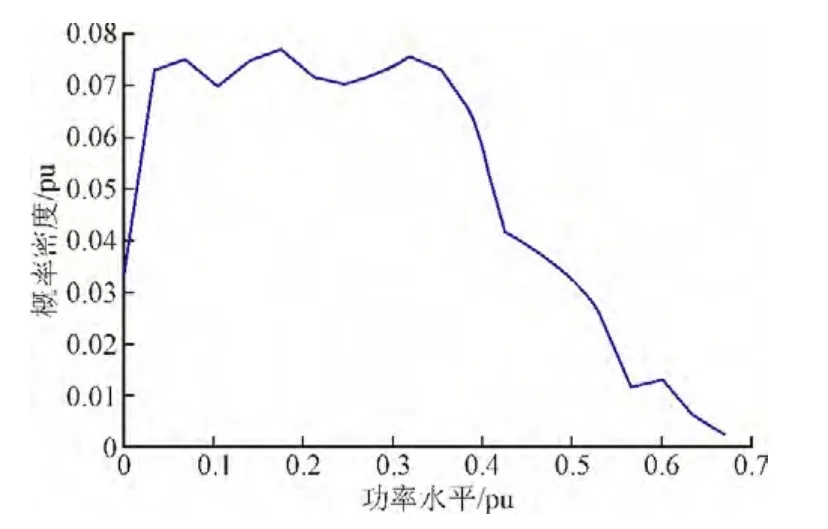
图3 西班牙年风电功率概率密度分布图Fig. 3 Wind power probability density distribution chart of Spain

由图3可见，年概率密度分布图更加趋于平滑，在每个功率范围其概率的分布较为均匀，在功率较小的范围概率较大，在功率较大的范围概率较小，与实际情况相符。

3.2 算例2——中国

本例中所有风电功率水平的值均表示为4个风电场同一时刻的实际功率之和占总装机容量的百分数。

根据模拟结果，中国2011年4个风电场全年每小时功率水平的平均值为14.49%，标准差为14.73%（用总装机容量的百分数表示）。与统计数值14.26%的平均值、15.12%的标准差比较，发现平均值较为接近；而标准差虽然略微高估，这与各月的综合情况基本相符。在这一点上中国算例与西班牙算例基本一致。此外，从全年模拟结果来看超出允许范围（小于0或者超过γ或超过1）的数据占5.02%，这一项比西班牙算例大得多。

将各月风电功率时间序列合并成年风电功率时间序列，可得到中国年风电功率概率密度分布图，其中红色虚线为模拟的风电功率概率密度曲线，蓝色实线为实际的风电功率概率密度分布图，如图4所示。

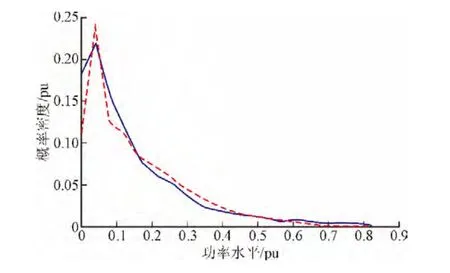
图4 中国风电功率概率密度分布图Fig. 4 Wind power probability density distribution chart in China

从图4可以看出，实际和模拟曲线非常接近，整体趋势基本一致。 利用本文提出的风电功率模拟生成模型及其求解方法可以用于全年风电功率序列的模拟，模拟结果可以很好地体现规划研究中所需的一些统计规律。

4 结论

本文主要针对大规模风电功率时间序列的算法进行研究，重点在于研究形式为随机微分方程的数学模型的算法，提出了解决离散随机微分方程的一种简单算法，利用随机过程产生风电功率时间序列，建立了风电功率模拟生成模型，从中抽象出了形式为随机微分方程的数学模型，并且提出了一种解决方法。算例结果验证了模型的可行性和解法的有效性。

[1] 张谦，李琥，高松. 风电对调峰的影响及其合理利用模式研究[J]. 南方电网技术，2010（6）: 18-22.ZHANG Qian，LI Hu，GAO Song. Research on the impact of wind power on peak load regulation and its rational utilization mode[J]. Southern Power System Technology，2010（6）: 18-22（in Chinese）.

[2] 余洋，陈盈今，刘立卿，等. 大规模风电接入对电网电压稳定性影响的研究[J]. 电力科学与工程，2010（4）:1-4.YU Yang，CHEN Yingjin，LIU Liqing，et al. Study on effect of voltage stability about large scale interconnected wind farm[J]. Electric Power Science and Engineering，2010（4）: 1-4（in Chinese）.

[3] 任新伟，徐建政，赵斌. 含光伏电站的配电网无功优化[J]. 电力电容器与无功补偿，2014，35（1）: 11-15.REN Xinwei，XU Jianzheng，ZHAO Bin. Reactive power optimization of distribution network containing PV power station[J]. Power Capacitor ＆ Reactive Power Compensation，2014，35（1）: 11-15（in Chinese）.

[4] 张旭，牛玉广，马一凡，等. 基于功率谱密度的风电功率特性分析[J]. 电网与清洁能源，2014，30（2）: 93-97.ZHANG Xu，NIU Yuguang，MA Yifan，et al. Wind power characteristic analysis base on the power spectral density[J].Power System and Clean Energy，2014，30（2）: 93-97（in Chinese）.

[5] 袁越，李强，李群，等. 风电功率特性分析及其不确定性解决方案[J]. 电力科学与技术学报，2011，26（1）: 67-72.YUAN Yue，LI Qun，LI Qun，et al. Wind powet characteristics analysis and it suncertainey solution[J]. Journal of Electric Power Science and Technology，2011，26（1）: 67-72（in Chinese）.

[6] 沈焰焰，施齐焉. 随机微分方程的的Runge-Kutta数值解法[J]. 福州大学学报：自然科学版，2009（37）: 317-321.SHEN Yanyan，SHI Qiyan. Runge-Kutta methods fomumerical solutions of stochastic ordinary differential equations[J]. Journal of Fuzhou University：Natural Science Edition，2009（37）: 317-321（in Chinese）.

[7] 胡建成，罗敏. 随机常微分方程的龙格库塔解法[J]. 四川大学学报：自然科学版，2012，49（4）: 747-752.HU Jiancheng，LUO Min. Stochastic Runge-Kutta solution of ordinary differential equations[J]. Journal of Sichuan University：Natural Science Edition，2012，49（4）: 747-752（in Chinese）.

[8] 王松岩，于继来，李海峰，等. 考虑统计和互相关特性的多风电场风速数据模拟生成方法[J]. 电力系统自动化，2012（36）: 1-7.WANG Songyan，YU Jilai，LI Haifeng，et al. A wind speed modeling method for multiple wind farms considering correlation and statistical characteristics[J]. Automation of Electrical Power System，2012（36）: 1-7（in Chinese）.

[9] 周伟. 随机微分方程数值解[D]. 武汉：华中理工大学，1997.

[10] LOJOWSKAA，KURO WICKAD，PAPAEF THYMONG，et al. Advantages of ARMA_GARCH wind speed time series modeling[C]// Proceedings of IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems，June 14-17，2010. Singapore: 83-88.

[11] PHILIPPOPOULOSK，DELIGIORGID. Statistical simulation of wind speed in Athens，Greece based on weibull and ARMA models[J]. International Journal of Energy and Environment，2009，3（4）: 151-158.

[12] NIELSEN T S MADSEN，H. WPPT：a tool for wind power prediction[C]// EWEA Special Topic Conference，Kassel，2000.