含风电场的电网储能系统选址和优化配置

刘小寨，徐天，葛立坤，张雪莉

（1. 国网乌鲁木齐供电公司，新疆 乌鲁木齐 830000；2. 华北电力大学，北京 102206）

现阶段我国风光储示范项目正在逐步开展，如国家电网的张北风光储输示范项目与南方电网的储能示范项目。张北项目是世界首个风光储输示范项目，实现了平滑风光功率输出、跟踪风光计划发电、辅助削峰填谷、参与系统调频四种功能[1]。该项目一期工程为100 MW的风电和40 MW的光伏发电，并配置了20 MW的储能，其中14 MW的锂离子电池储能系统已经投运，从目前的运行情况看，储能技术能满足风电和光伏发电并网的功能性要求，并起着重要的作用[2]。

关于储能系统选址和容量配置以及对风电并网接纳能力方面，风电并网接纳能力的量化研究通常采用比较粗略的指标，很难有通用的准则，而在此基础上配合接入的储能系统的选址和容量配置工作也大多从经济性角度出发，或由预测的累积误差来确定，很少有从储能系统对大规模风电并网运行性能的影响和改善方面出发来进行选址[3-6]。文献[7]根据不同风电场和储能系统的容量配比关系提出了一种配置大规模储能系统的方案，初步优化了储能系统的容量。文献[8]提出了基于机会约束规划的混合储能容量配置方法。文献[9]为配电网中的储能系统的应用提出了一种长期优化和短期优化相结合的阶段方案。文献[10]针对风电场中的集中储能和分布式储能的特性分别分析了储能安装容量的最优范围。但以上研究多是对储能系统容量的分析，缺少对选址以及在选址的基础上进行容量优化的研究[11-12]。本文为了实现储能系统的选址和容量的优化配置，从安全、稳定、经济性3个方面选取评估指标，指导储能系统进行选址和容量的初步配置，并利用多目标最优潮流计算得到最优解下的储能系统有功、无功出力，实现储能系统容量的优化。

1 储能系统选址评估

1.1 评估指标的选取

1.1.1 安全性评估指标

针对含大规模风电的电网，电压安全首先需要满足评判标准。为了准确地量化电网电压的稳定性水平，本论文给出一个新的定义，即电网电压越限距离D。电网电压越限距离D定义为电网当前运行点电压与正常运行时电压目标值之间的“距离”，值越小越好，计算方法见式（1）。

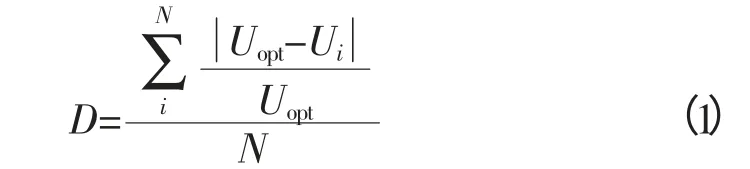
式中，Uopt为正常运行时电压目标值；Ui为当前运行点的节点电压；N为待考察的电网评估点数量。

1.1.2 稳定性评估指标

利用特征值分析方法对系统小干扰稳定性进行研究，所关心的只是状态矩阵中与分析目的密切相关的特征值部分。所以，本文选取系统矩阵临界特征值的实部Zreal作为稳定性评估指标。只有特征值在复平面的左半部分时，系统才是小干扰稳定的[13-14]。

1.1.3 经济性评估指标

为了使电力系统在功率均达到平衡的前提下，尽可能地使全网有功功率损耗ΔP最小，本文选取网损贡献度Closs为经济性评估指标[15]。Closs表示在储能系统接入后引起整个电网网损的变化程度，计算方法见式（2）。

式中，ΔP+、ΔP-为储能系统接入前/后全网的有功损耗；Closs即引起的全网的网损减小量与并网前全网网损量之比，值越大表示储能接入后全网网损减小的越多。

1.2 评估指标模型的建立

由于各指标之间量纲不同，需要对指标进行归一化处理。由3个带权衡系数的目标子函数加权得到最终的目标函数。见式（3）。

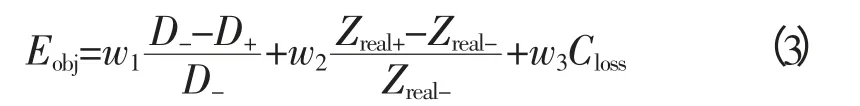
式中，wi（i=1，2，3）为权重系数且w1+w2+w3=1。3个权重系数的取值大小表明该指标在整体评估中所占的比例；不同数值的3个权重系数组合对应着不同的评估方案，且Eobj越大越利于系统的稳定。

2 基于多目标最优潮流的储能系统容量优化配置

本文基于电力系统最优潮流（Optimal Power Flow，OPF）算法，建立多目标最优潮流模型，实现储能系统成本最低的同时，也实现无功补偿费用最低、有功损耗最小以及提高风电接纳能力的多重目标；这样的配置结果不仅可以使储能系统运行最经济，而且可以最大限度发挥储能系统的作用，实现电网的经济稳定运行。

首先，模型建立的前提条件如下：

1）各发电厂投入运行的机组已知，不解决机组开停问题；

2）各发电机组的输出功率已定且由发电厂经济调度确定；

3）电力网络结构确定，不受接线方式影响，不考虑网络重构问题。

2.1 多目标最优潮流的目标函数

本论文模型中所涉及的变量划分为控制变量及状态变量。控制变量包括Pc、Qc和Qgi；状态变量通常包括Ui、Pi和Pj等。

1）目标函数一：储能系统有功费用最低

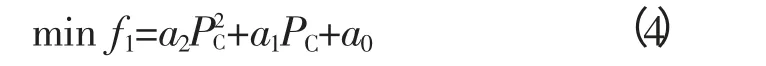
2）目标函数二：储能系统无功费用最低

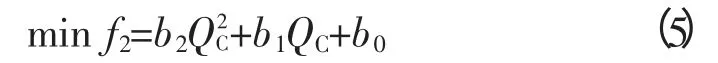
式中，Pc和Qc分别为储能系统的有功、无功出力；a2、a1、a0、b2、b1、b0分别为储能系统有功、无功成本耗量特性系数。

3）目标函数三：无功补偿费用最低

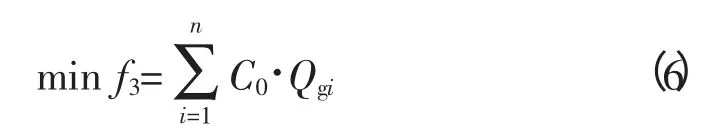
式中，C0（元/kvar）为考虑了装设无功补偿设备修正后的单位无功容量价格。Qgi（kvar）为第i个负荷点的无功补偿容量，Qgi>0表示装设电容器或调相机，Qgi<0表示装设并联电抗器。

4）目标函数四：有功网损最小

式中，PGi和PDi分别为支路注入的有功功率和流出的有功功率，它们的差值为支路上的有功损耗；n为支路条数。

5）目标函数五：电压偏差最小

式中，Ui为节点电压幅值；U軍为电压的目标值，它们的差值为节点电压偏差；n为节点个数。

最终，利用权重因子αi形成多目标最优潮流模型，其目标函数为：

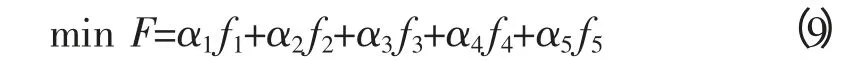
2.2 多目标最优潮流的约束条件

2.2.1 等式约束条件

等式约束为各节点注入有功功率和无功功率平衡约束，即潮流约束：

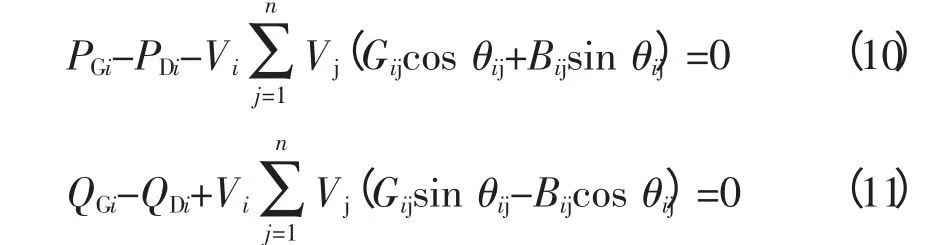
2.2.2 不等式约束条件

不等式约束表示的是电力系统安全运行和电能质量约束，包括：

1）节点电压约束

2）支路有功潮流约束

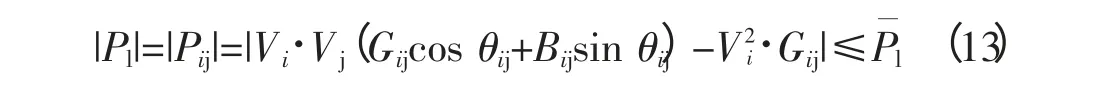
3）储能系统有功和无功出力约束

4）可调有功电源出力约束

3 算例分析

本文在PSASP仿真平台上搭建了8机36节点系统模型，该系统包含8处发电厂和8座220 kV带负荷枢纽变电站，如图1所示。由于目前DFIG已成为大中型风电场的主流机组，因此本文将风电场等值为1台风电机组，在PSASP仿真平台上搭建“双馈风力发电机组”模型，视为PQ节点，其中Q=0，cosΦ=1。另外，在PSASP仿真平台上搭建“通用储能系统”模型，该模型将储能系统作为节点功率注入，视为PQ节点，端口电压跟随电网电压。

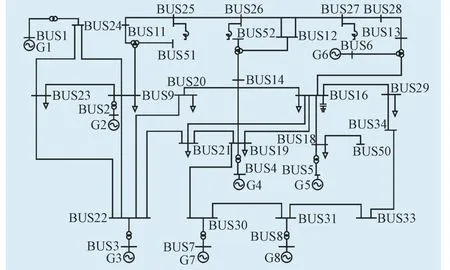
图1 仿真接线图Fig. 1 The simulation wiring diagram

本文中的储能系统配置方式采用MESS（mass energy storage system）集总式，含大型风电场和MESS的电网模型如图2所示。

图2 含风电场和储能系统的电网模型Fig. 2 The grid model with wind farms and energy storage system

MESS的接入电压等级应为220 kV及以上，因此本文中的储能系统模型先接入变电站380 V母线，然后通过升压变压器与10 kV母线连接，最后接入220 kV枢纽变电站。

3.1 储能系统的选址评估

参数采用标幺制计算，功率基值为100 MV·A，基准电压为额定电压。总发电为26.573+j14.762，总负荷为25.688+j10.448，假定负荷是不变的。

3.1.1 评估指标的计算与分析

将储能系统依次接入电网中8个220 kV负荷母线节点，逐渐增加储能系统的有功、无功大小，D+、Zreal+、Closs+这3个指标的变化趋势分别如图3、图4和图5所示。

图3 安全性评估指标D+Fig. 3 Safety evaluation index D+

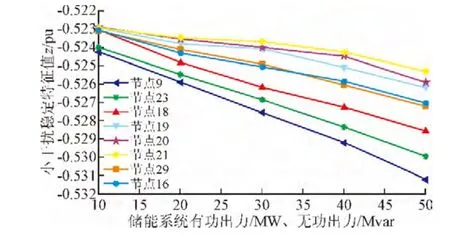
图4 稳定性评估指标Zreal+Fig. 4 Stability evaluation index Zreal+

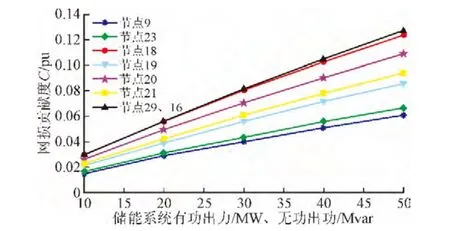
图5 经济性评估指标Closs+Fig. 5 Economic evaluation index Closs+

由以上结果可以看出，一方面，在储能系统总出力相同的情况下，不同点接入所达到的效果也不同。以安全性评估为例，节点18的电网电压越限距离指标明显小于其他节点，表明该点接入储能系统后电网整体电压水平最高。另一方面，在不改变储能系统接入位置的情况下，电压支撑由储能系统的总出力决定，与负荷的比值越高，电压支撑就越大，整体电压水平就越高，网损也越小。

3.1.2 储能系统选址评估结果

本文根据不同的权重系数wi的组合确定了3个不同的评估方案，如表1所示。

表1 评估方案Tab. 1 Evaluation schemes

方案一中，经济性评估指标的权重为0，该方案只考察不同接入位置下储能系统对电网电压运行水平和电网稳定性的影响程度，不关心电网运行的经济性；方案二中，安全性评估指标的权重最高，经济性评估指标的权重最低，该方案侧重于考察不同接入位置下储能系统对电网电压运行水平的影响程度；方案三中，经济性评估指标的权重最高，该方案侧重于考察不同接入位置下储能系统对电网运行经济性的影响程度。最终，3个方案的评估结果如图6、7、8所示。

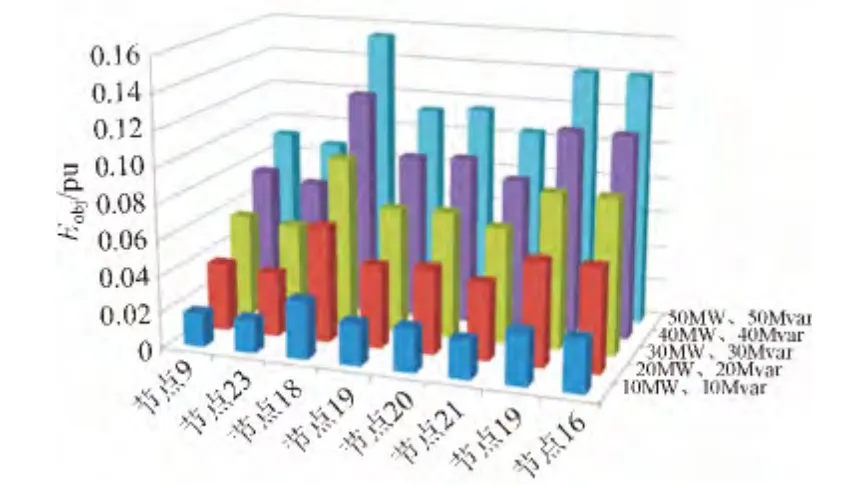
图6 方案一评估结果Fig. 6 The program 1 results

图7 方案二评估结果Fig. 7 The program 2 results

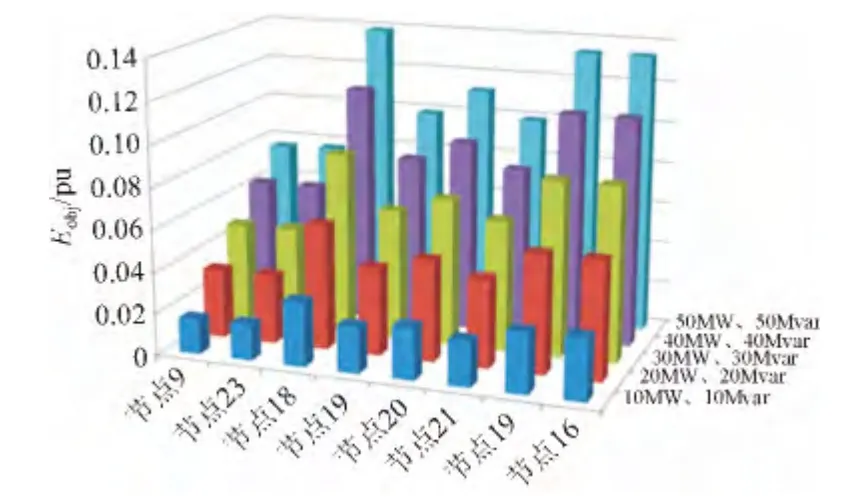
图8 方案三评估结果Fig. 8 The program 3 results

评估结果分析如下：

1）3个方案的评估结果均得到节点18的目标函数值最大，所以节点18为储能系统最为合适的接入点。其中，这3个方案权重偏高则表明该方案侧重于该项指标的评估。

2）在含大规模风电场的发输电网中，配备储能系统可以改善系统潮流分布，大幅提高电网接纳风力发电的能力。

3.1.3 储能系统容量初步配置

在储能系统接入前，节点9的风电最大注入功率为128 MW；节点18接入储能系统后逐渐增大其有功、无功出力，最终可满足节点9接受150 MW的风功率。此时，储能系统出力大小与节点9可接受的最大风功率之间的配比关系如图9所示。

由图9可看出，一方面随着储能系统出力增加，电网可接受的风电场规模也增大；另一方面，储能系统出力的增加与并网风电场规模增大之间的关系并不是线性的，因为考虑到风电场的广域平滑特性可以降低风电场输出总功率的波动，因此储能系统出力和风电场最大注入功率的比值随着风电场规模的增加呈现下降趋势。

因此，满足节点9最大风功率为150 MW的储能系统有功、无功最大出力的配置方案有无穷种。从中选取5种具体的配置方案，如图10所示，即为在选址基础上实现的储能系统容量初步配置。

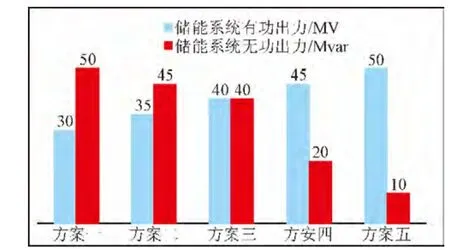
图10 满足风电接纳能力的储能系统容量初步配置Fig. 10 The storage system capacity preliminary schememeeting wind power receptiveness

3.2 储能系统的容量优化配置

3.2.1 容量初步配置下的潮流数据

首先，系统初始状态下，PQ节点电压上下限值分别设置为0.95和1.05；支路有功潮流限值为1；储能系统有功出力上限值为50 MW，无功出力上限值为50 Mvar；无功补偿容量上限值为30 Mvar。

然后，在储能系统选址的基础上，以及进行容量的初步配置后，选取一种具体配置方案（即图10中的方案三）：储能系统有功出力为40 MW，无功出力为40 Mvar，系统无功补偿功率为26.32 Mvar，此时电网支路有功潮流和节点电压幅值分别如表2和表3所示。

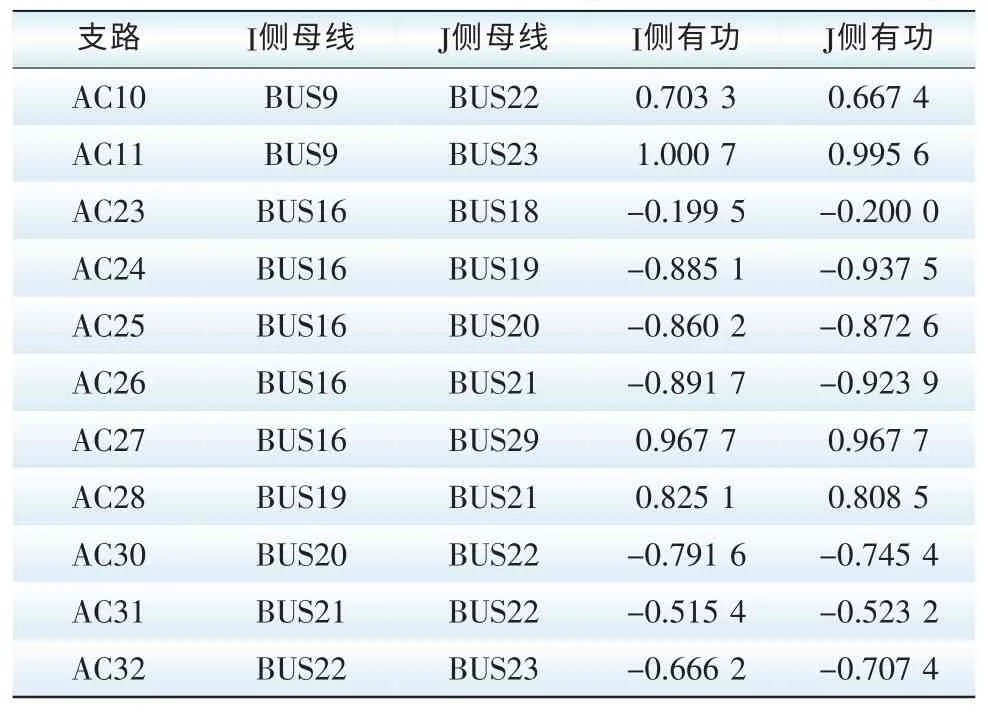
表2 支路有功潮流Tab. 2 Branch active power flow pu

此时，储能系统虽然满足了系统可接纳的风电场最大注入功率，但存在支路潮流越限（AC11的I侧有功大于1）的情况，并且一些节点（如节点22和节点24）的电压接近电压限制，如此长时间运行不利于电力系统的安全稳定。

3.2.2 多目标等权重赋值优化结果

先为OPF模型的目标函数中5个分目标所占总目标的权衡系数进行等系数赋值（αi=0.2），再经过多目标最优潮流计算后，优化后的储能系统的有功出力为33.83 MW、无功出力为36.15 Mvar，无功补偿功率为18.32 Mvar。各目标优化前后结果如图11所示，优化后储能系统的有功、无功出力明显减少，无功补偿功率也有所下降。

表3 节点电压幅值Tab. 3 Node voltage magnitude pu

图11 初始状态与OPF下各目标函数值Fig. 11 The objective function value under the initial state and the OPF

可看出，优化后储能系统有功、无功费用和无功补偿费用明显降低，有功损耗和电压偏差均有所减小。此时，电网节点电压幅值和支路有功潮流分别如表4和表5所示。

表4 节点电压幅值Tab. 4 Node voltage magnitude pu

可看出，在最优潮流分布下支路有功潮流和节点电压均满足限值要求，并且此时电网的潮流分布更加合理，电压水平也有所提高，保证了电网安全稳定运行。

表5 支路有功潮流Tab. 5 Branch active power flow pu

最终，通过优化前后对比可说明，最优潮流指导下储能系统的容量减小，实现了容量优化配置的目标；在降低储能系统出力成本的同时也降低了电网无功补偿的需求和费用以及网络损耗，优化了电网运行的经济性；并且在此基础上，电网的电压偏差减小，整体电压水平提高，功率分布也更加合理，电网运行的安全性和稳定性也得到了优化。

4 结论

本文通过建立电网、大规模风电场和大容量储能系统的模型，并建立评估指标模型，确定目标函数，比较储能系统在各接入点的目标函数值，得到储能系统合理的选址结果和容量的初步配置；利用已建立的多目标最优潮流模型，最终计算得到各优化目标等权衡系数下的目标优化结果及储能系统的总出力，指导了储能系统容量的优化配置。仿真结果表明，储能系统的优化配置，可以大幅度提高风电场的接纳能力、电网的稳定性和经济性。该储能系统选址评估模型和容量优化配置模型将储能问题进行量化，也可为其他类型系统的研究提供一定的参考。

[1] 蒋平，熊华川. 混合储能系统平抑风力发电输出功率波动控制方法设计[J]. 电力系统自动化，2013，37（1）：122-127.JIANG Ping，XIONG Huachuan. A control scheme design for smoothing wind power fluctuation with hybrid energy storage system[J]. Automation of Electric Power Systems，2013，37（1）：122-127（in Chinese）.

[2] 高明杰，惠东，高宗和，等. 国家风光储输示范工程介绍及其典型运行模式分析[J]. 电力系统自动化，2013，37（1）：59-64.GAO Mingjie，HUI Dong，GAO Zonghe，et al. Presetation of national wind/photovoltaic/energy storage and transmission demonstration project and analysis of typical operation modes[J]. Automation of Electric Power Systems，2013，37（1）：59-64（in Chinese）.

[3] 李生虎，丁明，汪兴强. 电力系统静态电压安全问题的概率评价[J]. 电力系统自动化，2003，27（20）：26-30.LI Shenghu，DING Ming，WANG Xingqiang. Probabilistic evaluation to static voltage security of power systems[J].Automation of Electric Power Systems，2003，27（20）：26-30（in Chinese）.

[4] 张雪莉，刘其辉，马会萌，等. 光伏电站输出功率影响因素分析[J]. 电网与清洁能源，2012，28（5）: 75-81.ZHANG Xueli，LIU Qihui，MA Huimeng，et al. Analysis of influencing factors of output power of photovoltaic power plant[J]. Power System and Clean Energy，2012，28（5）:75-81（in Chinese）.

[5] 张坤，毛承雄，谢俊文，等. 风电场复合储能系统容量配置的优化设计[J]. 中国电机工程学报，2012，32（25）：79-87.ZHANG Kun，MAO Chengxiong，XIE Junwen，et al. Optimal design of hybrid energy storage system capacity for wind farms[J]. Proceedings of the CSEE，2012，32（25）：79-87（in Chinese）.

[6] 杨珺，张建成，桂勋. 并网风光发电中混合储能系统容量优化配置[J]. 电网技术，2013，37（5）：1209-1216.YANG Jun，ZHANG Jiancheng，GUI Xun. Capacity optimization of hybrid energy storage system in grid-connected wind and PV power generation system[J]. Power System Technology，2013，37（5）：1209-1216（in Chinese）.

[7] 梁亮，李建林，惠东. 大型风电场用储能装置容量的优化配置[J]. 高电压技术，2011，37（4）: 930-936.LIANG Liang， LI Jianlin， HUI Dong. Optimization configuration for capacity of energy storage system in large-scale wind farm[J]. High Voltage Engineering，2011，37（4）: 930-936（in Chinese）.

[8] 谢石骁，杨莉，李丽娜. 基于机会约束规划的混合储能优化配置方法[J]. 电网技术，2012，36（5）: 79-84.XIE Shixiao，YANG Li，LI Lina. A chance constrained programming based optimal configuration method of hybrid energy storage system[J]. Power System Technology，2012，36（5）: 79-84（in Chinese）.

[9] WESTERMANN D，NICOLAI S，BRETSCHNEIDER P.Energy management for distribution networks with storage systems-A hierarchical approach[C]// Power and Energy Soeiety General Meeting Conversion and Delivery of Electrical Energy in the 21st Century，Pittsburgh，PA，2008:1-6.

[10] LI Wei，GEZA JOOS.Comparison of energy storage system technologies and configurations in a wind farm[C]// Power Electronics Specialists Conference，Orlando，FL，2007:1280-1285.

[11] XUE Yusheng，XU Taishan，LIU Bing，et al. Quantitative assessments for transient voltage security[J]. IEEE Trans on Power Delivery，2000，15（3）: 4-8.

[12] GAN D. THOMAS R J，ZIMMERMAN R D. Stabilityconstrained optimal power flow[J]. IEEE Trans on Power Systems，2000，15（2）: 535-540.

[13] 吴俊玲，周双喜，孙建锋，等. 并网风力发电场的最大注入功率分析[J]. 电网技术，2004，28（20）: 28-32.WU Junling，ZHOU Shuangxi，SUN Jianfeng，et al.Analysis on maximum power injection of wind farm connected to power system[J]. Power System Technology，2004，28（20）: 28-32（in Chinese）.