转化思想在高中数学解题中的应用??
李连明
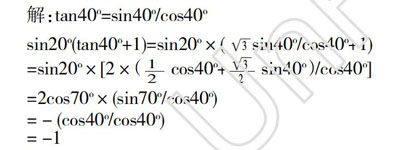

[内容摘要]对很多学生而言,数学这门学科学起来很难,因为数学题永远做不完,而且还以千变万化的形式出现,难以把握所有数学题的解题思路。其实,只要学生掌握了一定的方法,再难的数学题也能迎刃而解。这就要求学生在解题过程中具有转化思想。本文中以具体的数学题为例对转化思想在高中数学解题中的应用进行了阐释。
[关键词]转化思想;高中数学解题;应用
转化思想,也被称为化归思想,是转化与归结的总称。它是一种把待解决或未解决的问题,通过某种转化过程归结到一类已经能解决或比较容易解决的问题中去,最终求得问题解答的数学思想。转化是高中数学解题的一种重要的思想方法,运用非常广泛,转化得当,可以大大减化解题过程,降低解题难度。
一、转化思想在三角函数问题中的应用
三角函数是高中数学教学中的一个难点内容。我们在求三角函数中特殊角的正弦、余弦、正切、余切值时会很容易得到答案,如 30o角、45o 角、 60o角、 90o角,但更多的时候三角函数中出现的角不是这些特殊角,需要查表求值,这就给解题带来了很多麻烦。如果我们能运用转化的思想将不同的三角函数问题转化为同一个三角函数问题,那么解题就会变得很容易。
例如,利用三角公式化简sin20o( tan40o+1),这道题中的20o和40o都不是特殊角,因此要想顺利解出此题,就需要我们对其进行转化。可以通过三角函数中正弦、余弦、正切之间的转化来将问题简单化。
解:tan40o=sin40o/cos40o
sin20o(tan40o+1)=sin20o×( sin40o/cos40o+1)
=sin20o×[2×( cos40o+ sin40o)/cos40o]
=2cos70o×(sin70o/cos40o)
= - (cos40o/cos40o)
= -1
从上述解题过程我们可以看出,此类解题方法充分体现出了转化思想在三角函数问题中的普遍应用。其实,在解决三角函数的化简和求值等实际问题时转化思想随处可见,如 cos-sin2a=cos2a。
二、转化思想在集合问题中的应用
集合是高中数学知识中的一个难点内容,解决某些集合问题时,学生往往不知如何入手,这时需要利用转化思想,将其转化为自己学过的、比较熟悉的知识,以便很快得到答案。
例题: 已知 M=(a,b)|a2+b2=1,N=(a,b)|a+b=1,求 M∩N。
分析:M是N的子集可以转化为 M∩N=M,M∪N=N 。由M、N两个集合中元素的表示形式可知两集合表示的是平面上的点。 M=(a,b)|a2+b2=1,表示以原点为圆心, 1为半径的圆上所有点的集合; N=(a,b)|a+b=1,表示直线a+b-1=0上所有点的集合。所以M∩N表示圆与直线两个图像中的交点。
解:因为M=(a,b)|a2+b2=1,N=(a,b)|a+b=1
所以两图像的交点为 (1,0)、(0,1)。
所以 M∩N的集合为(1,0)、(0,1)。
从此题的解法可以看出,求点的交集问题通常可以转化为求曲线之间的公共点问题,并进一步转化为求方程组的解的问题。也可以将问题用图形表示出来,这样会使问题更形象化,更容易解决。
三、转化思想在概率问题中的应用
高中阶段,我们解决概率问题时,由于概率往往存在对立的情况,如果直接求概率比较麻烦,可以考虑运用转化思想,将问题转化到对立问题上去,先求对立问题的概率,再用1减去对立问题的概率即可。
例题:现在有两个袋子,里面分别有5个小球,两个袋子里的小球上分别标有数字3、4、5、6、7,我们要从两个袋子里分别拿出一个球,将两个球上的数字相加,求两个小球的数字相加的和不等于9的概率。
分析:要想直接求两个小球数字相加之和不等于9的概率,先要分别求出两个小球数字相加之和等于7、8、10、11、12、13的概率,然后将求出的概率相加,这样的解题过程很麻烦。我们可以考虑将问题转换一下:两个小球的数字相加之和不等于9的概率等于1减去两个小球数字相加之和等于9的概率,这样求解就比较容易了。
解:两个小球数字相加之和等于9的情况有四种:3+6,4+5,5+4,6+3,而且所有情况都出现的情形有25种,所以两个小球数字相加之和等于9的概率为 ,因而两个小球的数字相加之和不等于9的概率就为1- = 。
转化思想在高中数学解题中的应用很灵活,它可以将抽象化为具体,将深奥难懂转化为浅显易懂,将复杂化为简单,将生疏化为熟悉,为学生解决数学难题提供一条便捷的路径。熟练应用转化思想,灵活地解决有关数学问题,将有利于提高学生的数学解题能力和技巧。
参考文献:
[1]谢秋影.转化思想在初中数学解题中的应用与实践[J].教育科学,2013,(05):196.
[2]蔡小雄.更高更妙的高中数学思想与方法(第二版)[M].浙江大学出版社,2010,(4).
[3]赵宝玲.浅谈如何激发学生学习高中数学的兴趣[J].大众文艺(快活林),2009,(24).
(责任编辑 赵永玲)

