主成分分析在疾病检测中的应用

刘桃花

(邵阳学院理学与信息科学系，湖南邵阳422000)

0 引言

疾病检测是人们日常就诊中很常见且很重要的环节，对于家庭个人检测疾病具有显著意义.其中，肝病检测是检查肝脏是否健康的一种方式，如果肝功能出现问题会影响生活质量，一般造成肝功能出现问题的原因有可能是肝病的传染造成的，也有可能是由于工作压力过大，没有很好的休息或者是由于其他疾病引起了暂时的肝功能造成问题.所以辨别肝功能是不是真正的出现问题还是要有一定的标准，所以就有了肝病检测指标.

医生对病人的诊断是靠对病人观测若干症状后来综合评定的.如一个人发高烧，医生根据他的体温高低、白血球数目及其其他症状来判断它是患感冒、肺炎还是其他疾病.为了使判断更为准确可靠，事先应有一批经专家确诊或手术后经病理化验确诊的病历资料，根据这批资料利用多元统计方法可建立诊断的准则(即专家系统).对来就诊的病人，按专家系统的要求，观测若干项指标后，根据诊断准则，即作出诊断.

在对疾病检验指标进行分析时，为了尽可能全面反映评价对象的整体情况，需要选取恰当的、客观的指标.在实际工作中，需要精简指标，将原来的指标重新组合成一组相互无关的综合指标以此来尽可能多地反映原来指标信息量，主成分分析为解决此类问题提供了很好的方法.

1 主成分分析原理

1933年，Hotelling提出的主成分分析(Principal Component Analysis)方法正是实现这一目的的有效途径之一.主成分分析是考察多个定量(数值)变量间相关性的一种多元统计方法.它的基本思想是通过降维过程，将多个相互关联的数值指标转化为少数几个互不相关的综合指标的统计方法，即用较少的指标来代替和综合反映原来较多的信息，这些综合后的指标就是原来多指标的主要成分.简而言之，主成分实际上就是由原变量X1～Xm线性组合出来的m个互不相关、且未丢失任何信息的新变量，也称为综合变量.多指标的主成分分析常被用来寻找判断某种事物或现象的综合指标，并给综合指标所蕴藏的信息以恰当解释，以便更深刻地揭示事物内在的规律［1-4〛.

适合用主成分析方法的数据应该有如下表格所示的特点:

表1 主成分分析的数据结构Tab.1 Data structure of principal component analysis

设数据具有表1的结构，且主成分为Z，表达式如下:

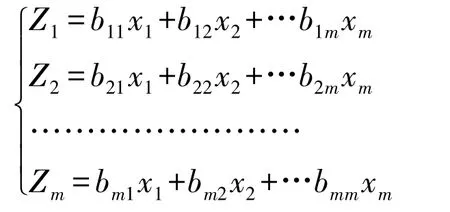
其中Xi为原始变量，xi为Xi的标准化变量(即每个原始变量减去样本均数再除以样本标准差);bij是线性组合的系数，称为因子负荷量，λi为与第i个主成分对应的特征值，i，j=1，2，…，m.

求主成分的计算过程，实际上就是求上述表达式因子负荷量.上面的表达式是由标准化变量的协方差矩阵(即相关矩阵)求特征值及其对应的特征向量，其分量为bij，i，j=1，2，…，m，SAS 中直接给出的因子负荷量与表达式对应.

主成分分析的基本条件与主成分的基本性质:

原始变量的个数为m，则系数矩阵R就是m阶方阵，特征值为λ，求各特征值λi的过程就是求解下列特征方程:|R-λi|=0，此方程的左边展开后实际上是一个λ的m阶多项式，其解由大到小依次排列为λ1≥λ2≥…≥λm＞0.主成分分析的基本条件与主成分的基本性质可概述如下:

①各主成分之间互不相关，若原变量服从正态，则各主成分之间互相独立;

②全部m个主成分所反映的n例样品的总信息，等于m个原变量的总信息.信息量的多少，用变量的方差来度量.若将m个原变量标准化后，每个变量的方差都为1，故方差之和为m，此时，求得的m个主成分的方差之和也为m;

③各主成分的作用大小是 ∶Z1≥Z2≥…≥Zm;

④第 i个主成分的贡献率是(λi/m)×100%;

2 主成分分析在肝病检测指标中的应用

以下是某医院记录的100例肝病患者的18项症状.这100名患者中，有21名女性，79名男性，其中20岁以下(不包括20岁)有6名，20岁以上且40岁以下(不包括40岁)有36名，40岁以上且60岁以下(不包括60岁)有43名，60岁以上(不包括60岁)有15名.

这18项症状分别是:输血史、低热(≦38℃)、中高热(＞38℃)、寒战、踝部水肿、胫前水肿、下肢水肿、单侧上肢水肿、巩膜黄染、皮肤黄染、肝掌、蜘蛛痣、皮肤搔痒、咯白痰、咳嗽、咽痛、扁桃体红、扁桃体肿大，依次用X1至X18表示，其中0表示无该症状，1表示有该症状.

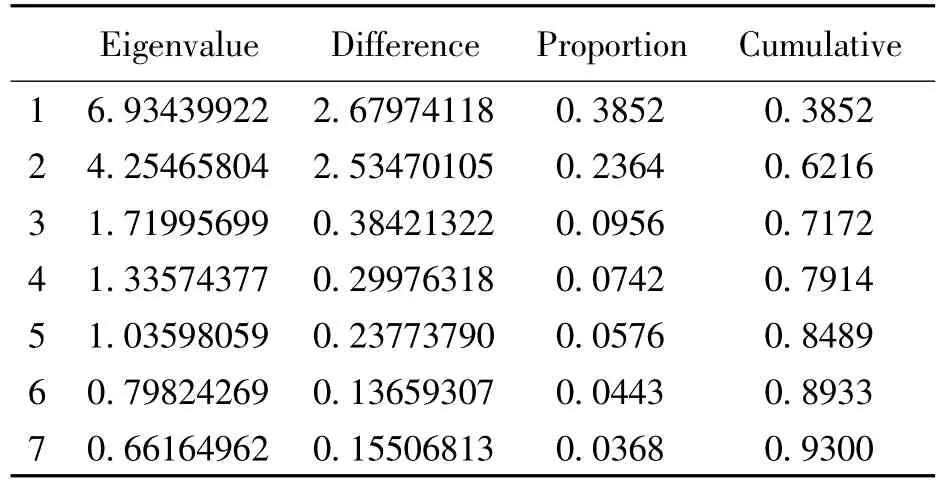
表2 相关矩阵的特征值Tab.2 Eigenvalues of the correlation matrix

我们通过SAS软件［5］对上述事例进行主成分分析，第1部分给出了相关矩阵的特征值(Eigenvalue)，(文章只给出了前7个主成分的特征值)特征值越大，它所对应的主成分变量包含的信息就越多.第1个至第7个主成分的贡献率分别为 38.52%、23.64%、9.56%、7.42%，5.78%、4.43% 和3.68%，最后1列为累计贡献率，由此列数值可知:前7个主成分就包含了原来18个指标93.00%的信息.

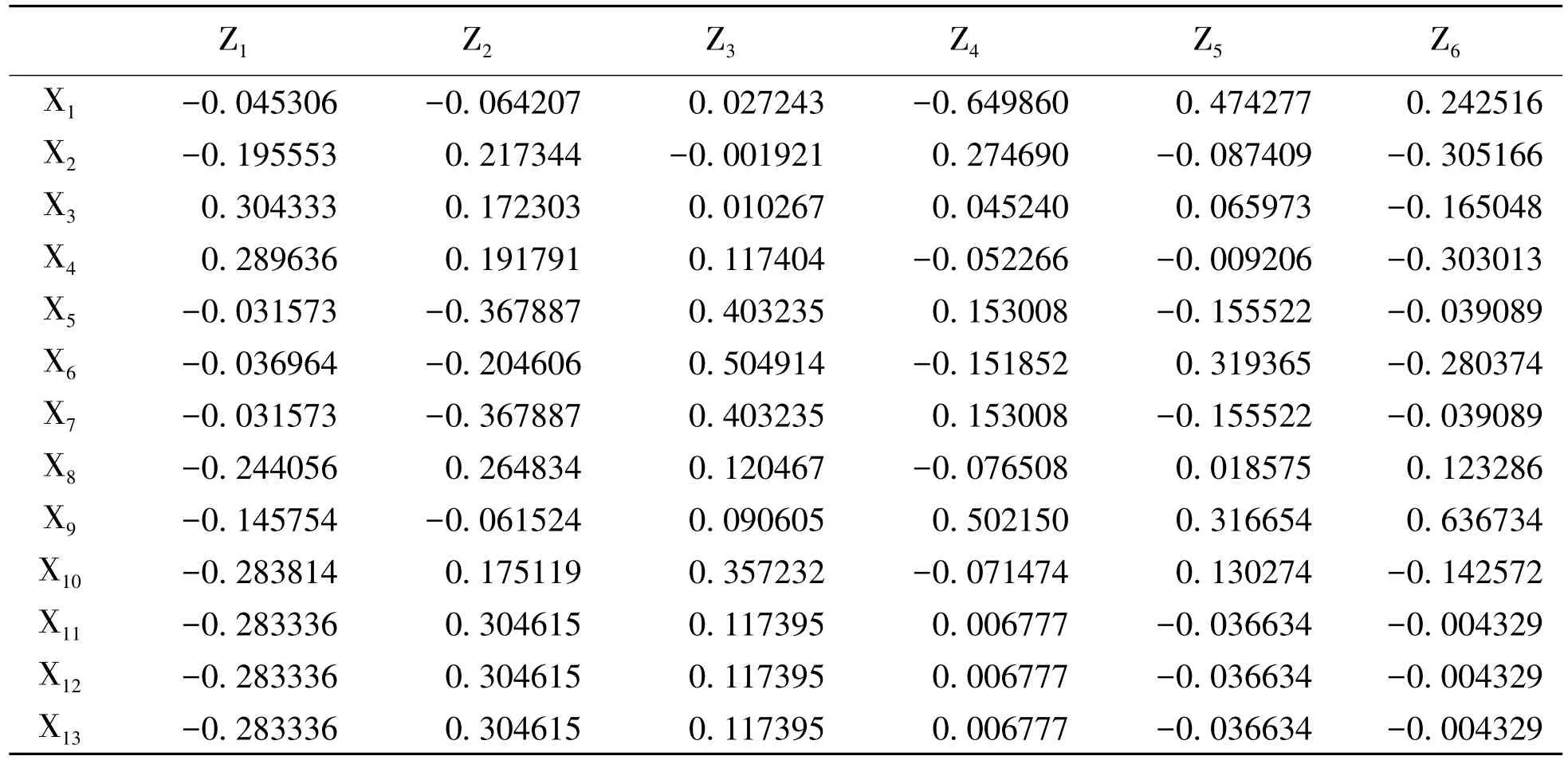
表3 特征向量Tab.3 Eigenvectors

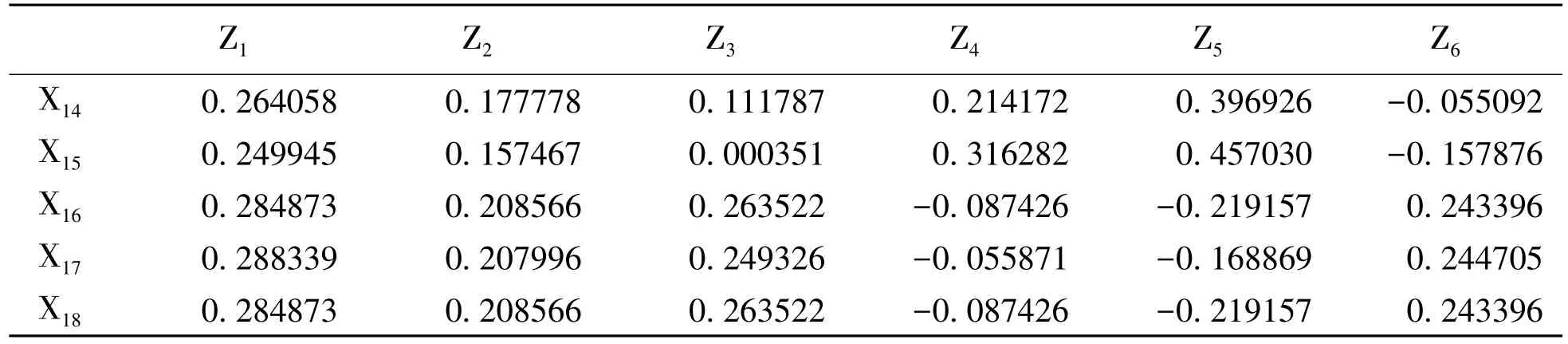
续表

第2部分给出了特征向量(Eigenvectors)，(文章只列举了前6个主成分的特征向量)，据此可以写出由标准化变量所表达的各主成分的关系式:

在各主成分的表达式中，各标准化指标Xi前的系数与该主成分所对应的特征值之平方根的乘积是该主成分与该指标之间的相关系数，如∶

系数的绝对值越大，说明该主成分受该指标的影响也就越大.因此，决定第1主成分Z1大小的主要为 X3和 X4，即中高热(＞38℃)和寒战;决定第2主成分Z2大小的主要为X5和X7，即踝部水肿和下肢水肿;决定第3主成分Z3大小的主要为X5、X6和X7，即踝部水肿、胫前水肿和下肢水肿AFP;决定第4主成分大小的主要为X1和X9、X15，但作用相反.这可以表明(以专业知识为依据):Z1指向传单;Z2指向肺炎;Z3指向丙肝;Z4指向急性乙肝，Z5指向心衰，Z6指向慢性乙肝，Z7指向乙肝，其余的贡献率很小，仅作参考，它可能指向其他肝病，如指向急性肝萎缩.

求出了主成分，并结合专业知识给各主成分所蕴藏的信息以恰当的解释，还应该利用它们来判断样品的特性，本例可据肝病患者的4个主成分值来为判断肝病类型提供参考.为了求主成分值的方便，可将用标准化指标表达的主成分换成用原指标表达的形式.

设现有一名疾病就诊者，测得18项疾病指标为:X1=0，X2=1，X3=0，X4=0，X5=0，X6=0，X7=0，X8=0，X9=1，X10=1，X12=1，X13=1，X14=0，X15=0，X16=0，X17=0，X18=0，把它们分别代入Z1至Z18表达式中计算得，Z6值最大，即第6主成分的值最大，因此，诊断该病人炎症类型很可能为慢性乙肝.

3 总结

本文通过SAS软件利用主成分分析，得出影响判断疾病的主要诊断指标，尤其是对肝病诊断，并通过患者的检测指标对其所患的肝病类型进行判断.我们通过求出主成分，并结合专业知识给各主成分所蕴藏的信息以恰当的解释，并且利用它们来判断样品的特性，据患者的18个主成分值来为判断疾病类型提供参考.

可以看出，主成分分析在指标体系中其应用前景十分广阔.近年来，主成分分析方法在社会经济问题研究中的应用越来越多，其应用范围也更加广泛.因此，我们应当正确理解和运用这种方法，使其发挥出各自最大的优势，以便于更好地服务于社会.

［1］胡良平.现代统计学与SAS应用［M］.北京:军事医学科学出版社，2000.

［2］高惠璇.应用多元统计分析［M］.北京:北京大学出版社，2005.

［3］高惠璇.实用多元统计分析［M］.北京:北京大学出版社，2006.

［4］约翰逊，威克恩.实用多元统计分析［M］.北京:清华大学出版社，2008.

［5］李东风.统计软件教程［M］.北京:人民邮电出版社，2006.