霍尔效应与新材料的发展

申莉华，周本胡，谭尚书

(1.邵阳学院理学与信息科学系，湖南邵阳422000;2.邵阳学院后勤中心，湖南邵阳422000)

0 引言

从1879年发现经典霍尔效应到2013年发现量子反常霍尔效应，人类经历了一百多年的历程，这一百多年同时伴随着许多新材料的发现和制备.新材料是一个国家经济发展的三大(材料、能源和信息)支柱之一.本文着重介绍了经典霍尔效应、量子霍尔效应和反常量子霍尔效应，以及在石墨烯、拓扑绝缘体等纳米新材料的发展过程中的应用.

1 经典霍尔效应

霍尔效应从本质上来讲是一种磁电效应.带电粒子在磁场中会受到洛伦兹力的作用，如图1所示，在导体的上下表面出现了电势差U=K·I·B/d……(1)其中K为霍尔系数，I为薄片中通过的电流，B为外加磁场的磁感应强度，d是薄片的厚度.这种现象称为霍尔效应，U称为霍尔电压.

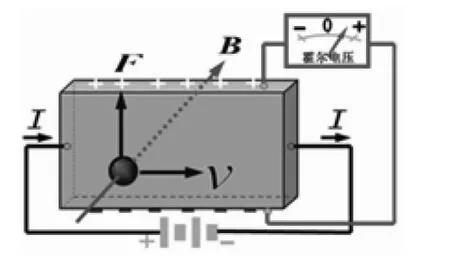
图1 霍尔效应Fig.1 Hall Effect

1.1 半导体材料

所谓半导体，就是导电能力介于导体与绝缘体之间的物质.常见半导体分有元素半导体(如 Si、Ge、灰 Sn、P 等等)和“化合物”半导体(如以 GaAs、GaN等等).半导体对微量的杂质和缺陷是十分敏感的.由上述(1)式知道，K值越大，元件厚度越小，输出电压越大.霍尔系数:K=1/(n*q)式中，其中n为载流子密度，一般金属材料中电子浓度很大，所以金属材料的霍尔系数很小，霍尔效应很微弱，所以金属导体中的霍尔效应应用价值不大.然而半导体中的载流子的密度比金属要小得多，所以半导体的霍尔系数比金属大得多，能产生较大的霍尔电压，即半导体中的霍尔效应非常显著.因此，制作霍尔元件往往采用半导体材料而非金属材料［1-2］.1948年诞生了世界上第一支用锗单晶体材料制作的晶体管，五十年代初盛行锗二极管、锗三极管，可是锗在自然界中比较稀少，要获得锗材料，必须付出较高的成本，所以推广应用锗材料存在一定的困难.人们开始寻找新的半导体材料，而这种材料应当是在自然界中大量存在并且物美价廉的，这种材料就是硅.几十年来硅半导体材料在电子技术领域中一直占有绝对优势的地位［2-3］.90年代以来随着电子科学技术的迅猛发展，作为“化合物”半导体的砷化稼和磷化铟具有许多硅所没有的优良的电学特性，在集成电路和光纤通讯方面应用很广泛.

1.2 纳米材料

所谓纳米材料又称为超微颗粒材料，由纳米粒子(nano particle)组成.纳米粒子一般是指尺寸在1～100nm间的粒子，它具有表面效应、小尺寸效应和宏观量子隧道效应.20世纪80年代人们利用纳米技术将宏观物体细分成超微颗粒(纳米级)后，它的光学、热学、电学、磁学、力学以及化学方面的性质和大块固体时相比显示出许多奇异的特征，这就是说我们可以通过直接操纵和安排原子、分子而创造新物质.其中对磁性纳米薄膜的研究较多.

磁性纳米薄膜属于低维磁性纳米材料，存在巨霍尔效应，它是制造霍尔传感器的理想材料，开辟了磁记录领域的新天地.磁传感器不易受到污染和高温环境的影响，它将是工作在特殊环境下的新一代霍尔传感器产品［4］.

磁性纳米薄膜的霍尔效应在实验和理论方面都有一定的研究，但在制备磁性纳米薄膜时基质比较单一，因此对磁性纳米薄膜的霍尔效应仍然有待进一步研究［5］.

纳米材料最大的缺点就是很难实现大批量生产，手性角变化一下就是另一种纳米材料了，所以用于制作器件的纳米材料无法大规模生产.我们期待激动人心的纳米时代早点到来.

2 量子霍尔效应

量子霍尔效应其实验是在极低温度和强磁场作用下发生的霍尔效应.其实验图像和经典的霍尔效应基本上相同，不同的是我们测得的霍尔电导是一个个分立的值，而不是连续的值，而且随外加磁场的变化呈现一种振荡的变化，这个就是量子霍尔效应.量子霍尔效应是体系态密度在磁场作用下量子化的结果，只能在量子力学的框架下解释.量子霍尔效应中对量子电导有贡献的是边界态，也就是说导电电子是在材料的边界上走的.在二维体系中，边缘出现的霍尔电导将是由块体拓扑保护的，通过Chern数或绕数分析可以得到以e2h-1为单位的量子霍尔电导.

1980年，克利青等人在二维体系的霍尔效应实验中，多次研究在处于极低温度(1.5K)和强磁场(18T)的作用下，发现了一个与经典霍尔效应完全不同的现象:其霍尔电阻RH随磁场的变化出现了一系列量子化平台，这种现象称为整数量子霍尔效应［4］.

1982年，崔琦等人在比整数量子霍尔效应更低的温度0.1K和更强的磁场20T条件下，对具有高迁移率的更纯净的二维电子气系统样品的测量中，也在一些电阻和温度范围内观测到横向霍尔电阻呈现平台的现象，但不同的是，这些平台对应的不是整数值而是分数值，称为分数量子霍尔效应［4-5］.

自旋量子霍尔效应:和霍尔效应一样，电子在边界上移动.不需要磁场，但材料需要有强的自旋轨道耦合，而有强自旋轨道耦合将导致能带反转.在二维体系的表面边缘将出现自旋电流，上下自旋电流反向传播，所以没有电荷电流，也没有霍尔电导.但是这两种沿不同方向传播的电子自旋方向相反，有一个净的自旋流，而且类似于经典霍尔效应，这个自旋流的自旋电导也是量子化的，因此称为自旋量子霍尔效应［6］.

2.1 石墨烯材料

英国物理学家安德烈·海姆和康斯坦丁·诺沃肖洛夫于2004年发现了石墨烯(Graphene).石墨烯，又名单层石墨，只有一个碳原子的厚度，它是从石墨材料中剥离出来的一种由六角形蜂巢晶格排列的碳原子组成的平面薄膜［6］.

石墨烯特有的能带结构使空穴和电子相互分离，导致了石墨烯的电子运输特性，它表现出了异常的整数量子霍尔效应.其霍尔电导为量子电导的奇数倍，且可以在室温下观测到.

在铁磁石墨烯体系中存在一种新类型的量子自旋霍尔效应，这量子自旋霍尔效应与自旋轨道耦合无关.另外，除了量子自旋霍尔效应之外，该体系也可能有量子霍尔效应，从而纵向电阻和霍尔电阻都呈现平台结构.特别是，由于体系受CT不变所保护，自旋霍尔电阻的量子化平台有很强的抗杂质干扰能力.

科学家发现，石墨烯还是目前已知导电性能最出色的材料，它在室温下传递电子的速度比已知导体都快.石墨烯在太阳能电池、传感器方面、纳米电子学、高性能纳米电子器件、复合材料、场发射材料、气体传感器及能量存储等领域将具有广泛的应用.当然目前关于这方面的理论研究开展的如火如荼，但是距离应用仍然还有相当的距离，有待于实验工程方面进一步的研究.

2.2 拓扑绝缘体材料

拓扑绝缘体是最近几年发现的一种全新的物质形态，目前已经引起了巨大的研究热潮.它的体材料是有能隙的绝缘体，但其表面或边缘是无能隙的金属态.拓扑绝缘体的基本性质是由“量子力学”和“相对论”共同作用的结果，由于自旋轨道耦合作用，在表面上会产生由时间反演对称性保护的无能隙的自旋分辨的表面电子态［7］.由于这些态受时间反演对称性保护，不易受到杂质和无序的影响，它们由无质量的狄拉克(Dirac)方程所描述，而不能用薛定方程描述.在实际拓扑绝缘体材料中，想得到分数化的量子霍尔电导可能是很困难的.量子自旋霍尔效应出现在具有体带隙两边螺旋边缘态能带交叉于该带隙的二维拓扑绝缘体中.

据我了解，拓扑绝缘体与石墨烯相比，拓扑绝缘体的理论性要强一些，石墨烯和碳纳米管只是几种材料而已，而拓扑绝缘体是一个类型，是自旋量子霍尔效应在表面造成的性质.拓扑绝缘体与量子霍尔效应、量子自旋霍尔效应等领域紧密相连，其基本特征都是利用物质中电子能带的拓扑性质来实现各种新奇的物理性质.特别是，数值计算表明这样的自旋霍尔电阻化平台在宏观尺度上也能保持.所以其更好地反映了自旋量子霍尔效应的拓扑本质.

低维拓扑绝缘体表面态有一个内在的净角动量或自旋，该净角动量或自旋因体能带的拓扑结构而受到保护，不会因无序等因素而发生散射，这正是人为操控电子自旋非常想得到的一个性能，为设计制造全新概念的电子器件提供理论依据.

3 反常量子霍尔效应

1880年，霍尔在研究磁性金属的霍尔效应时发现，即使不加外磁场也可以观测到霍尔效应，这种零磁场中的霍尔效应就是反常霍尔效应.

2013年，即在美国物理学家霍尔发现反常霍尔效应133年后，中国科学家首次在实验中观测到反常霍尔效应的量子化［8］.反常量子霍尔效应也是电子自旋-轨道耦合的结果，在新的稀磁半导体材料和自旋电子学材料中应用极广.为了更好地表征这些铁磁材料的内禀性质，需要人们更深入地研究反常霍尔效应的机制，这引起了很多理论工作者的兴趣.然而，结合第一性原理计算方法，建立一套系统的理论体系来令人信服地解释螺旋散射、边跳等外在机制与内禀机制的所有争论，还需要进一步的研究［9］.

在拓扑绝缘体材料(Bi2Se3，Bi2Te3 and Sb2Te3)薄膜中通过掺杂过渡金属元素(Cr或者Fe)可以实现量子化的反常霍尔效应［10］.这一发现，为设计低能量耗散的新型电子器件指出了一个新的方向.今后，基于量子反常霍尔效应制成的新型电子器件，或许会取代我们现在使用的这些半导体器件，使信息技术进入一个崭新的时代.

［1］刘恩科，朱秉升，罗晋生.半导体物理学［M］.北京:电子工业出版社，2010.

［2］李翔，曹灿华，翟堃，乔荣学.半导体材料的浅释［J］.科技传播，2011，(3):154-155.

［3］林耀望，朱素珍.加速我国半导体材料的发展［J］.材料导报，1987，(4):1-6.

［4］张海涛.霍尔效应及应用［J］.温州职业技术学院学报，2005，(12):26-28.

［5］刘雪梅.霍尔效应理论发展过程的研究［J］.重庆文理学院学报(自然科学版)，2011.(4):41-44.

［6］孙庆丰，谢心澄.铁磁石墨烯体系的CT不变量子自旋霍尔效应［J］.物理，2010，39(6):416-418.

［7］常 凯.拓扑绝缘体电子态的电场调控［J］.物理，2011，(7):458-461.

［8］梁拥成，张英.反常霍尔效应理论的研究进展［J］.物理，2007，(5):385-390.

［9］张金松.发现量子反常霍尔效应［J］.科学世界，2013，(6):80-81.

［10］余睿，张薇，翁红明，戴希，方忠.磁性拓扑绝缘体中的量子化反常霍尔效应—无需外磁场的量子化霍尔效应［J］.物理，2010，(09):618-623.