基于粒子群优化的移动通信功率控制方法

夏太武

(邵阳学院信息工程系，湖南邵阳422000)

0 引言

在移动通信系统中，不同业务在传输速率、误码率和时延要求等方面存在差异，而用户信号功率和传输速率的分配直接决定着系统容量和频谱利用效率［1-2］.功率控制技术是目前移动通信中最为关键的技术之一，它不仅可以克服远近效应，而且可以减少用户间的多址干扰(MAI)，其目的是为了实现通信质量最佳化和系统容量最大化［3-4］.常用方法有分布式平衡算法、自适应步长功率控制算法和信息论方法等［5-6］，这些方法均存在计算操作繁复，不易获得全局最优解等缺点，对此已有相关人员在研究探讨遗传算法(GA)、粒子群算法(PSO)等进化计算方法［7-8］，而PSO算法以其简单、容易实现且没有许多参数需要调整等优势，已广泛应用于诸多领域［9］.本文在分析和探讨CDMA通信系统的功率控制模型基础上，采用改进的PSO算法进行功率控制模型的优化，可提高功率控制效果，且更加符合实际情况.

1 功率控制模型建立

假设某小区的DS-CDMA移动通信系统中有N个用户，他们共享相同的扩频带宽W，但不同用户有不同的传输速率、误码率和时延等要求.为分析方便本文将将误码率要求映射为目标比特能量噪声比Eb/No，将时延要求映射为用户具有一定范围内可变的传输速率，另每个用户还有最大发射功率Pmaxi和最小传输速率Rmini的约束.令用户i到其所属基站接收机的信道增益为hii，用户j到用户i所属基站接收机的信道增益为hij，用户i的信号发射功率为Pi，目标 Eb/No为 γi，基站接收机处背景噪声为单边功率谱密度为η0的加性高斯白噪声，那么基站接收到用户 i信号的 Eb/No为［1］:

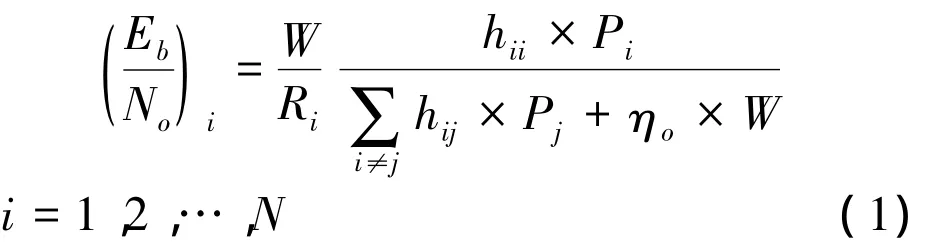
根据总发射功率最小化的优化准则，并同时考虑降低不同小区间用户的干扰，该优化问题的模型为:

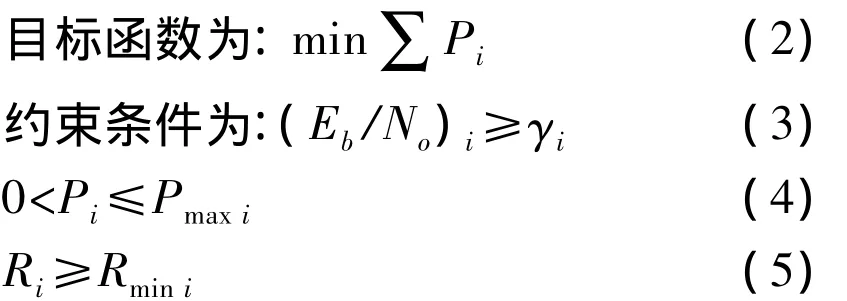
上述基本功率控制模型中将所有用户视为同等优先级，这种“平等对待”的策略不能满足系统处在重负荷时对服务质量(QoS)要求特别严格或必须保证的业务需求，如话音业务就有可能被中断，而此时系统应该考虑可以通过牺牲那些QoS要求不高的业务的传输质量来保证话音类业务的正常传输，即应该有业务优先级划分的控制策略.

为此，在功率分配上采用优先级系数Ai来表示优先级情况，则改进的功率控制模型如下:

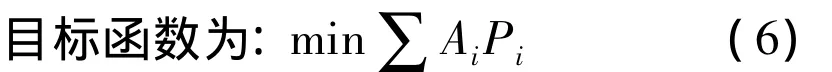
约束条件仍为式(3)～(5).

2 采用改进PSO优化功率控制模型

2.1 一种改进的PSO算法

粒子群优化(PSO)算法是基于群智能的进化算法，首先初始化为一群随机粒子，然后通过多次迭代找到其最优解.每次迭代中可通过跟踪个体极值pbest和全局极值gbest来更新粒子的速度和位置，为加快算法的收敛性，可采用一种具有梯度搜索因子的Grad-PSO算法［9］，其速度和位置更新公式如下:

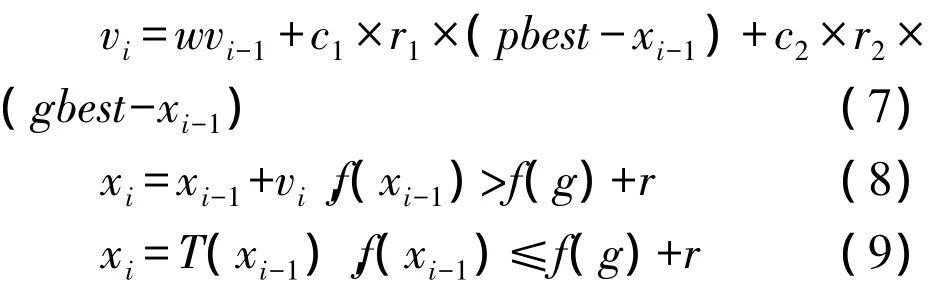
这里，vi，vi-1分别为当前和上一次的粒子移动速度;xi，xi-1分别为当前和上一次的粒子的位置;w为惯性权重;r1，r2为0～1间的随机数，c1，c2为学习因子.

若粒子群的适应度函数f(x)在g点取极值，则在以g点为圆心，半径为r的圆内采用式(9)所示的梯度法进行位置更新;在圆外区域仍采用式(8)进行位置更新.这样一方面可减轻随机更换位置所带来的时间负荷;同时另一方面也提高了寻优效率.

为此本文提出了基于改进PSO算法的功率控制方法，即采用上述改进的PSO算法对基本功率模型(式(2)至式(5))和改进的功率控制模型(式(6)、式(3)至式(5))进行寻优求解.

2.2 仿真实验

根据功率控制模型式(6)和约束条件式(3)～(5)，设某CDMA移动通信系统中的有关参数为:N=2，i=1，2;P1=x1，P2=x2，R1=y;W=100MHz，η0=5×10-8，h11=3，h12=2，h21=2.4，h22=2.5，γi=0.5，Pmax1=Pmax2=1W，Rmini=50kbps，优先级系数 A1=10，A2=100.则具体数学模型为:

下面采用改进的PSO算法进行求解，其中参数设置为:种群规模为m=20，最大迭代代数Gmax=100，惯性权重w依据Gmax从0.9 线性递减至 0.1;c1=2;c2=2;r1、r2随机产生;最优区域半径r=0.03.

图1和图2分别为采用PSO求解的两种功率控制模型对应的离线性能曲线.图1中当优先级系数A1=A2=1时，PSO迭代寻优至30代时获得最优解x1=0.5208，x2=0.6250，此时 f(x1，x2)=1.1458;图 2 中当优先级系数 A1=10、A2=100时，PSO迭代寻优至28代时获得最优解x1=0.5208，x2=0.6250，此时 f(x1，x2)=67.7083.对比上述两图可知，无论对于基本功率控制模型，还是改进的功率控制模型，在采用PSO算法寻优过程中，都是随着迭代代数的增加而趋于最优解，两者均在迭代代数为30左右时即能获得最优解.说明采用PSO算法是切实可行的，且优化效果显著;此外从保证高优先级业务的传输质量上看也验证了改进后的功率控制模型更符合实际情况.

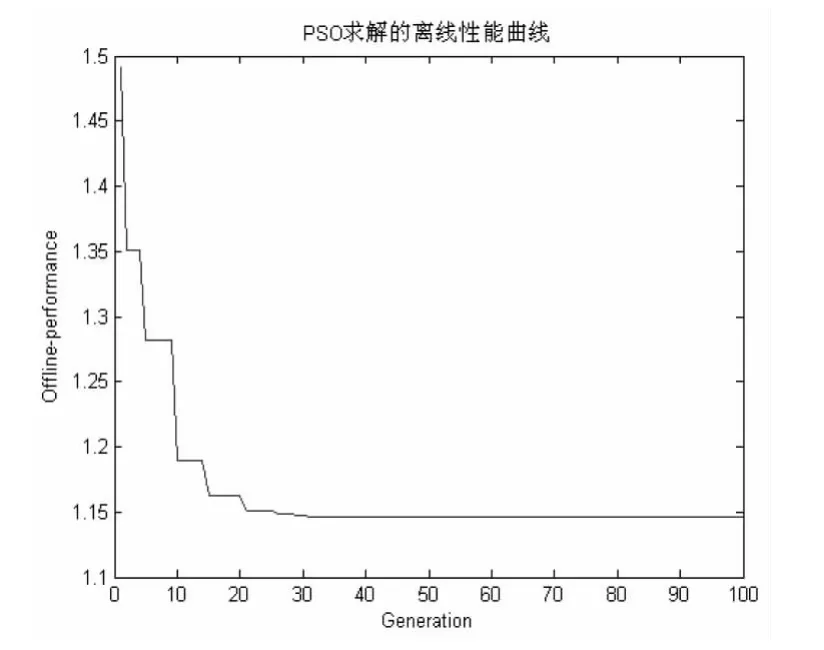
图1 PSO迭代寻优曲线(A1=A2=1)Fig.1 PSO iterative optimization curve(A1=A2=1)

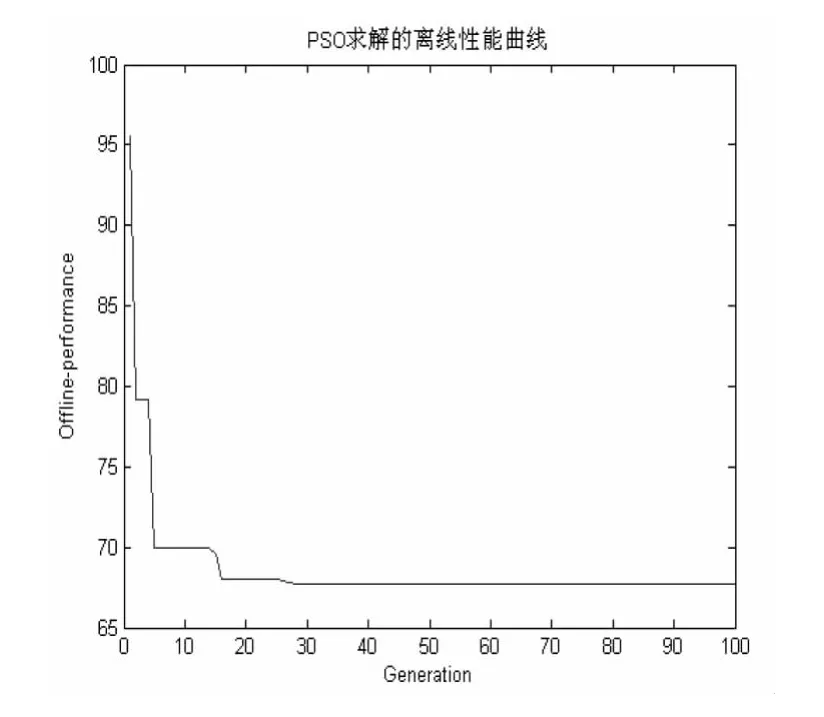
图2 PSO迭代寻优曲线(A1=10，A2=100)Fig.1 PSO iterative optimization curve(A1=10，A2=100)

3 结论

本文在分析和探讨移动通信的功率控制模型基础上，提出基于改进PSO算法的功率控制技术，仿真实验表明，采用改进的PSO算法进行寻优求解，可以完成功率控制，并能较大地提高工作效率.另外使用改进后的功率控制模型在应用中更符合实际情况.

［1］王宇，李少谦，李乐民.CDMA蜂窝移动通信系统中的联合功率控制［J］.电子学报，2000，28(11):114-118.

［2］Amaladi E，KannV.The complexity and approximability of finding maximum feasible subsystems of linear relations［J］.Theoretical Computer Science，1995，147(2):181-210.

［3］M.Zhang，T.P.Yum.Comparisons of Channel Assignment Strategies in Cellular Mobile Telephone Systems［J］.IEEE Trans.Veh.Technol，1989，38(4):211-215.

［4］尚松蒲，胡晓东，李旭.移动通信系统中的最优功率控制算法［J］.应用数学，2006，19(1):100-110.

［5］党安红，朱世华，汤俊雄.蜂窝移动通信系统中的一种分级紧致的动态信道分配方案［J］.通信学报，2002，23(9):42-48.

［6］龙昊波，赵永贵，孙宇，等.基于三层C/S结构的隧道TSP信息管理系统［J］.计算机工程与应用，2006，42(3):230-232.

［7］赵亚敏，许家栋.一种改进的微粒群优化算法［J］.计算机工程与应用，2010，46(2):31-33，21.

［8］张坤，吴跃.PSO算法在通信基站分布规划中的应用［J］.计算机与数字工程，2006，34(6):135-138.

［9］曹国华，李婷婷.改进PSO算法及其在函数优化中的应用［J］.南京师范大学学报(工程技术版)，2007，7(2):10-13.