约束条件下大小胶球尺寸比值对排空作用的研究
邓元祥
(湖南工学院数理教学部,湖南衡阳421002)
0 引言
胶球间的排空作用是目前学术界炙手可热的研究问题之一.Asakura和Oosawa最早提出了排空作用这个概念,他们认为在小粒子的流体中大粒子之间存在排空作用[1].近些年来,随着对该课题的深入研究,已经通过理论分析、实验测试以及计算机模拟等手段,获得了许多有关排空作用的性质和特征信息.其中,对无约束条件下大胶球间的排空作用的信息较为全面,但是对几何约束下排空作用的认识还刚刚起步.显然,几何约束的情形是多种多样的,因此约束条件下的排空作用也与实际应用有着更为广泛的联系,因而需要更为详细的研究.目前,人们已经研究了单边硬板限制时大胶球的排空作用[2-3],同时,在曲面限制时大胶球的排空作用也有相关的报道[4-6].我们自己研究了在非约束情形下大小胶球不同尺寸比的排空作用[7],本文在此基础上进一步研究在有两块平行硬板限制时,随着大小粒子半径比值发生改变,对大粒子之间的排空作用进行研究,即主要考虑在限定尺寸范围内的粒子尺寸的变化对排空作用的影响.
1 模型及计算方法
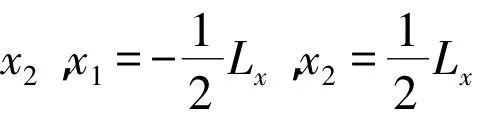
根据自由能差的公式
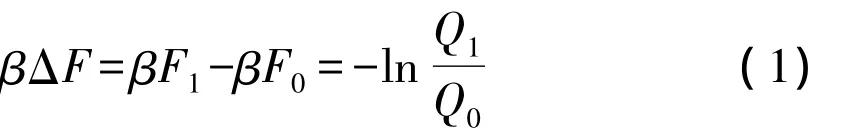
式中 β=(kβT)-1,kβ是波尔茨曼常数,T 为温度.加入权重函数W(r),两个系统配分函数[11]比值可以写成
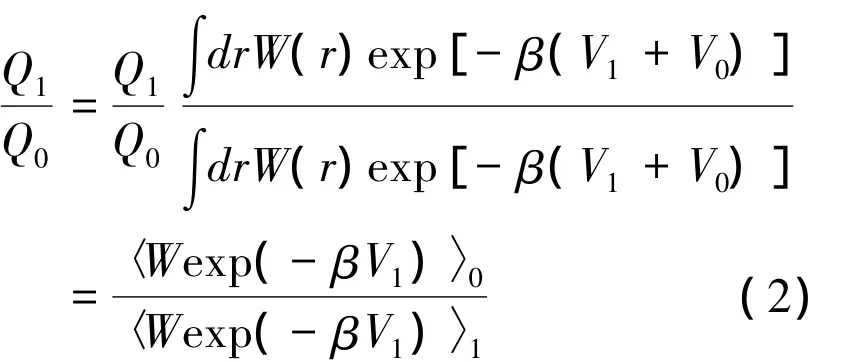
式中r表示体系中胶球的坐标,下标0、1分别表示V0、V1体系的统计平均.权重函数可以写成如下简洁的形式
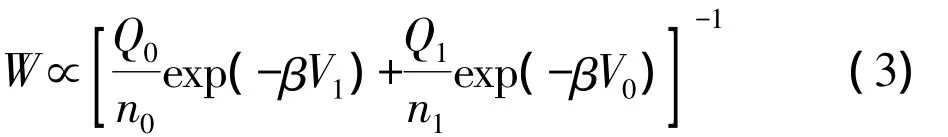
式中n0和n1是两个待定常数.将(3)式代人(2)式中,式(2)写为
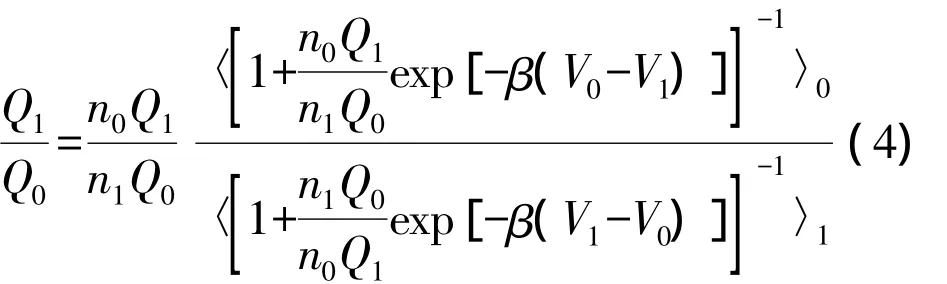
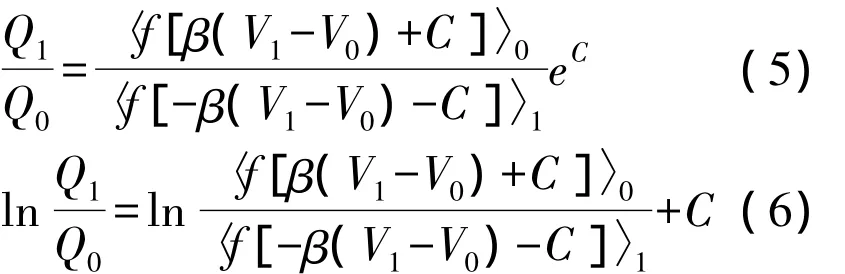
上式中f(x)=[1+exp(x)]-1是费米函数,C是常量.对于硬球势或近似硬球势,取C=0,联合(1)式可以得到
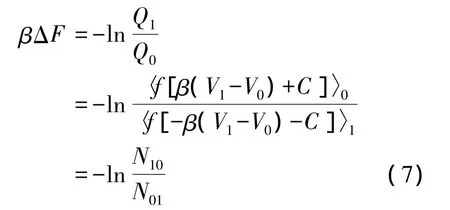
代入相关参数,可以计算出系统的排空势和排空力[5].
2 计算结果与讨论
本工作采用Monte Carlo方法和接受率方法对模型进行了计算机模拟研究,为了便于结果的对比,本文所考虑的系统参数与文献[7]中无约束情形的参数完全一样,因此,在本文中考虑体积分数为 η=0.1,0.2的两种系统,每一个系统大小胶球的半径比值为 R/r=1,3,5,7,为了突出显示大小胶球的半径比值不同时的排空作用,当R/r=1 时,取 Lx=12r,当 R/r=3,5,7时,Lx取 Lx=12r,20r,28r.同时,为了确保模型有足够大的空间,每一种胶球系统,取Lz=38r,Ly=20r.我们首先确定胶球的初始位置,即给定 η,Lx,Ly,Lz值,然后根据接受率方法对小胶球进行抽样处理[12].其中,在方向上,确定边界条件为,一旦小胶球跑出边界,即让它回到原来的位置;在Ly,Lz方向上,我们就采用周期边界条件,这就是约束条件下胶球间的排空作用系统.在计算过程当中,小胶球的移动接受率参数区间为:0.3~0.5;同时,为了使系统在计算时达到平衡,蒙特卡罗步取为:1.0×105个,为了能够完整收集数据,蒙特卡罗步取为:3.0×105个.
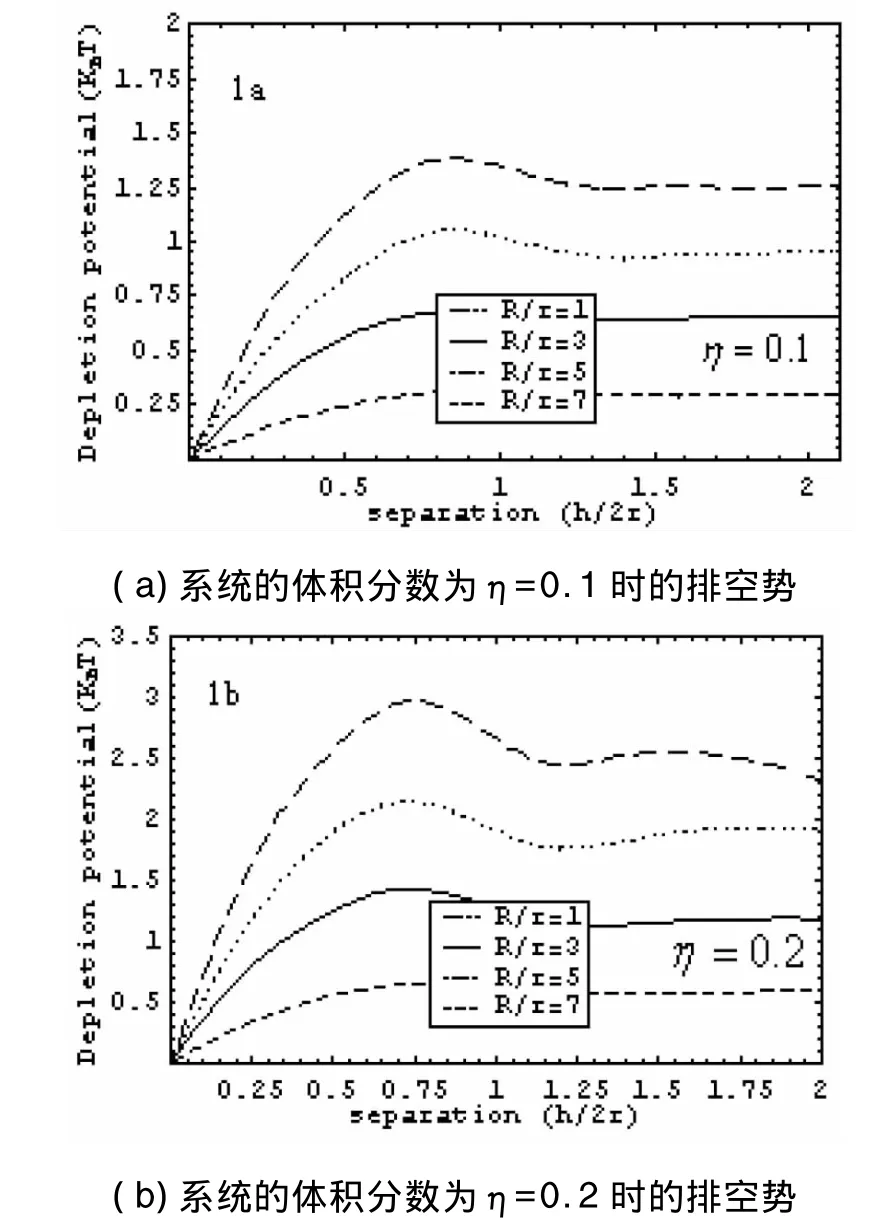
图1 两种体积分数情况下的排空势结果Fig.1 Depletion potential results of two volume fraction situations
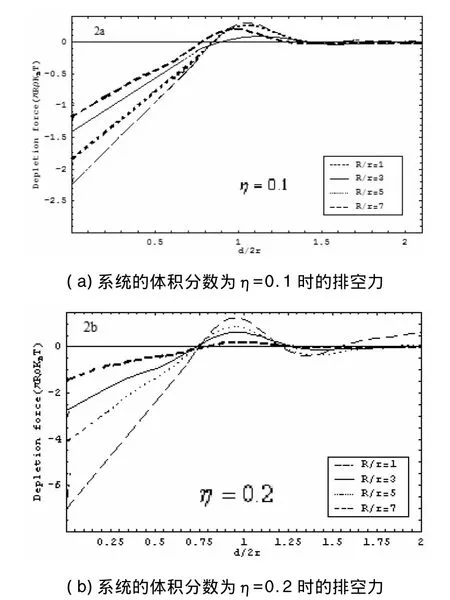
图2 两种体积分数情况下的排空力结果Fig.2 Depletion force results of two volume fraction situations
对于 η=0.1,0.2 两种体积分数情况下的排空势与排空力结果见图1、2.图示中排空势、排空力的单位分别为 KBT,πRρKBT,其中ρ是数密度,横坐标的单位取2r(r为小胶球的半径);其中,长虚线、点线、实线和短虚线分别表示大小胶球半径为R/r=1,3,5,7 时系统的排空作用.通过图 1(a)、图2(a)可知,当体积分数η=0.1时,大胶球间的排空势和排空力随着大小胶球半径比值增加而增大;同时,通过图1(b)、图2(b)可知,当体积分数η=0.2时也同样能得到大胶球间的排空势和排空力随着大小胶球半径比值增加而增大的结论.与此同时,通过对比图2(a)、(b)可知,体积分数η=0.2时,在半径比相同的情况下大胶球间的排空力明显大于体积分数η=0.1时的情形.另外,我们还将文献[7]无约束情况下粒子尺寸的变化对排空作用的结果也图示于图3(a)、(b)中.对比图2与图3,结果清楚表明,在体积分数相同的情况下,有约束时大胶球间排空作用大于无约束的情形.
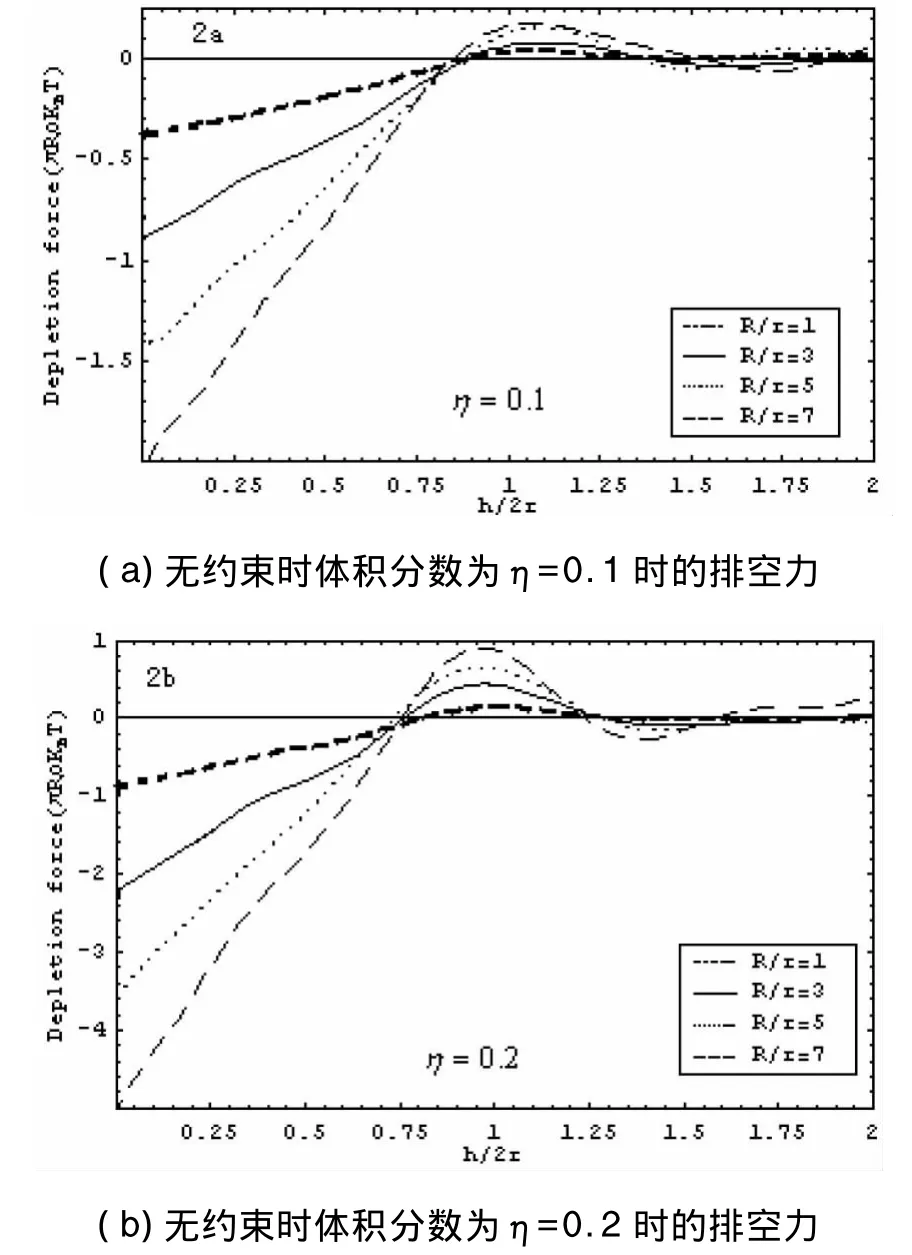
图3 无约束情况下粒子尺寸的变化对排空作用的结果Fig.3 Depletion results by the change of particle size in unconstrained situations
3 结束语
本工作通过用Monte Carlo方法和接受率方法,对处于两块平行硬板约束时半径比值分别为R/r=1,3,5,7等四种情况下的大小胶球系统进行了模拟,研究结果表明,大小胶球的半径比值对排空力有很大的影响,在体积分数相同的情况下,大胶球间的排空作用随着半径比值增加而增大.此外,通过与无约束情况下粒子尺寸的变化对排空作用的影响相比较,有约束情况下大胶球间排空作用大于无约束的情形.
[1]Asakura S,Oosowa F.Surface tension of highpolymer solution[J].J.Chem.Phys,1954,22(7):1255-1256.
[2]Li W H,Xue S,Ma H R.Depletion potential of colloids:a direct simulation study[J].Journal of Shanghai Jiao tong University,2001,6(2):126-130.
[3]Dickmann R,Attard P,Simonian V.Entropic forces in Binary hard sphere mixtures:theory and simulation[J].J.Chem.Phys,1997,107(1):205-213.
[4]Li Wei hua,Ma H R.Depletion potential near curved surfaces[J].Phys.Rev.E,2002,66(6):061407-061413.
[5]Li W H,Ma H R.Depletion force and torque on an ellipsoid[J].J.Chem.Phys,2003,119(1):585.
[6]Li W H and Ma H R.Entropic interactions on a colloidal sphere near the edge of a terrace[J].Eur.Phys.J.E.2003,12(2):321.
[7]黄立新,邓元祥,肖长明.大小胶球尺寸比值对排空作用的影响[J].湖南师范大学自然科学学报.2009,32(1):44-46 .
[8]Guo Ji yuan,Li Chun shu,Xiao Chang ming.Effect of geometrical confinement on depletion interactions in colloidal suspensions[J].Chin.Phys.Lett,2005,22(5):1267-1269.
[9]Chang ming Xiao,Jiyuan Guo,Chunshu Li.Depletion forces in colloidal system under geometrical confinements[J].Eur.Phys.J.E,2006,73(3):443.
[10]Xiao Chang ming,Jin Guojun,Ma Yuqiang.Packing effect of excluded volume on hardsphere Colloids [J].Chin.Phys.Lett.2001,18(7):950.
[11]D.Frenkel and B.Smit.Understanding Molecular Simulation:From algorithms to applications[M].NewYork:Academic Press,1996:165-193.
[12]Metropolis N,Rosenbluth A W,Rosenbluth M N,Teller A N,Teller E.Equation of State Calculations by Fast Computing Machines[J].J.Chem.Phys,1953,21(6):1087-1092.

