关于共建项目最优采购年度的层次分析

陈冀生，周 蜀，罗 剑

(重庆理工大学财务处，重庆 400054)

1 问题的提出

层次分析法(analytic hierarchy process，AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次模型，进行定性和定量分析相结合的决策分析方法［1-5］。该方法是美国运筹学家A.L.Saaty于20世纪70年代基于网络系统理论和多目标综合评价方法提出的一种层次权重决策分析方法。

实例 某高等院校在2008—2011年连续4个年度获得“中央支持地方高校发展共同建设项目资金”(以下简称“共建项目”)，需要分析总结共建项目的实施情况，其中一个重要分析点是比较“最优采购年度”。专家组根据项目资金下达后到完成采购付款的工作数据，选择年度计划金额P1(少为优)、论证确定采购计划时间P2(少为优)、申报采购计划时间P3(少为优)、分类采购计划个数P4(均值为优)、选择采购方法种数P5(均值为优)、采购付款完成时间P6(少为优)、项目完成总时间P7(少为优，设定项目资金下达后12个月内完成采购付款为合格基准数)等7个主要因素，提取基本数据(见表1)，按照满分100、比例为P1∶P2∶P3∶P4∶P5∶P6∶P7=(10∶15∶15∶10∶10∶20∶20)的统一标准计算得到分析数据(见表2)。

表1 基本数据

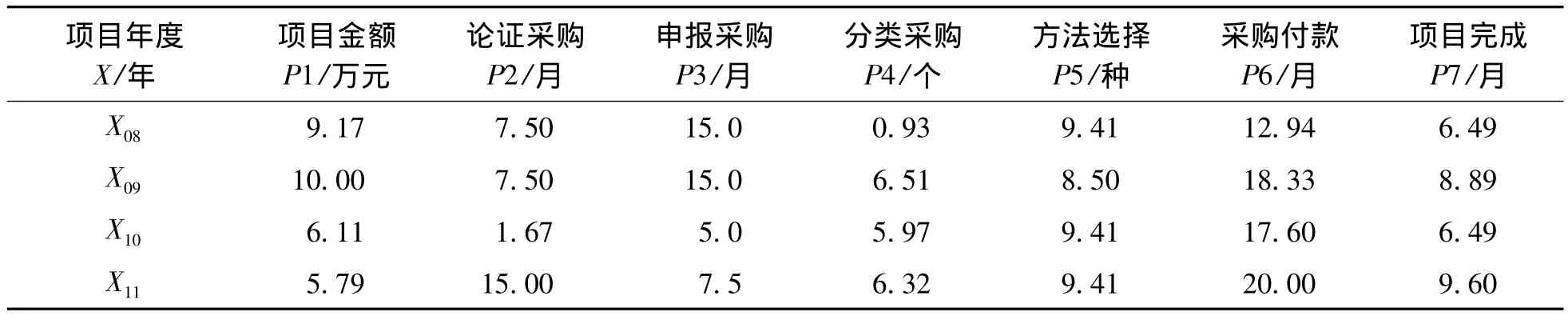
表2 分析数据

针对本例，选用AHP法分析共建项目最优采购年度，再与常用方法进行比较。

2 用AHP法分析共建项目最优采购年度

2.1 建立层次分析结构模型

首先分析本例，将有关因素自上而下分为3层:①目标层 O:最优采购年度(第1层1个元素);②准则层P:采购因素(第2层7个元素);③方案层X:项目年度(第3层4个元素)。建立采购绩效的层次分析结构模型(见图1)。

图1 层次分析结构模型

于是，问题归结为4个备选方案、7个准则定位，通过层次递进计算优先权重，然后选择唯一目标(最优采购年度)。

2.2 构造成对比较阵

1)准则层对目标层的成对比较阵(1个7阶方阵):

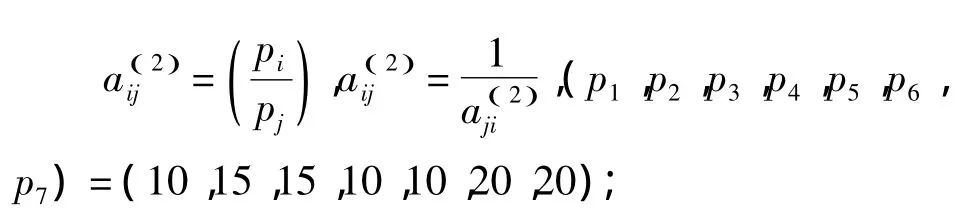
2)方案层对准则层的成对比较阵(7个4阶方阵):

2.3 计算权向量并做一致性检验

根据成对比较阵A，计算最大特征根λ和特征向量。可以验证 A 满足:aij× ajk=aik，i，j，k=1，2，…，n)，所以A是一致阵(成对比较完全一致的正互反阵)，因此具有3个性质:①A的秩为1，A的唯一非零特征根为n;②A的任一列向量是对应于n的特征向量;③ A的归一化特征向量可作为权向量。因此计算最大特征根和特征向量可以简化为:特征根λ=n，特征向量是列向量，不用再计算。

注意:本例中A是一致阵的性质很重要。笔者曾在文献［6］中指出:如果量化数据采用统一标准给出，那么成对比较阵A为一致阵，可以简化计算，并且省略一致性检验。

下面计算权向量。因为A是一致阵，所以A的列向量是特征向量，归一化即为权向量，并且具有一致性。于是计算得到2组权向量:

1)准则层对目标层的权向量w(2)=由一致阵 A(2)=，计算得权向量 w(2)=(0.1，0.15，0.15，0.1，0.1，0.2，0.2)T。

2)方案层对准则层的权向量W(3)=由一致阵，计算得7 组权向量:

2.4 计算组合权向量w并做一致性检验

根据w=W(3)w(2)，计算方案层X对目标层O的组合权向量:

得 w=(0.225 2，0.283 7，0.199 9，0.291 2)t，且，得到表3。因为A是一致阵，所以w具有一致性，检验省略。

表3 组合权向量

2.5 分析“共建项目”最优采购年度

组合权向量w确定了4个采购年度与最优采购年度的接近程度及差异度，因此权重大者优。分析表3得:X11＞X09＞X08＞X10，X11的权重最大，因此，在共建项目的4个采购年度中，最优采购年度是2011年度，次优是2009年度且与2011年度差距很小，为2.6%。通过分析基础数据表可知，此结论合理。

注意:由于最大值与最小值的差距高达45.7%，因此需要重视分析年度共建项目采购差距的具体原因，总结经验改进工作。

同样的，如果进一步分析年度共建项目中各项目单位的采购绩效，或者分析各项目的使用绩效，可以根据项目单位的采购数据、项目的使用数据，用AHP法去分析共建项目的最优采购单位、最优使用单位、最优使用项目，为后续共建项目提供必要的科学数据。

3 方法比较

3.1 综合比较法

表4 S综合法计算结果

比较 S，因为X09＞X11＞X08＞X10，X09的权重最大，因此“共建项目”的最优采购年度是2009年度，次优是 2011年度，并且两者差距很小，为1.5%。此结论与AHP法不一致。

表5 F综合法计算结果

比较 F，因为X11＞X09＞X08＞X10，X11的权重最大，因此“共建项目”的最优采购年度是2011年度，次优是 2009年度，并且两者差距很小，为1.1%。此结论与AHP法一致。

显然S、F法计算十分简单，但结论不具有一致性，因此要科学分析最优采购年度，还需借助其他分析方法。

3.2 方法比较

用综合比较法选择最优采购年度，分析计算非常简单、评选快捷，但对备选方案的比较分析粗略单一，主要分析数据只做初步统计，缺乏系统的比较，结论不具有一致性。因此，综合比较法分析此类问题不是最佳，在应用于“数据相近、因素较多、特别是定性定量指标选择与转化复杂”的问题时，难以科学区分、合理选择。

用AHP法选择最优采购年度，分析计算相对复杂，但对备选方案的比较分析具有层次清晰、全面精准、系统性强、结论唯一的优点。因此，AHP法是一种定性与定量相结合的优秀分析方法，特别是针对定性因素起主导作用的复杂问题，更加科学合理实用。如果能得到专家组的统一标准数据，则用简化的AHP法分析问题和选择最优将更加简单快捷和科学实用。

［1］Saaty T L.The Analytic Hierarchy Process［M］.USA:McGraw-Hill Company，1980.

［2］张述林;田万顷.基于AHP的旅游资源评价与发展对策研究——以重庆环城游憩带为例［J］.重庆师范大学学报:自然科学版，2011(2):70-74.

［3］王莲芬，徐树柏.层次分析法引论［M］.北京:中国人民大学出版社，1990.

［4］姜启源，谢金星，叶俊.数学模型［M］.3版.北京:高等教育出版社，2003.

［5］毛霞，王韵.基于主成分分析的高校辅导员工作实证研究［J］.重庆师范大学学报:自然科学版，2013(3):134-138.

［6］陈冀生，罗卫.用层次分析法优选供货商［J］.重庆理工大学学报:自然科学版，2011，26(12):120-124.

(责任编辑刘 舸)