锂离子电池健康预测方法
高安同,陈荣刚
(陆军军官学院,合肥 230031)
锂离子电池在应用过程中一旦发生故障,将直接导致用电设备无法正常工作,并带来高额的维修及更换费用,甚至由于过热和短路导致灾难性的爆炸事故,所以研究锂离子电池健康预测方法,优化锂离子电池维护技术势在必行。通常,锂离子电池的健康预测主要是指通过对电池工作过程中表现出的电压、电流、温度等数据进行综合分析[1]来确定电池的荷电状态(state of charge,SOC)和剩余寿命(remaining useful life,RUL)。数据分析的算法选择也将影响结果的精度和处理时间的长短。
1 荷电状态估算
荷电状态是指在一定的放电倍率条件下电池的剩余电量与相同条件下额定容量的比值[2]。荷电状态估算主要有如下几种方法。
1.1 电流积分法
电流积分法是对电流进行积分得到充入电池和从电池释放出的电量。该方法需对电池的电量进行长时间的记录和监测。电流积分法的优点是算法简单,易于实现,能给出任意时刻电池的电量。但是电流测量的精度将直接影响剩余电量估算结果,需要通过大量实验来建立电池充放电效率经验公式,因此该方法一般不适用于电池SOC的动态估算。
1.2 开路电压法
电池的开路电压与电池电动势在数值上近似相等,电池电动势与SOC之间存在固定的函数关系,一旦能获得足够的不同温度下SOC和开路电压(open circuit voltage,OCV)的对应关系,则从OCV推理到SOC就会变得非常直接。由此出现了一种基于电流曲线斜率和SOC关系的估算方法,将其作为常规SOC-OCV表的补充以确保其准确性和有效性。通过实验确定它们间的关系,然后通过测量电池的开路电压来估算SOC。开路电压法比较简单,估算的SOC值也较准确,缺点是不能动态估算电池的SOC。电池工作结束后必须进行长时间的静置,以使电池恢复到稳定状态,用稳定的开路电压才能估算出准确的SOC。该方法只是用于电池非工作状态下的预测。这种基于数据表的估算方法很难在现实中找到与之匹配的外界条件,由此导致了SOC估计值和真实值间存在巨大差异[2]。
1.3 内阻法
该方法通过计算电池的内阻并建立计算模型来推算SOC。电池内阻可分为交流内阻和直流内阻,它们都与SOC值存在密切的关系。该方法只能反映电池在某特定放电条件下的SOC值,如要判断电池能继续释放的电量还必须考虑以后阶段的放电倍率、温度等。该方法在电池的放电后期有较高的精度和适应性,但内阻的计算需要考虑端电压、放电倍率等诸多因素的影响,特别是在电动车实际运行工况下,当电流变化较快时计算起来比较困难,且与电池SOC的关系不容易确立,因此,该方法很少应用于电池荷电状态估算。
1.4 模糊推理
基于电化学阻抗谱通过建立锂离子电池模糊推理模型估算SOC的方法精确度很高,误差幅度仅为其他方法的10%,且只需少量的电化学参数就可加速阻抗谱测试和减少数据收集过程中的冗余,但是庞大的实验设备和高花费限制了该方法的实际应用范围。
1.5 自回归滑动平均数模型
自回归滑动平均数(autoregressive moving average,ARMA)模型[1]是一种非常适合时间序列的预测算法,表示为

式(1)中:χ是时间序列;α是常量;ε是白噪声;p指AR(自回归参数);q指MA(滑动平均参数);t和i均为整数,且t大于i;φ和θ是模型的系数。
将电解质电阻、电荷转移阻值和层间电容输入到ARMA模型,就可以通过阻抗测量来估算SOC。ARMA模型的精确性依赖于先验数据的完整性和典型性。在现实应用中,原始数据很有可能是不完整的,因此需要用回归模型来做合理估计和逐步推测。
1.6 电化学阻抗谱
电化学阻抗谱(electrochemical impedance spectroscopy,EIS)被广泛应用于表达化学电池的内部电化学反应。当电池的容性阻抗和感性阻抗相等时,在一定频率范围内SOC和EIS之间有确定的关系,而且该频率范围是电池SOC单调周期性函数。因此,可以通过选择想要的频率范围来确定电池的SOC值[3]。该方法直观、可靠性高,但阻抗谱分析仪价格昂贵,要求实验过程中外界条件保持恒定。
1.7 支持向量机
支持向量机(support vector machine,SVM)通过数据映射将低维空间的非线性问题转化为高维空间的线性问题。Hansen和Wang[4]使用SVM建立了一个基于实验的SOC估算模型,输入向量包括电流、电压,在上次计算结果和电压变化的基础上递推出当前SOC。该SOC估算模型只使用稳态数据进行训练,测得的稳态SOC和动态SOC估算均方根误差分别为5%和5.76%。SVM衰减模型需要对实验参数和误差进行不断地调整,而这是一个非常耗时的过程。
1.8 基于支持向量机的扩展卡尔曼滤波
扩展卡尔曼滤波(extended kalmanfllter,EKF)通过使用偏导数和泰勒级数展开式使预测和更新部分的当前估计值线性化,剩下的过程类似于传统卡尔曼滤波。受限于泰勒级数在高阶非线性系统中的误差,EKF不能处理高阶非线性系统问题。为了提高动态SOC估算的准确性,Lee[2]提出了一个基于物理学的“增强型自我修正模型(enhanced self-correcting model,ESC),其电压估算方程为:
Vk=OCV(SOCk,Cn,k)- Vd,k- Ri·ik(2)式(2)中:Vk是待测电压;k是标识数;Cn,k是电容;Ri是电阻;ik是电流;Vd,k是容抗导致的压降;SOCk是电池荷电状态。
该模型强调了应对滞后、温度和松弛带来的影响。容量估算的准确性在很大程度上依赖于初始值的选定,而不适当的初始化将会导致估计值和真值间明显的收敛滞后。
根据锂离子电池所处环境,预设一组Q0进行预测递推。根据这n组过程噪声值计算出实时过程噪声方差阵。设在EKF滤波的第k步时计算出的过程噪声方差阵为,在EKF滤波的第(k+1)步时要用到的过程噪声方差矩阵为Qk,则Qk和之间存在线性关系。Qk即为下次EKF滤波时要用到的过程噪声方差阵,这样就得到了一个较为准确的Qk+1阵,实现了过程噪声方差阵的实时更新,从而能更准确地估算SOC。
表1为上述方法的比较。
2 剩余寿命预测
锂离子电池剩余寿命是指满容量电池从开始放电到输出电压下降至终止电压的时间。剩余寿命预测使得在电池永久损坏前有足够的时间来采取适当的措施预防事故的发生。此外,准确的剩余寿命预测还能促进新服务模式的发展,如“智能电池流动服务系统”。锂离子电池剩余寿命预测应充分考虑当前电池的健康状态、历史数据、故障机理和故障传递等因素。尽管现在剩余寿命预测还不是文献研究中的热点,但是关于这方面的研究正不断深入。

表1 荷电状态估算方法比较
2.1 Rakhmatov 模型[6]
如果把电化学反应中活性物质的运动抽象为有限区域上的一维扩散问题,则根据法拉第定律和菲克定律,就能推导出负载电流i(τ)和电池寿命L的关系式:
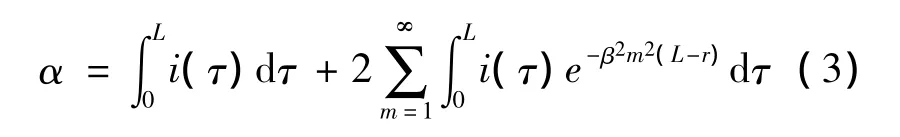
式(3)中:α的物理意义是电池可以输出的最大容量;β表示在电极表面活动载流子被补偿的速率,它可以用来衡量电池放电特性,β越大,电池放电特性越好。
对于常数负载,设电流i(t)=I,把它代入式(3),如果 β2L≥1,则可近似得到
对于变化负载,设U(t)为阶梯函数,则[0,t]时间内的可变i(t)可以用N步阶梯函数来近似,表达式为

其中,Ik是[tk,tk+1]时间内的平均负载。
该模型能精确地预测电池的剩余寿命,但需要大量的指数运算。
2.2 粒子滤波
粒子滤波(particle filter,PF)是一种序列蒙特卡罗方法,通过粒子及其权重系数来估算概率分布函数(probability distribution function,PDF)的状态。粒子的递推分2阶段:预测阶段和更新阶段。在预测阶段,下一步粒子值是通过前一步的信息来估算的,而与测量和观察无关;在更新阶段,将预测阶段通过估算得到的粒子值与测量结果进行比较并做相应更新。
Saha[7]运用粒子滤波来估算电解液阻抗和电荷转移阻抗指数增长模型的系数,建立了电解液阻抗、电荷转移阻抗和容量之间的函数关系,根据估算的电解液阻抗和电荷转移阻抗来推断电池未来容量,最终计算出剩余寿命。阻抗测量的高费用和严格的外界约束条件参数限制了这种方法的实际应用。在不测量电化学阻抗谱的条件下,Saha和Goebel[8]建立了一个考虑库伦效能因素和松弛作用的容量实验模型。该方法采用粒子滤波来估算电池模型的不同组成部分,进而推算电池的剩余寿命。
2.3 关联向量机
Saha[9]提出了一种基于电化学模型的电池内部参数的关联向量机(relevance vector machine,RVM)衰减模型,用来准确跟踪退化趋势,并采用粒子滤波算法选择合适的RVM模型系数,进而预测剩余寿命终结点。
当关联向量机的输入为任意分布的随机变量时,关联向量机的输出为

式(6)中:p(y*)为随机变量y*的分布密度函数;
关联向量机不仅能够反映输出结果的不确定信息,并且拥有学习算法简单、易实现等优点。
上述3种预测剩余寿命的方法中,Rakhmatov模型尽管能很好地仿真电池负载电流与剩余寿命之间的关系,但是指数运算过于复杂,处理时间较长;粒子滤波方法可以估算电池各部分间的复杂变化关系,进而能精确地预测剩余寿命;而关联向量机所采用的模型系数也需通过粒子滤波算法估算。p(x*)为随机变量x*的分布密度函数;x*∈Rq;q为随机变量x*的维数;p(y*|x*)为关联向量机模型在输入为x*时的输出结果分布。
一般情况下,上述积分是无法以解析形式求解的。若对输入随机变量x*采样N个独立同分布的样本粒子xi*,则上述积分结果可以表示为

式(7)中:p(y*|xi*)为关联向量机模型在输入为确定值xi*时的输出结果的分布,具有高斯分布形式,并且由其均值和方差唯一确定。式(7)表明:当关联向量机回归模型的输入为一任意分布的随机变量时,其预测输出的分布可以由一组高斯分布随机变量的加权和形式给出。
3 结束语
锂离子电池被广泛应用于各个领域,其生产制造技术正不断得到发展,可靠性也在逐步得到改善。但是不论多么好的锂离子电池,都会随着时间退化,并且退化速率受外界环境和操作规程的影响。在现有的实验条件下,除了提高检测设备精度外,选择合适的算法对于不同技术要求的锂离子电池至关重要。尤其是对于电池使用者而言,在检测设备便携的情况下,算法越简单、处理时间越短、结果越精确,越受用户欢迎。其中,粒子滤波算法摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约条件,并且在预测方面精度很高,相信在锂离子电池健康预测方面,该算法的应用范围会更加广泛。
[1]Zhang Jingliang,Lee Jay.A review on prognostics and health monitoring of Li-ion battery[J].Journal of Power Sources,2011,173(2):426-432.
[2]Lee S,Kim J,Lee J.The state and parameter estimation of an Li-ion battery using a new OCV-SOC concept[C]//IEEE Power Electronics Specialists Conference,2007.PESC 2007.2007:2799-2803.
[3]Blanke H,Bohlen O,Buller S.Impedance measurements on lead-acid batteries for SOC,SOH and cranking capability prognosis in electric and hybrid vehicles[J].Journal of Power Sources,2005,144(2):418-425.
[4]Hansen T,Wang C J.Support vector based battery state of charge estimator[J].Journal of Power Sources,2005,141(2):351-358.
[5]Puglia F,Cohen S,Hall J,et al.Very Large Lithium Ion Cell and Battery Designs,Anonymous[C]//AABC-05.2005.
[6]Daler R.A model for battery lifetime analysis for organizing applications on a pocket computer[J].IEEE Trans On VLSl Syaem,2003,11(6):1019-1030.
[7]Saha B,Poll S,Goebel K.An Integrated Approach to Battery HealthMonitoring using Bayesian Regression and State Estimation[C]//Autotestcon,2007 IEEE.2007:646-653.
[8]Saha B,Goebel K.Modeling Li-Ion Battery Capacity Depletion in a Particle Filtering Framework.2009.

