具有庇护所的Kolmogorov型捕食-食饵系统的研究

林 琳，雒志学

(1.运城农业职业技术学院基础教学部，山西运城 044000;2.兰州交通大学，兰州 730070)

近年来，许多学者对食饵具有庇护所效应的捕食系统开展了研究，且获得了很好的结果［1-8］，但对于Kolmogorov模型的研究成果还不多见。本文以Kolmogorov模型［9］为基础，建立了一类具有庇护所效应的两种群捕食-被捕食模型。

1 模型假设及建立

假定捕食者和食饵种群的密度随时间连续变化，并且均匀分布于生境斑块上。两种群均被视为同质种群，即无阶段结构。基于以上假设，建立了Kolmogorov型捕食-食饵系统:

其中，x(t)和y(t)分别表示食饵种群和捕食者种群在t时刻的密度。模型(1)基于以下假设:①存在正常数 K，使得对于一切的 0＜x＜K，均有g(x)＞0;g(K)＞0;②对于一切的x≥0，有φ(0)=0，φ'(x)＞0;③ 函数 g(x)和 φ(x)是 (0 ，+ ∞ )的连续可微函数。

如果假设食饵种群的增长率满足Logistic定理，捕食者具有Holling型的饱和功能反应，那么系统(1)变为:

其中:r为食饵种群的内禀增长率;K是环境容纳量;q表示捕食者的最大消耗率;p表示从食饵转化为捕食者增长的转化率;c为捕食者的死亡率。r、K、q、a、p、c均为正常数。

用xR表示庇护所中的食饵密度，那么将庇护所效应引入系统(2)，则得到具有庇护所效应的捕食-食饵系统:

其中假定c＜p＜2c。

本文从2个方面来讨论庇护所效应:①庇护所中的食饵密度与现有密度成正比，比例常数为γ，即xR=γx，(0≤γ≤1);② 庇护所中的食饵密度为常数，即xR=R。本文只分析第1种情形，第2种情形的讨论与第1种情形类似。

2 主要结果

如果庇护所中的食饵密度与现有密度成正比，比例常数为γ(0≤γ＜1)，则系统(3)变为

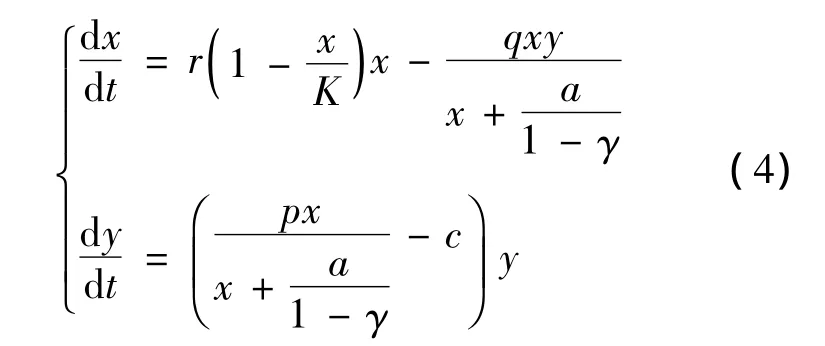
P(x*，y*)退化为平衡点 PK(K，0)。令 x(o)=，其中下标(n)表示新的变量，下标(o)表示旧的标量，则系统(4)变为

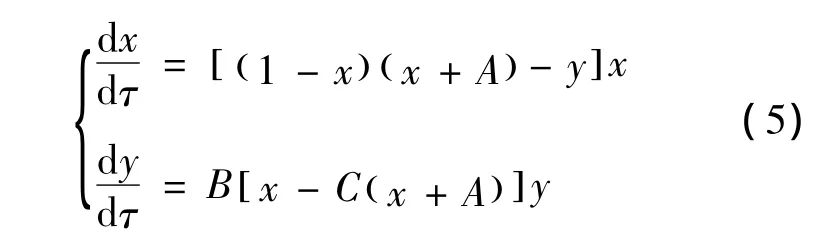
其中:A=(a'/K);B=(p/r)＜1;C=(c/p)＜1。

如果1-C-AC=0，则平衡点Q(x*，y*)退化为Q1(1，0);如果1-C-AC＜0，则平衡点Q(，)位于第4象限，这时系统(5)只有2个非负平衡点:O(0，0)、Q1(1，0)。

下面给出关于平衡点稳定性的结论。

定理1

1)原点O(0，0)为系统(5)的鞍点。

2)若1-C-AC ＞0，平衡点 Q1(1，0)为系统(5)的鞍点;若1-C-AC ＜0，平衡点 Q1(1，0)为系统(5)的稳定焦点或结点。

证明

1)系统(5)在原点O(0，0)处的Jacobia矩阵为显然矩阵有一正一负的特征根:λ1=A，λ2=-ABC，所以初始平衡点O(0，0)为不稳定鞍点。

2)系统(5)在平衡点Q1(1，0)处的Jacobia矩阵为个特征值分别为:λ1=-1-A，λ2=B(1-C-AC)。显然，当1-C-AC＞0时，平衡点 Q1(1，0)为系统(5)的鞍点;当1-C-AC＜0时，平衡点Q1(1，0)为系统(5)的稳定焦点或结点。

定理2 当1-C-AC＜0时，系统(5)从R2+中任一点p(xp，yp)出发的解有界。

证明 作直线 x=l1，l1≥max{xp，1}，则当 y ＞0时，故当系统(5)的轨线与直线x=l1相遇时，均从直线x=l1的右方穿入左方。作直线y=l2，l2≥0，则当0＜-AC)＜0。故当系统(5)的轨线与直线y=l2相遇时，均从直线y=l2的上方穿入左方。

由于x=0，y=0都是系统的轨线，于是由直线 x=0，y=0，x=l1y=l2可围成区域 D，系统(5)从中任一点p(xp，yp)出发的解只能在该区域内，所以有界。定理2成立。

［1］林琳，侯林洁.具有庇护所的Lotka-Volterra型的捕食-食饵系统［J］.北华大学学报:自然科学版，2012(13)1:19-21.

［2］帅智圣，苗春梅，张伟鹏，等.具有庇护所的三种群捕食者-食饵模型［J］.生物数学学报，2004，16(1):65-71.

［3］张艳波，王万雄，段永红.一类具第三类功能反应且食饵具有避难所的捕食系统的分析［J］.数学的实践与认识，2010(40):149-154.

［4］徐国明，贾建文.一类具有避难所的不是系统的分析［J］.陕西师范大学学报，2007，21(4):4-7.

［5］周稻祥，朱长荣.一类具有常数避难所与收获率的捕食-食饵模型的稳定性分析［J］.重庆理工大学学报:自然科学版，2012，26(12):122-126.

［6］徐昌进，陈大学.具有时滞的食饵-捕食者模型的分支问题［J］.重庆师范大学学报:自然科学版，2011(3):43-48.

［7］帅智圣，苗春梅，张伟鹏，等.具有庇护所的三种群捕食者-食饵模型［J］.生物数学学报，2004，28(1):65-71.

［8］马智慧，李文龙，李自珍，等.具有已感染者庇护所效应的传染病模型［J］.兰州大学学报，2008，44(2):111-114.

［9］陈兰荪.数学生态学模型与研究方法［M］.北京:科学出版社，1988.

［10］马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京:科学出版社，2001.