基于隐马尔可夫模型的双链马尔可夫模型
陈 琦,吾拉木江·艾则孜,申建新,胡锡健
(新疆大学数学与系统科学学院,乌鲁木齐 830046)
隐马尔可夫模型(HMM)作为一种统计分析模型,最初是在20世纪60年代后半期由Leonard E.Baum和其他一些作者提出的,经过近半个世纪的发展,现已成功应用到语音识别、生物信息科学、故障诊断等领域。HMM要求模型的输出之间是条件独立的,然而这种假设在实际应用中有时并不合理。A.Berchtold[1]提出了双链马尔可夫模型(DCMM)。DCMM可以看成是对HMM的扩展,其模型的输出之间具有直接关系。DCMM虽然已提出10多年,但国内学者对其研究很少。本文对DCMM的概念、发展及其基本问题进行介绍,并利用其与HMM之间的区别,通过本文所提出的推导条件,从与HMM基本问题有关的一套概念及算法推导出DCMM的一套概念及算法。
1 隐马尔可夫模型
1.1 HMM符号化
定义 {Ut:t=1,2,…,T}是观察序列;{St:t=1,2,…,T}是隐状态序列。用(t)和(t)分别表示{Ut,1≤t≤t}和{St,1≤t≤t},那么,可以通过以下2个公式来描述一个隐马尔可夫模型[2]:

也可以将一个离散HMM用一个5元组表示:λ =(M,N,π,A,B),其中:M 表示隐状态的数目;N表示可观测状态数目;π表示初始状态的概率分布,π ={πi},πi=P(S1=i),1≤i≤M;A 表示隐状态转移概率矩阵 A={ai,j},ai,j=P{St+1=j|St=i},1≤i,j≤M;B表示给定状态下的观察概率分布,B={bjk},bjk=bj(k)=p(Ut=k|St=j),1≤k≤N,1≤j≤M。还可以将上述5元组简写成一个3元组:λ=(π,A,B)。由于此马尔可夫链有M个隐状态,因此可称其为一个M状态马尔可夫模型。注意,本文所讨论的是离散HMM,连续的情况可以类似推出。
1.2 与HMM问题有关的概念及算法
1.2.1 观察序列的联合概率[2]
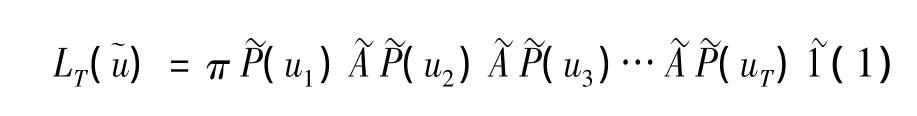
1.2.2 向前向后概率[3]
对 t=1,2,…,T,定义如下行向量:

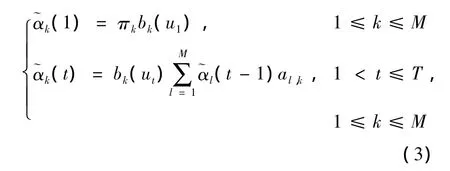
同样可以定义向后概率向量:
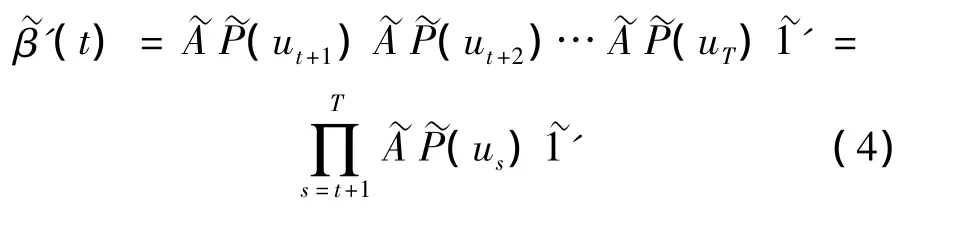

由向前概率与向后概率的定义可以得到

1.2.3 Lk(t)和 Hk,l(t)的定义[3]
在一组给定的参数集下,定义:

不加证明地给出以下结论:
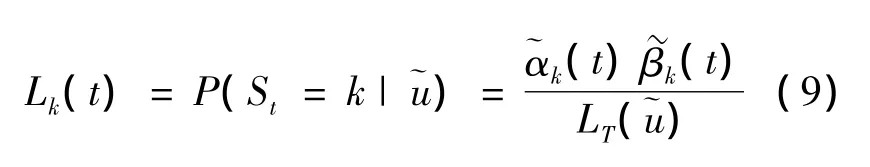

1.2.4 HMM学习问题的EM算法[4]
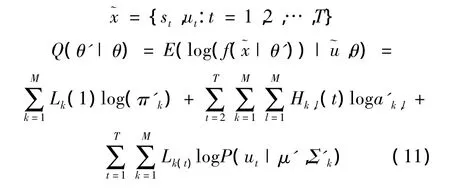
EM算法步骤如下:
3)用计算得到的 Lk(t)、Hk,l(t)更新参数:
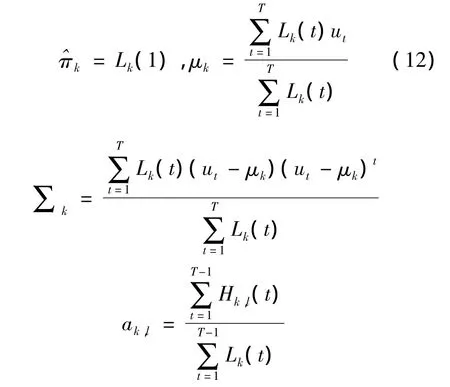
1.2.5 HMM解码问题的Viterbi算法[5]
定义 δt(i)=maxP(s1,s2,…,st-1,st=i,u1,u2,…,ut|λ),即求 T 时刻最大的 δT(i)所代表的状态序列。
算法步骤:
1)初始化:δ1(i)= πibi(u1),φ1(i)=0,1≤i≤M;
2)递归:δt(j)=max[δt-1(i)ai,j]bj(ui),2≤
2 双链马尔可夫模型
2.1 模型简介
DCMM是一个未知(隐)模型和一个已知(明)模型的特性的某种组合,之所以称其为双链,是因为它可以被看作2个马尔可夫链的叠加。其中的隐链控制一个未观察到的变量的状态之间的关系,明链控制一个观察到的变量的输出之间的关系。DCMM是为非齐次时间序列建模而设计的。Berchtold[6]提出:如果一个时间序列可被分解成一个有限的转移矩阵的集合,那么DCMM可以用来控制这些矩阵的转移过程。模型的结构可以用图1描述。
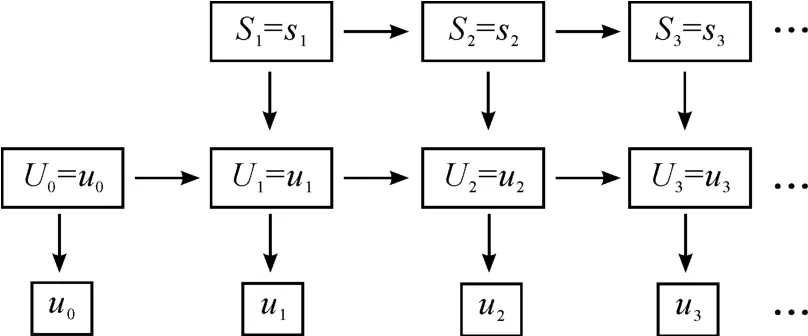
图1 双链马尔可夫模型结构
可以看到:DCMM使一个HMM的输出之间具有了某种关系,而一个HMM的输出之间不存在任何关系。之前也有一些学者按照类似的想法(使一个HMM的输出之间具有某种关系),提出过一些模型。Poritz、Kenny[7-9]提出一种将 HMM 与自回归模型结合的方法,Wellekens和 Paliwal[10-11]先后提出了一种类似的DCMM模型,前者针对连续HMM情况,后者针对离散HMM情况。
2.2 模型符号化
本文研究的是输出为离散的情况。一个双链隐马尔可夫模型包含2个随机变量:St和Ut。St,Ut表示含义和HMM模型相同,即St表示隐状态,Ut表示观察序列。那么一个DCMM模型可以用一个3 元组表示:κ(π,A,C)[1]。
一个隐状态的集合为G(S)={1,…,M},一个可能输出的集合为G(U)={1,…,N},隐状态的初始分布为π ={πi},πi=P(S1=i),1≤i≤M,隐状态间的转移概率矩阵为A={ai,j},ai,j=P{St+1=j|St=i},1≤i,j≤M。给定隐状态 St时连续输出ut之间的转移矩阵集合用C={C(k)}表示,其中C(k)=)i,j∈G(U),k∈G(S)。
一个DCMM是马尔可夫链和HMM的结合。当只有一个隐状态(M=1)时,DCMM变成一个转移矩阵为C(1)的齐次马尔可夫链;当隐状态数M>1时,每个矩阵C(k)有相同的行,DCMM变成一个HMM。
2.3 DCMM的基本问题
1)模型给定时观察序列u0,u1,…,uT的似然函数的估计。
2)给定观察序列 u0,u1,…,uT时模型参数π、A、C 的估计。
3)在给定模型和一个输出序列的情况下隐状态序列的最优估计。
3 HMM到DCMM的推导
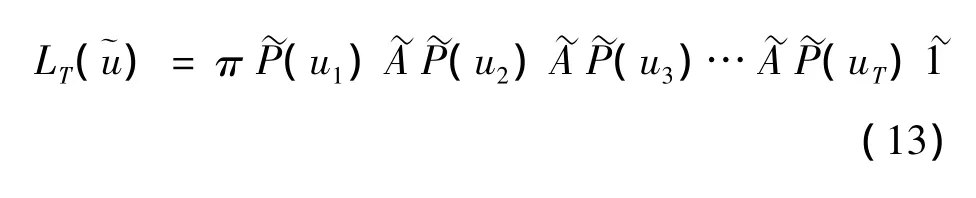
在DCMM中向前、向后概率及Lk(t)、Hk,l(t)与在HMM中定义一样,只做如下变换(t)中:
由HMM导出DCMM学习问题的EM算法,前两步同HMM学习问题的EM算法,只需将第3步中的利用条件变为
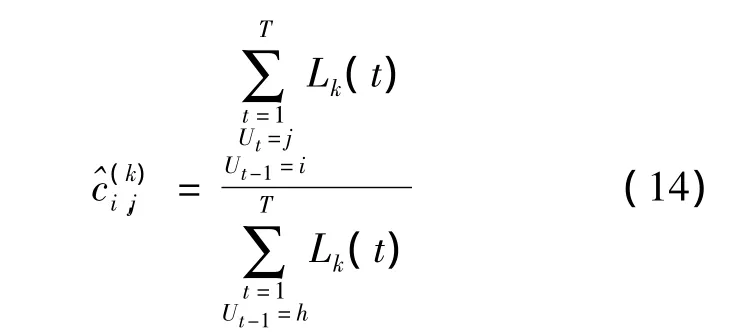
由HMM导出的DCMM解码问题的Viterbi算法:定义 δt(i)=maxP(s1,s2,…,st-1,st=i,u1,u2,…,ut|κ),即求T时刻最大的δT(i)所代表的状态序列。在解决HMM问题的Viterbi算法中做以下变换可得 解 决DCMM解码问题的Viterbi算法。
根据文献[1],上述推导结果所得结论与文[1]中的结果相同,从而简化了DCMM模型的参数估计算法推导过程。即经过适当的变化,可以将HMM的一套估计算法理论用到DCMM模型中。观察序列u0,u1,…,uT的似然函数的估计,可以利用式(13)及DCMM向前概率、向后概率得到。给定观察序列u0,u1,…,uT时,模型参数 π、A、C的估计问题可以利用EM算法解决。在给定模型和一个输出序列的情况下,隐状态序列的最优估计问题可以利用Viterbi算法解决。
4 推导条件分析
5 结束语
本文分别对HMM及DCMM进行了介绍,发现并利用2种模型之间的关系,提出了从HMM到DCMM的推导条件,从而由HMM一套估计算法推导出了DCMM的一套估计算法,并分析验证了这种推导的可行性,从而完成了基于比较熟悉的HMM到不太熟悉的DCMM的研究,为算法创新提供了新的思路。
[1]Berchtold A.The Double Chain Markov Model[J].Communications in Statistics-Theory and Methods,1999,28(11):1-8.
[2]Zucchini R W,Donald I M.Hidden Markov Models for Time Series An Introduction Using in R[M].Boca RatonFL:Chapman & Hall/CRC,2009.
[3]Li J.Hidden Markov Model-Penn State Department of Statistics[EB/OL].[2002-08-22].sites.stat.psu.edu/~jiali/course/stat597e/notes2/hmm.pdf.
[4]Olivier Cappé,Eric Moulines,Tobias Rydén.Inference in Hidden Markov Models[M].New York:Springer,2005.
[5]Forney G D.The Viterbi Algorithm[J].Proceedings of the IEEE,1973,61:268-278.
[6]Berchtold A.Learning in Markov Chains[C]//Apprentissage,des principes naturels aux methodes artificielles.Ritschard,Berchtold.Paris:HERMEZ,1998.
[7]Poritz A B.Linear predictive hidden Markov models and the speech signal[J].Proceedings ICASSP,1982:1291-1294.
[8]Poritz A B.Hidden Markov models:A guided tour[J].Proceedings ICASSP,1998,1:7-13.
[9]Kemeny P,Lennig M,Mermelstein P.A linear predictive HMM for vectorvalued observations with applications to speech recognition[J].IEEE Transactions on Accoustics,Speech,and Signal Processing,1990,38(2):220-225.
[10]Wellekens C J.Explicit time correlation in Hidden Markov Models for speech recognition[J].Proceedings ICASSP,1987:384-486.
[11]Paliwal K K.Use of temporal correlation between successive frames in a hidden Markov model based speech recognizer[J].Proceedings ICASSP,1993,2:215-218.

