汽车前驱变速器试验台阶跃响应特性分析
石晓辉,汤 亮,邹喜红,钱晓渝,易 鹏
(1.重庆理工大学,重庆 400054;2.重庆铁马工业集团有限公司军品技术研究所,重庆 400050;3.重庆市科学技术研究院,重庆 401123)
随着变速器试验技术的发展,变速器室内台架模拟试验已成为变速器设计开发过程中最主要的试验手段。为尽可能完全地在试验台上模拟真实的行驶工况和行驶载荷,需要对变速器试验台动态特性提出更高的要求。目前,国内研究主要集中在试验台静态和准静态研究方面,而对试验台动态特性方面的研究很少[1-4]。变速器试验台阶跃响应特性可以直接反映试验台动态特性的好坏,因此本文针对典型的三电机试验台建立了动力学模型,以阶跃信号为输入分析了其阶跃响应特性,为高动态特性变速器试验台的设计和优化提供了重要的分析手段和方法。
1 结构
本前驱变速器试验台采用三电机试验方案,基本结构如图1所示。试验台由变频控制系统、驱动电机、加载电机、膜片联轴器、扭矩转速传感器、被测变速箱等组成。由于本试验台为前驱变速器试验台,因此需在被测变速器两侧半轴处分别连接1个加载电机,模拟变速器负载。
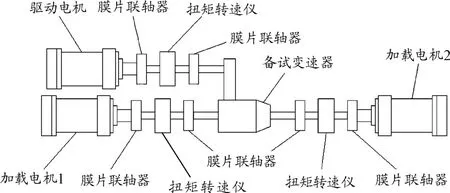
图1 试验台基本结构
2 试验台模型
前驱变速器试验台由驱动端和加载端及被测变速器3部分构成。驱动端由驱动电机通过联轴器经半轴与变速器输入端相连,加载端则分别与变速器两侧输出轴连接。为了保证模型的完整,同时也为了便于调整参数,采用模块化的建模思路,分别对试验台驱动端、加载端2个单元进行建模[5]。
2.1 前驱变速器试验台驱动单元模型
汽车前驱变速器试验台驱动单元由驱动电机、膜片联轴器、扭矩转速传感器及被测变速器构成,其基本组成和力学模型分别如图2、3所示。

图2 驱动单元组成
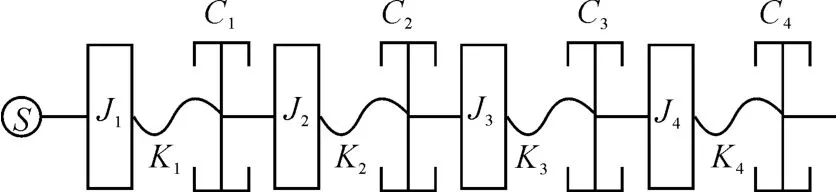
图3 驱动单元力学模型
如图3所示,对每个部件进行动力学建模。由于该系统为多阻尼、多刚度系统,其动力传递表现为非线性,不利于系统的建模,因而忽略弹性联轴器输出轴、扭矩转速仪、弹性联轴器输入轴转动惯量,并引入等效刚度和等效阻尼的概念。驱动单元简化力学模型如图4所示。
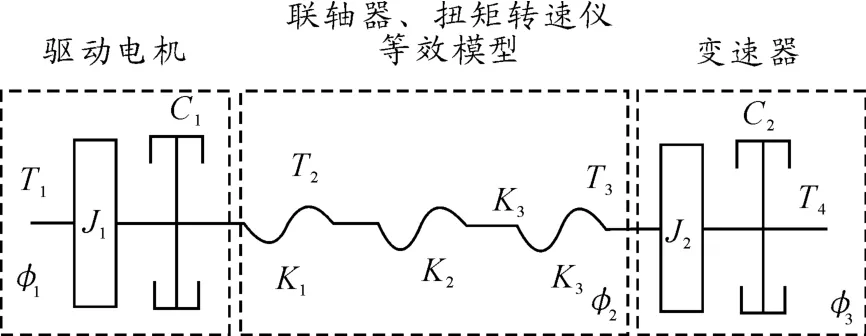
图4 驱动单元简化力学模型
驱动端力矩平衡方程如下:

经拉普拉斯变换可得传递函数:


式中:T1为驱动电机理论输出转矩;T2为联轴器输入轴转矩;C1为驱动电机等效阻尼系数;C2为联轴器阻尼系数;J1为驱动电机转动件、输出轴及膜片联轴器输入轴等效转动惯量;φ为驱动电机输出轴转角;φ1、φ2为联轴器输入轴、输出轴转角;J2为驱动电机转动件、输出轴及膜片联轴器输入轴等效转动惯量;T3为联轴器输出端转矩。
2.2 前驱变速器试验台加载单元模型
试验台加载单元的构成与驱动单元基本相同,其基本组成如图5所示。与驱动端同理,为方便建模,对加载端稍作简化,忽略弹性联轴器的输出轴、扭矩转速仪、弹性联轴器的输入轴等效传动惯量,可得加载端简化力学模型,见图6。
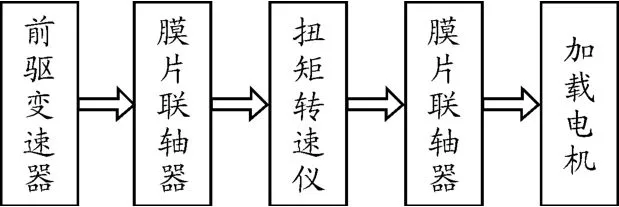
图5 加载单元组成
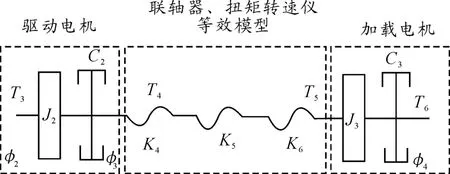
图6 加载单元简化力学模型
由于加载端力矩平衡方程推导过程与驱动端相似,因此不再赘述,其传递函数如下:

式中:T3为变速器输入端转矩;T4为联轴器输入轴转矩;C2为变速器阻尼系数;C3为加载电机阻尼系数;T5为联轴器输出轴转矩;J2为驱动电机转动件、输出轴及联轴器输入轴等效转动惯量;φ为变速器输入端转角;φ1、φ2为联轴器输入轴、输出轴转角;T5为联轴器输出轴转矩。
3 仿真分析
3.1 试验台基本参数及评价指标
将前驱变速器试验台驱动单元、加载单元拼接成试验台整体模型,并运用Matlab建立Simulink 模型,如图7 所示[6]。
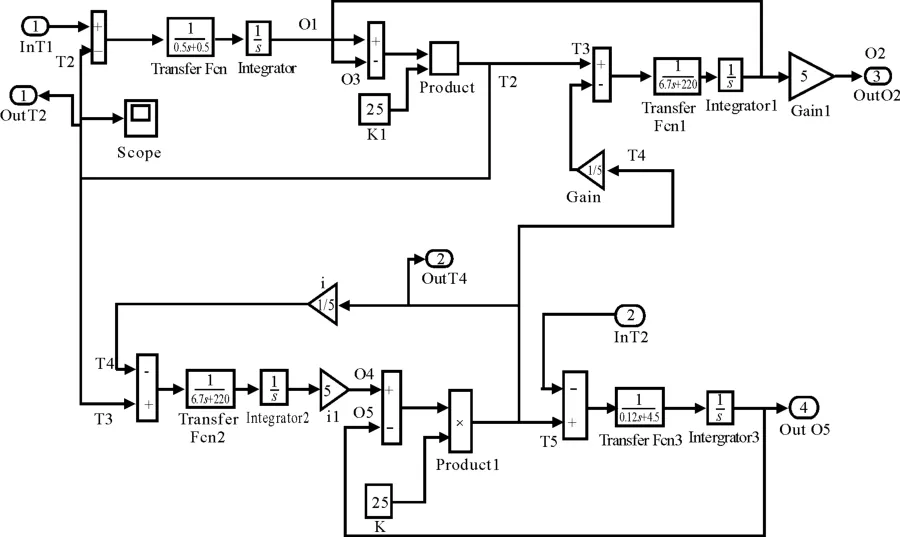
图7 试验台Simulink模型
根据所建试验台模型,分析在阶跃输入下系统的动态响应特性,运用控制变量法分析同一参数不同数值对系统转矩及转速响应特性的影响。根据 A.R.Crowther在《Design and Analysis of a Gear Rattle Test Rig》中的经验数据[7],初步确定试验台参数选型方案。选取的试验台基本系统参数如表1所示。
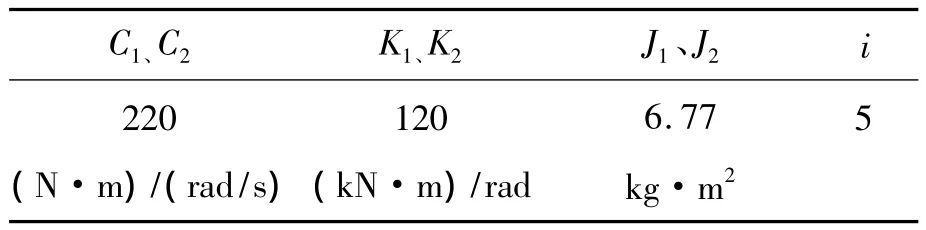
表1 试验台基本系统参数
由试验台模型可得在不同惯量J、刚度K、阻尼C的情况下变速器输入端转矩、转速响应曲线以及驱动端转矩转速响应曲线。在控制理论、数理统计与数值分析的基础上,借鉴动态响应特性评价性指标[8],提出了阶跃响应特性评价指标(见表2),对仿真结果进行比较与分析。鉴于试验台整体为封闭系统,任一部件参数变化都能影响试验台的阶跃响应特性,本文选取驱动电机惯量、驱动电机阻尼以及驱动端等效刚度K1进行研究。

表2 转矩响应特性评价指标
3.2 不同试验台机械参数对阶跃响应特性的影响分析
在所建立模型和初定参数基础上,针对每一种力学参数,根据初定参数另外选择两组力学参数与其进行分析对比。
图8、9分别为在不同电机转动惯量J1下于加载端突加100 N·m阶跃转矩时,系统转矩及转速的响应情况。表3为不同惯量J1下转矩响应评价参数值。
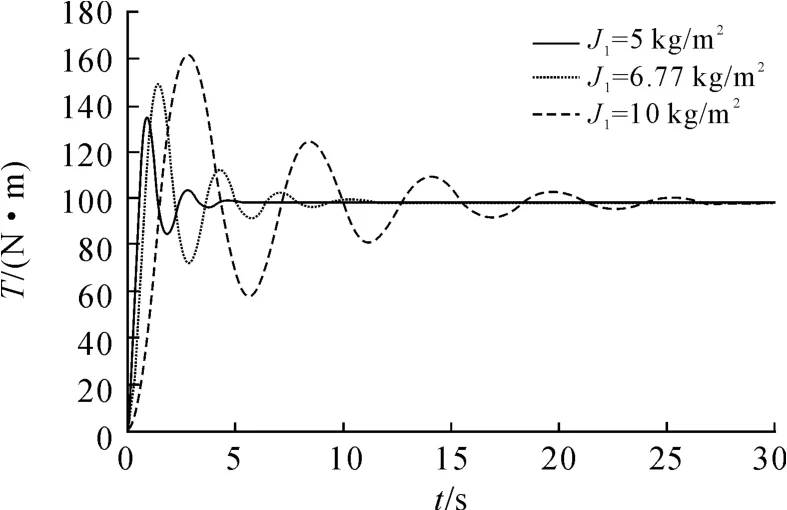
图8 不同惯量J1下转矩响应
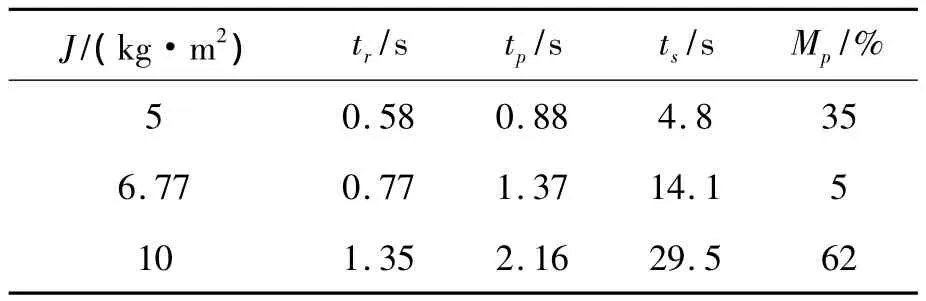
表3 不同惯量J1下转矩响应评价参数值
通过图8及表3可知:在驱动端给定100 N·m阶跃转矩信号下,系统的上升时间、峰值时间、调整时间和超调量随着J1的增大而增加。相对J1为5 kg·m2时,在J1为10 kg·m2的情况下,系统的调整时间增大了6倍,系统稳定性明显下降。这说明低惯量状态下,系统的阶跃响应特性及系统稳定性更好。
由图9及表3可知:在J1为5 kg·m2时,转速阶跃响应更快,即升速能力较强,且转速波动较小,系统更为稳定。
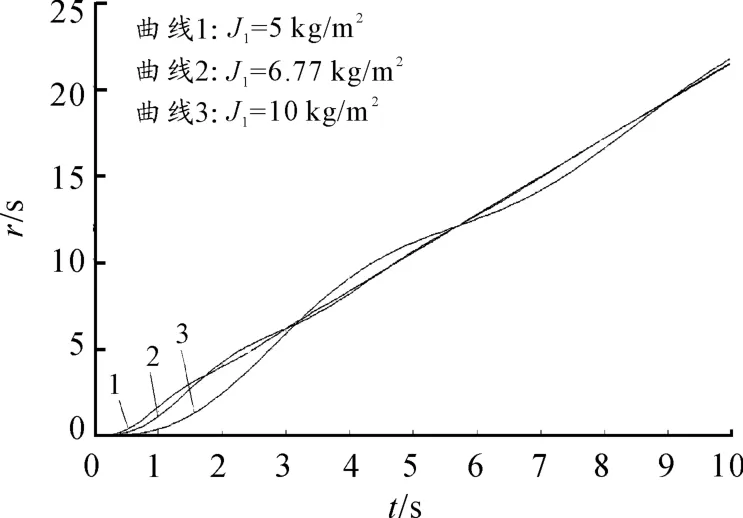
图9 不同惯量J1下转速响应
图10、11分别为在不同电机阻尼C1下于加载端突加100 N·m阶跃转矩时,系统转矩及转速的响应情况。表4为不同阻尼C1下转矩响应评价参数值。
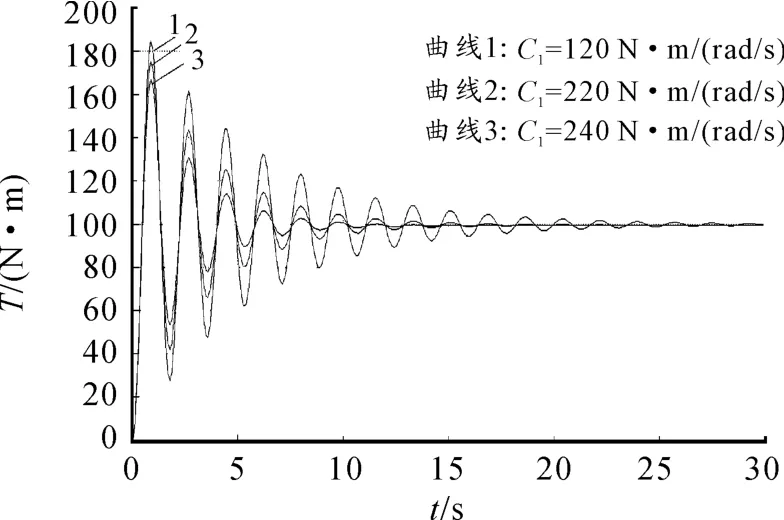
图10 不同阻尼C1下转矩响应
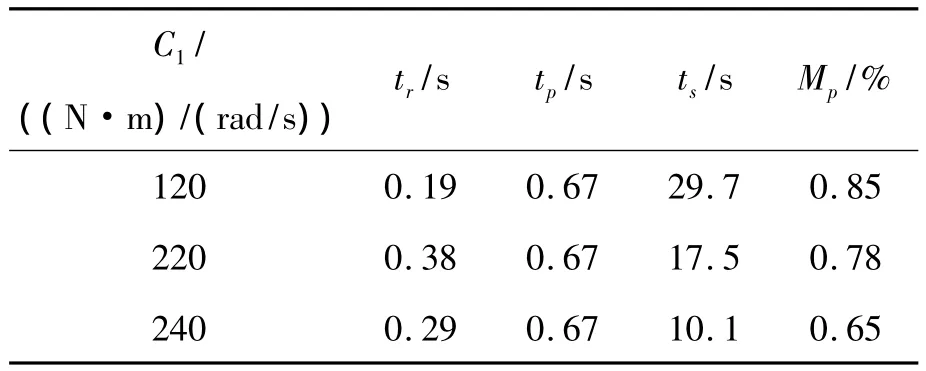
表4 不同阻尼C1下转矩响应评价参数值
通过图10及表4可知:当电机阻尼为120(N·m)/(rad/s)时,系统的升速时间较短。这说明此时系统的转矩阶跃响应特性比电机阻尼为220和240(N·m)/(rad/s)时更好。由调整时间和超调量可以看出:虽然在电机阻尼较小时系统转矩响应更快,但其转矩波动较大,振荡时间过长,不利于系统的稳定。在试验台选型过程中需综合考虑选择适当的电机阻尼。在系统稳定的前提下,实现转矩阶跃响应的最优化。
由图11可知:在不同电机阻尼下,系统的转速阶跃响应在起步阶段相同。随着转速的增加出现差别,且在低阻尼情况时,系统的升速能力略强,但同时转速波动较大。而在C1为120(N·m)/(rad/s)时,系统的升速过程更为平稳。
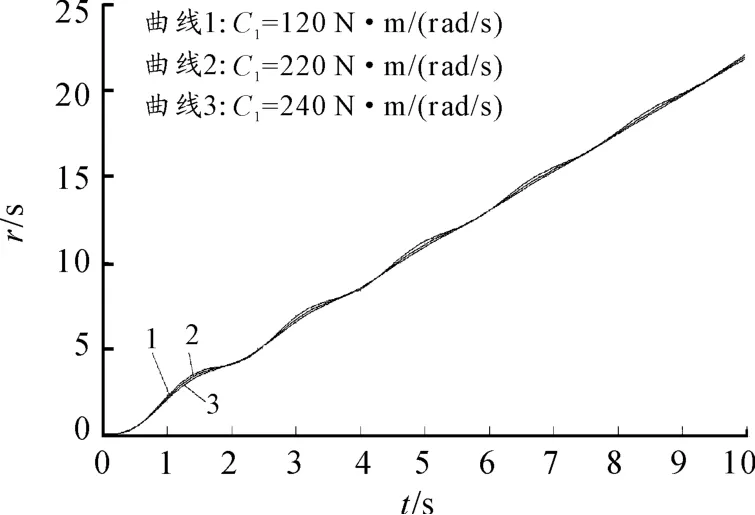
图11 不同电机阻尼C1下转速响应图
图12、13分别为在不同等效转动惯量K1下于加载端突加100 N·m阶跃转矩时,系统转矩及转速的响应情况。表5为不同惯量K1下转矩响应评价参数值。
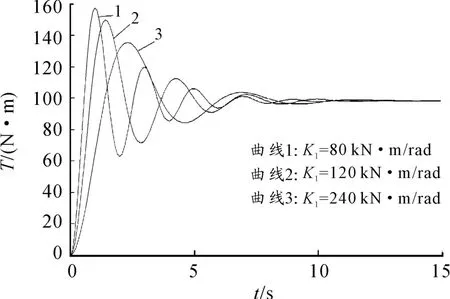
图12 不同等效刚度K1下转矩响应图
由图12及表5可知:当刚度 K1为240(kN·m)/rad时,系统的升速时间、峰值时间和调整时间较短,说明此时系统有很好的转矩阶跃响应特性。但相比刚度K1为80和120(kN·m)/rad时,刚度K1为80(kN·m)/rad时系统的超调量大,试验台易出现过载。因此,选择刚度更大的部件可以得到更好的阶跃响应特性,但考虑到试验台的形变和对中,不可能将刚度选择为最大,而应在满足设计要求的情况下,选择更利于试验台阶跃响应特性的刚度系数。

表5 不同惯量K1下转矩响应评价参数值
由图13可知:在低转速阶段,刚度K1越小,系统的升速能力越强;随着转速的增大,刚度越大,转速响应特性越优秀,且都不会出现转速波动情况。

图13 不同等效刚度K1下转速响应图
3.3 机械参数综合匹配仿真
根据前面的仿真分析,可得到在不同电机惯量J1、阻尼C1、刚度K1下的试验台阶跃响应情况。根据仿真结果,当 J1为5 kg·m2、C1为120 N·m/(rad/s)和K1为240(kN·m)/rad时,系统的阶跃响应特性更优。因此选取此组参数对机械参数综合匹配时试验台的阶跃响应特性进行仿真分析,结果如图14、15所示。
由图14、15可知:综合选取 J1为5 kg·m2、C1为120(N·m)/(rad/s)和K1为240(kN·m)/rad时,试验台的超调量为0,上升时间仅为1.7 s,且没有出现振荡和过载情况,转矩阶跃响应特性表现优秀。同时转速阶跃响应较快,且无振荡情况出现。通过综合匹配参数下试验台的阶跃响应特性分析,更进一步证明了本文提出的不同机械参数下汽车前驱变速器试验台阶跃响应特性分析评价方法的有效性。
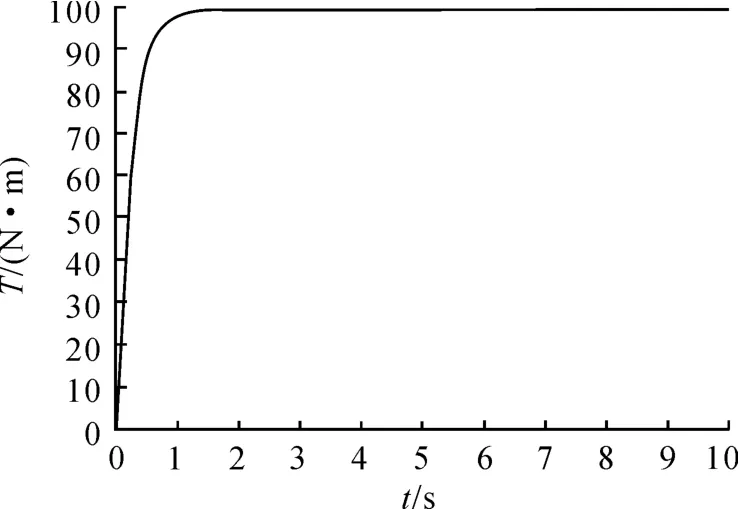
图14 综合匹配参数下转矩响应
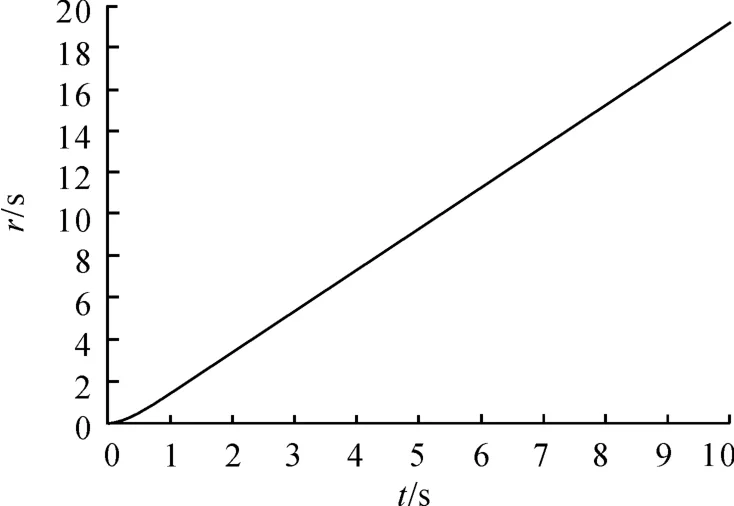
图15 综合匹配参数下转速响应
4 结论
提出了一套汽车前驱变速器试验台阶跃响应特性分析评价方法,通过研究得到以下结论:
1)惯量越低,试验台的上升时间、峰值时间、调整时间和超调量越小,转速升速能力就越强,波动、振荡就越小,响应过程更为稳定。相比初定参数,将惯量控制在5~6.77(N·m)/(rad/s)可提高试验台阶跃响应特性。
2)在试验台阻尼较小时,系统转矩响应更快,但其转矩波动较大,振荡时间过长,稳定性差。转速阶跃响应在起步阶段基本相同,但随着转速的增加,在低阻尼情况时,试验台升速能力略强,但同时转速波动较大。因此在试验台选型过程中需综合考虑选择适当阻尼。在系统稳定的前提下,电机阻尼选择在120~220(N·m)/(rad/s)对试验台动态特性更为有利。
3)刚度越大,阶跃响应特性越好,但可能出现超调量过大的情况。为使试验台具备良好的阶跃响应特性,同时避免超调量过大,将刚度控制在120~240(kN·m)/rad更为合理。
[1]宫文斌,刘安龙.机械惯量混合电模拟技术研究[J].农业机械学报,2009(1):208-212.
[2]路波.汽车传动系行驶工况模拟试验研究[D].重庆:重庆理工大学,2008.
[3]Takeshi Abe,Lawrence P.Application of Kalman Filter in Brake Inertia Dynamometer of motorcycle[J].SAE,1999(1):1837.
[4]莫志勇,吉同舟.汽车机械惯量电模拟技术[J].中国惯性技术学报,2009,17(1):123-126.
[5]张梅军,曹勤.工程机械动力学[M].北京:国防工业出版社,2012.
[6]张化光,刘鑫蕊,孙秋野,等.MATLAB/SIMULINK实用教程[M].北京:人民邮电出版,2009.
[7]Crowther A R,Rozyn M K.Design and Analysis of a Gear Rattle Test Rig[J].SAE Int J Passeng Cars,2009(1):2113.
[8]姚佩阳.自动控制原理[M].北京:清华大学出版社;北京交通大学出版社,2005.

