浅谈点关于直线成轴对称的运用

黄君明

(杭州财税会计学校,浙江杭州 310012)

浅谈点关于直线成轴对称的运用

黄君明

(杭州财税会计学校,浙江杭州 310012)

本文就点关于线成轴对称问题进行演变、挖掘,通过几何图形、距离、光线等一些问题的应用,培养学生应变、求异、探索能力,启迪学生综合运用发散思维。

对称性 图形 距离 光线

在关于直线的对称性问题的教学过程中，不仅要让学生理解和掌握基本的知识内容，能熟练地解决一些基础问题，而且要引导学生从这些基础问题为蓝本，培养学生的思维拓展、求异、探索的能力。本文就以点关于直线成轴对称为例，谈谈教学的体会。

基础问题:试求点A(1，3)关于直线L:2x-3y-6=0的对称点的坐标。

解:设A(1，3)关于L的对称点为A'(x0，y0)，则AA'的中点为M，又因M在直线L上，

所以点A(1，3)关于直线L:2x-3y-6=0的对称点的坐标为(5，-3)。

另解:设A(1，3)关于L的对称点为A'(x0，y0)，因为AA'⊥L，所以直线AA'的斜率

所以点A(1，3)关于直线L:2x-3y -6=0的对称点的坐标为(5，-3)。

这两种解题方法，虽然过程方法有所不同，但实质都基于轴对称问题的一个基础知识点，即:点A′是点A关于直线L的对称点的充要条件线段AA′⊥L且线段AA′的中点在直线L上。在教学过程，大部分学生都能理解而且能够掌握，但仅此不够，还需引导学生从这类基础问题出发，展开想象，去解决一些实际问题。先来总结一下某一点关于基本直线的对称点的坐标:

①A(x，y)关于x轴的对称点A'(x，-y);

②B(x，y)关于y轴的对称点B'(-x，y);

③C(x，y)关于直线x-y=0的对称点C'(y，x);

④D(x，y)关于直线x+y=0的对称点D'(-y，-x);

⑤P(x，y)关于直线x=a的对称点P'(2a-x，y);

⑥Q(x，y)关于直线y=b的对称点Q'(x，2b-y)。

1 有关光线问题

例1.一束光线通过点A(-2，4)，在直线L:2x-3y-6=0反射，反射光线经过点B(6，8)，求射入光线和反射光线所在的直线方程。

分析:从表面上看好象是物理光线问题，但实质上是点关于直线的对称问题。由几何光线知识可知:点A关于直线2x-3y-6=0的对称点A′在反射光线所在的直线上，即:反射光线在直线A′B上;同理，入射光线在直线AB′(点B′是点B关于直线2x-3y-6=0的对称点)上。

例2.一束光线通过点A(-3，2)照射到x轴上，经x轴的反射，反射光线与圆x2+y22-8x+6y=0相切，求反射光线所在的直线方程。

分析:首先找出点A(-3，2)关于x轴的对称点A′(-3，-2)，然后再求经过点A′(-3，-2)的圆x2+y22-8x+6y=0的切线方程，即反射光线所在的这直线就是所求的切线方程。

解:显然点A(-3，2)关于x轴的对称点为A′(-3，-2)，设过点A′(-3，-2)

与圆x2+y2-8x+6y=0相切的直线斜率为k，则切线方程为:y+2=k(x+3)，即kx-y-2+3k=0。根据圆的切线性质可知，圆心到切线的距离等于半径，圆x2+y2-8x+6y=0的圆心坐标为(4，-3)，半径等于5，从而圆心(4，-3)到切线kx-y-2+3k=0的距离

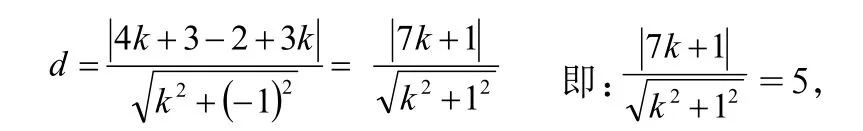
化简、整理得:12k2+7k-12=0，解得

从而反射光线所在的直线方程为:3x-4y+1=0。

2 有关最小值问题

例3.在一条公路同一边有2个村庄A、B，它们在同一直角坐标系下，坐标分别为A(-2，1)、B(3，4)，公路所在直线位置为3x-2y-6=0。现需在公路边建一个电力输送站，问输送站建在什么位置到A、B两村庄的输送线路最短？

分析:如果A、B村庄分别在公路的二边，那么直线段AB与公路的相交位置(M)就是要寻找的输送站的位置。现在A、B村庄在公路的同一边，根据两点之间距离最短的是直线段和对称性的知识可知，这个问题的实质仍为点关于直线的对称问题。村庄A关于公路(直线3x-2y-6=0)的对称点A′与B村庄的距离为|AM|+|BM|，因此直线段A′B与公路(直线3x-2y-6=0)相交的位置(M)，就是要找的输送站位置。因为此时的M位置能使|AM|+|BM|的值最小。求解过程:(1)先求出点A(-2，1)关于直线3x-2y-6=0的对称点A′的坐标，(2)求过A′、B两点的直线方程，(3)求直线A′B与直线3x-2y-6=0的交点M的坐标，则该交点M就是公路边建一个电力输送站位置。

3 有关几何图形的对称性问题

例4:△ABC的顶点A的坐标为(2，4)，∠B与∠C的平分线的方程分别为L1:x-y-2=0和L2:x+2y-5=0，求BC所在直线的方程。

分析:该题表面上求直线方程的条件不明显，但根据角平分线和点关于直线的对称有关知识，就可发现点A关于∠B，∠C的平分线的对称点都在BC所在直线上。求解过程:(1)求出点A关于∠B与∠C的平分线L1和L2的两个对称点A1、A2，(2)求直线A1A2方程，(3)BC所在的直线方程就是直线A1A2的方程。

解:先求点A关于∠B的平分线L1:x-y-2=0的对称点A1的坐标，显然L1:x-y-2=0 k=1的斜率，且AA1⊥L1，则直线AA1的斜率k=-1，

从而有:y-4=-1(x-2)，即直线AA1的方程为x+y-6=0，

从而A1的坐标为(6，0)。

同理:A2的坐标为(0，0)。(A2是点A关于∠C的平分线L2:x+2y-5=0的对称点)

则直线A1A2方程为y=0。

根据角平分线和点关于直线的对称的性质，可知点A关于∠B，∠C的平分线的对称点A1、A2都在BC所在直线上，所以BC所在的直线方程就是直线A1A2的方程，即:y=0。

例5:已知双曲线C:3x2-y2=1与直线L:y=kx+1相交于M、N两点，是否存在实数k，使M、N两点关于直线x-2y=0对称？

解:设M(x1，y2)、N(x2，y2)，且M、N的中点P(x0，y0)，假设存在实数k，使M、N两点关于x-2y=0对称，根据点关于直线的对称的性质，可知直线MN的斜率

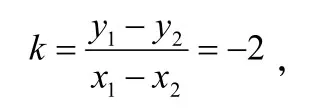
且点P(x0，y0)满足直线方程x-2y=0，即x0-2y0=0，

因为M、N两点在双曲线C:3x2-y2=1上，因此有

从而y0=0，x0=0。

即M、N的中点P的坐标为(0，0)，显然点P(0，0)不在直线MN(L:y=kx+1)上，

所以假设不成立，即不存在实数k，使M、N两点关于直线x-2y=0对称。