考虑缺陷因素的角接触球轴承七自由度动力学模型

周 智，朱永生，闫 柯，张优云

（1.宜昌测试技术研究所，湖北 宜昌 443003；2.西安交通大学 机械工程学院，陕西 西安 710049）

0 引言

主轴是数控机床的主要部件，其服役性能决定了零件成形的加工质量和机床的使用寿命及安全性。角接触球轴承作为机床主轴常用的支承部件，其旋转精度、热特性和动特性等关系着主轴的工作性能。角接触球轴承在工作的过程中往往承受着变化的轴向力和径向力，尤其是高速数控机床的角接触球轴承发热量大、工作温度高，在长期服役的情况下容易发生点蚀、疲劳、剥落等表面损伤。深入研究考虑缺陷的角接触球轴承的振动表征具有以下意义：①可以为机床主轴轴承的预紧力、润滑、冷却等设计和实时调控策略提供理论参考，防止轴承的缺陷继续发展，避免恶性事故发生，提高设备可靠性；②能根据缺陷的振动特点为研究轴承振动信号的特征提取方法提供参考；③通过角接触球轴承动力学模型获取的缺陷轴承振动信号，能够在没有实验样本的条件下，为智能诊断算法提供大量的机床轴承故障样本数据［1］。

目前，针对滚动轴承的振动特性研究主要以拟动力学模型和动力学模型为基础。在滚动轴承拟动力学模型（quasi-dynamic mechanical mode）方面，Harris［2-6］建立了轴承系统的运动微分方程，发展了球轴承的拟动力学模型，但该模型未考虑润滑的影响，因此不能准确反映轴承的振动特性。在考虑缺陷的轴承动力学模型（dynamic mechanical mode）方面，法国B.Mevel［7］、印度M.S.Patil［8］、伊朗Ahmad Rafsanjani［9］等考虑轴承的变柔度振动，建立了深沟球轴承二自由度模型，得出缺陷轴承在径向水平、垂直两个方向的振动响应；Aktärk等［10］建立了三自由度深沟球轴承动力学模型，研究了滚动体尺寸对轴承振动的影响。Harris［11］介绍了考虑滚动轴承的滚滑的4自由度滚动轴承模型，模拟了内、外圈损伤的振动响应；Liew 等［11］针对角接触球轴承展开研究，考虑轴向刚度提出5 自由度分析模型；Mohsen［13］从功率流角度出发，利用键合图方法建立了滚动轴承动力学模型。在国内，针对角接触球轴承的动力学模型研究较少，主要集中在深沟球轴承的动力学研究方面。张中民等［14］综合考虑深沟球轴承静态载荷分布、振动传递函数的影响，建立了单自由度缺陷轴承模型；杨将新和曹冲锋［15-16］等建立了分别具有外圈和内圈局部缺陷的深沟球轴承振动模型，对模型进行了动态仿真，但该研究基于线性模型，其分析结果仅适用于低速运转的滚动轴承及转子系统；张耀强等［17］考虑非线性轴承力和径向游隙、缺陷冲击力等非线性因素，建立了二自由度深沟球轴承动力学模型。但上述研究都没有考虑轴承座和高频共振的影响，因此无法真实反映轴承系统高频段共振现象。本文将在传统三自由轴承模型的基础上考虑缺陷的影响，综合探讨轴承座、传感器等传递路径中的高频共振，建立了角接触球轴承七自由度动力学模型，获取了轴承的动力学响应，并在轴承实验台上进行振动测试，对动力学模型进行实验验证。

1 角接触球轴承七自由度动力学模型

轴承系统是一个包括角接触球轴承、转轴、轴承座和测试传感器的复杂系统。本文建立的轴承系统动力学模型如图1所示，在传统的三自由度动力学模型基础上额外附加一个四自由度单位质量谐振器，可以模拟轴承座和传感器在两个径向方向的高频固有振动；m1，m2，m3，x1，x2，x3，y1，y2和y3分别表示内圈、轴承座和传感器质量、径向水平绝对位移以及径向垂直绝对位移；z1为内圈的轴向绝对位移；k2x，k3x，k2y，k3y，c2x，c3x，c2y和c3y分别表示轴承座和传感器径向水平方向、垂直方向的刚度和阻尼；c1表示轴承阻尼；Fx，Fy和Fz分别为轴承非线性支承反力在径向水平、垂直和轴向的分量；Wx，Wy和Wz分别为作用在转子上的径向水平力、垂直力和轴向力在轴承处的外力分量；m和e分别为偏心质量和偏心距；单个滚动体与内、外圈接触副的刚度K、阻尼c1的计算见式（7），滚动体的质量不计；c1x，c1y和c1z的计算见式（8）。则轴承内圈的运动方程为：

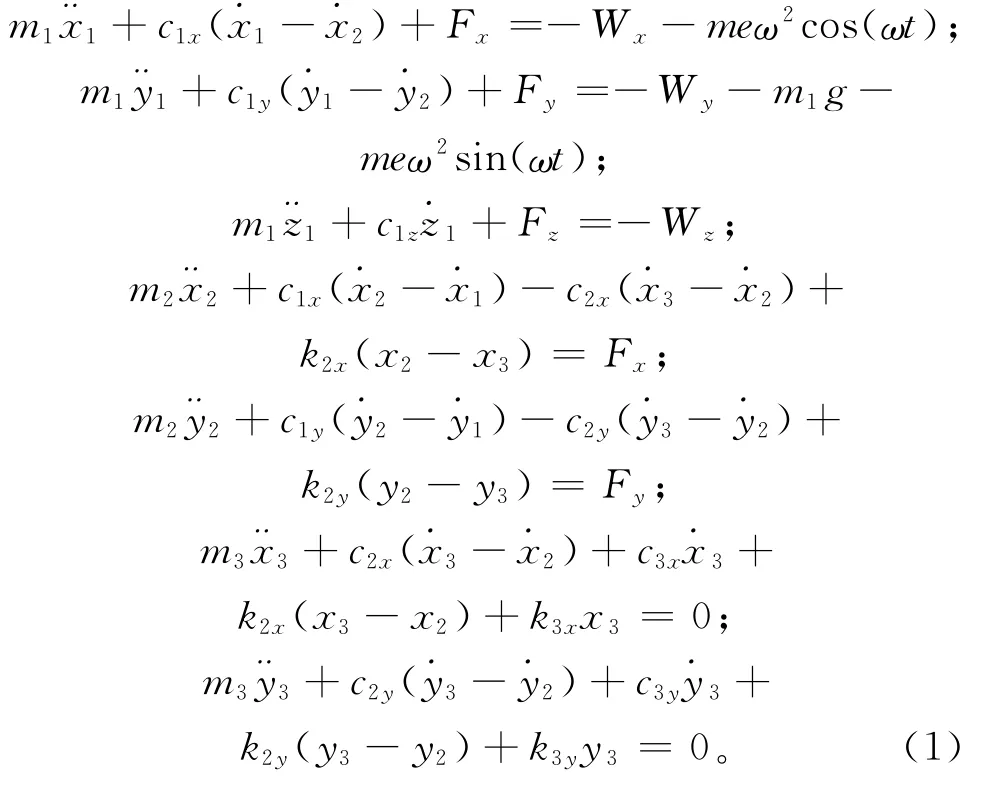
其中非线性轴承反力的表达式为

式中：NR为滚动体个数，K为滚动体与内、外圈的总体接触刚度（如式（3）），δj，θj和αj分别为第j个滚动体与内外圈的变形量、角位置和最终接触角（如式（4）～式（6））。

式中Ki和Ko分别为滚动体与内、外圈的接触刚度。

式中：A为内外圈沟道曲率中心距，z0为由于初始预紧力而导致的轴向变形量，γdj和Cd为缺陷因子（如式（9））和缺陷深度（如式10）。

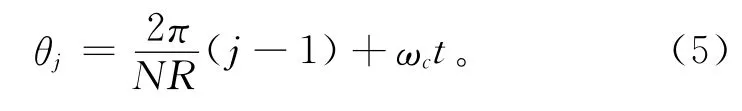
式中ωc为保持架的角速度。

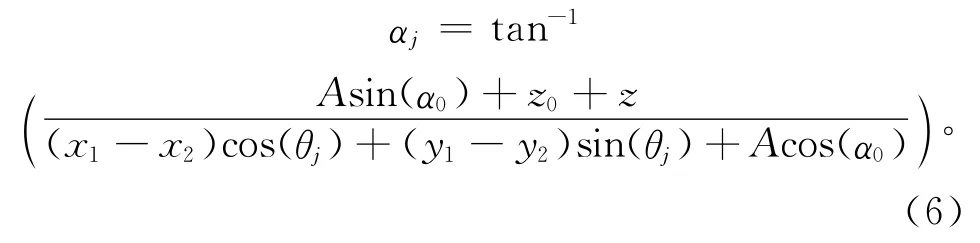
在机床高速运行过程中，轴承的润滑状态处于弹流润滑中，滚动体与内、外圈的接触面都将形成油膜，因此单个球接触时的总阻尼分为内、外圈油膜阻尼，赫兹接触区和出口区的阻尼忽略不计，主要考虑油膜入口区的阻尼，其表达式为

由单个球接触的阻尼公式，结合轴承三个方向的平动自由度，可以推导出整个球轴承的油膜阻尼表达式为

2 缺陷模拟方法

本文以内、外圈的疲劳剥落情况为研究背景，分析滚动体通过疲劳剥落产生缺陷坑区域时的游隙变化，进而改变滚动体与内、外圈之间的接触变形（如式（4））和轴承反力，从而影响滚动轴承的动力学响应。当轴承发生疲劳剥落时，将有一个凹坑产生，如图2所示，一般采用一个缺陷深度Cd和角距离Δφd来反映。本文采用缺陷因子γdj来判断第j滚动体是否运转到外圈缺陷区域，其表达式为

式中φd为缺陷角位置。外圈缺陷时，因为缺陷区域不发生变化，所以φd=φd0；内圈缺陷时，由于缺陷区域位置随着轴的转动而发生变化，φd=ωt＋φd0。式中：ω为轴的角速度，φd0为缺陷坑的初始角位置。

传统方法（如图3a）认为，当滚动体运行到缺陷区域时，滚动体瞬间处于非接触状态，缺陷深度为固定值，直至滚动体刚脱离出坑才结束，因此这种情况下的冲击相对于实际冲击值较大。而且在真实情况下，尤其是早期微弱缺陷初期，滚动体不会整体落入缺陷坑内，因此该方法不能真实反映缺陷情况下滚动体的真实运动轨迹。为了真实反映滚动体从刚进入缺陷坑和脱离出缺陷坑时滚动体的实际轨迹，缺陷深度Cd应是角度φ的函数，本文将其简化为半正弦函数（如图3b），此时可得

缺陷的角距离

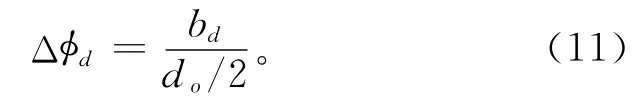
式中：bd为缺陷宽度，do为外圈沟底直径。

3 动力学模型的实验验证

为验证上述动力学模型的正确性，本文通过角接触球轴承实验台进行模拟实验，测试缺陷轴承的振动响应，对比动力学模型结果进行验证。实验台主要由模拟主轴、预紧力液压加载系统、驱动与电器控制系统及轴承测试系统组成，如图4所示。液压加载系统主要实现测试轴承预紧力的动态调整。主轴由通过变频器控制的变频电机驱动，由同步带实现传动。角接触球轴承的振动测试采用DYTRAN-3133A 三向加速度传感器。测试轴承HRB7206AC安装在右侧轴承座内，内圈直径为30 mm，外圈直径为62mm，节圆直径dm=46mm，轴承宽度为16 mm，滚动体直径Db=9.525 mm，滚动体个数NR=12，轴承接触角α=25°。为模拟缺陷对轴承的影响，采用电火花加工方法在角接触轴承的滚道表面上人为加工一个微小的凹坑，凹坑的宽度为0.3 mm。轴的转速为1 200r／min，轴的转频fr=20 Hz，预紧力为600N，采样频率为48kHz。此时由滚动轴承故障特征理论［18］可知，角接触球轴承的外圈故障特征频率fo=97.48Hz，内圈故障特征频率fi=142.52Hz，其计算公式如下：

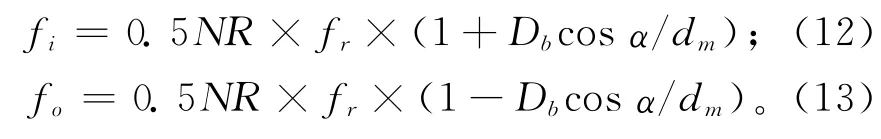
当内圈产生缺陷时，七自由度动力学模型的计算结果和实验结果对比如图5所示，其中包络谱的细节对比如图6所示。由结果可知，时域波形中模型和实验结果基本一致，轴承的振动响应为衰减的冲击信号，且冲击频率为内圈故障特征频率fi。频域中存在多个共振频带，尤其是在高频段存在共振。从包络谱的细节对比可知，当内圈存在缺陷时，包络谱中内圈缺陷频率fi及其倍频、边频带清晰可见，其中边频带（如fi-fr，fi＋fr等）是由于缺陷位置随着轴的旋转发生变化，进而冲击力的幅值被转频fr调制造成的。图7所示为外圈存在缺陷时轴承动力学模型和实验结果的对比。时域波形中模型和实验的结果基本一致，存在频率为fo的冲击衰减信号；频域中同样存在多个共振频带，尤其是模型也体现了高频共振；包络谱中外圈故障特征频率fo及其倍频清晰可见。综上所述，本文建立的动力学模型是正确的，能反映滚道存在缺陷时轴承的振动响应，且能体现由冲击激起的高频共振。

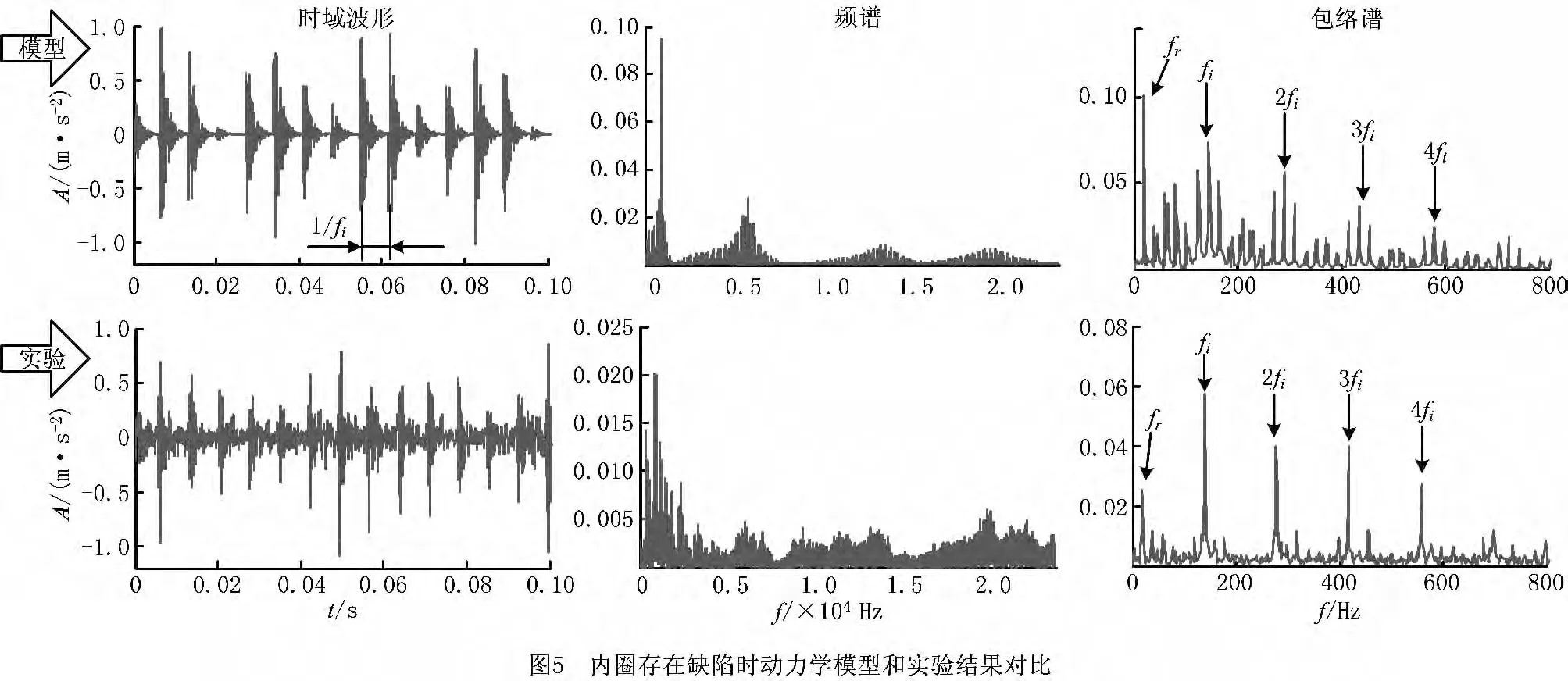
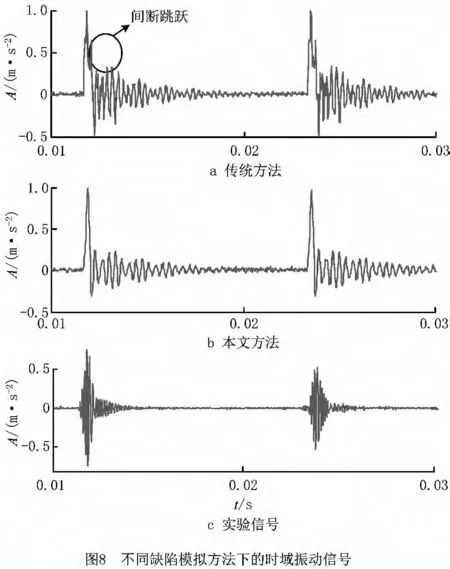
图8所示为不同缺陷模拟方法、轴承动力学模型下的时域振动信号。从传统的缺陷模拟方法（如图8a）的轴承模型计算的信号可以看出，从滚动体刚进入缺陷坑到滚动体将脱离出坑的过程中，轴承的振动表现为自由振动，然而当该自由振动还未衰减完时，因滚动体瞬间脱离出缺陷坑而又出现一个自由振动，整个过程中轴承游隙的变化是跳跃的，因此时域振动信号出现了跳跃。而从本文所提缺陷模拟方法（如图8b）下的轴承信号可以看出，滚动体刚进入缺陷坑到滚动体将脱离出坑的过程中，轴承的振动响应表现为强迫振动，在滚动体脱离出缺陷坑时出现一个自由振动，这是因为整个过程中缺陷深度的变化是连续的，所以时域振动信号是连续的，这与实验信号基本相符。由此可知本文所提的缺陷模拟方法是有效的。

4 结束语

数控机床的加工精度与使用寿命和机床主轴的角接触球轴承运行状态关系密切。在高速、超高速机床长期服役的情况下，轴承容易发生疲劳和点蚀等故障，在滚道和滚动体表面产生凹坑，导致振动水平过大。本文考虑轴承座和传感器系统传递路径中的高频共振特点，建立了考虑缺陷因素的七自由度动力学模型，提出更合理的缺陷模型方法并得到了轴承的振动响应。当角接触球轴承表面存在缺陷时，将产生一定特征频率的衰减冲击，而且高频段存在共振现象。最后对轴承实验台上的缺陷轴承进行了振动测试，通过计算结果和实验结果在时域、频谱和包络谱的对比分析验证了本文所建动力学模型的正确性。

后续研究将揭示预紧力、载荷、温度、润滑条件、缺陷程度等多工况因素对缺陷轴承动力学响应的影响规律，并构建机床轴承的故障样本库，结合智能诊断算法将其应用到机床轴承的状态监测和智能诊断中，建立机床轴承的状态预警机制、工况参数在线调控策略和机床的维修计划，确保机床的加工质量和可靠性。

［1］WANG Yuanhang，DENG Chao，WU Jun.Heavy machine's fault diagnosis based on mixed expert system［J］.Computer Integrated Manufacturing Systems，2010，16（10）：2139-2147（in Chinese）.［王远航，邓 超，吴 军.基于混合型专家系统的重型机床故障诊断［J］.计算机集成制造系统，2010，16（10）：2139-2147.］

［2］HARRIST A.Rolling bearing analysis［M］.New York，N.Y.，USA：John Wiley&Sons，2001.

［3］HARRIS T A，MINDEL M H.Rolling element bearing dynamies［J］.Wear，1973，23（3）：311-337.

［4］HARRIS T A.Ananalytical method to predict skidding in thrust-loaded，angular-contact ball bearings［J］.Journal of Tribology，1971，93（1）：17-24.

［5］HARRIS T A.Ball motion in thrust-loaded，angular-contact bearings with coulomb friction［J］.Journal of Tribology，1971，93（1）：32-38.

［6］HARRIS T A，BARNSBY R M，KOTZALAS M N.A method to calculate frietional effects in oil-lubricated ball bearings［J］.Tribology Transactions，2001，44（4）：704-708.

［7］MEVEL B，GUYADER J L.Experiments on routes to chaos in ball bearings［J］.Journal of Sound and Vibration，2008，318（3）：549-564.

［8］PATIL M S，JOSE M，RAJENDRAKUMAR P K，et al.A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing［J］.International Journal of Mechanical Sciences，2010，52（9）：1193-1201.

［9］RAFSANJANI A，ABBASION S，FARSHIDIANFAR A.Nonlinear dynamic modeling of surface defects in rolling element bearing systems［J］.Journal of Sound and Vibration，2009，319（3）：1150-1174.

［10］AKTÄRK N，GOHAR R.The effect of ball size varia-tion on vibrations associated with ball bearings［J］.Journal of Engineering Tribology，1998，212（2）：101-110.

［11］HARRIS T A.Rolling bearing analysis［M］.4th ed.New York，N.Y.，USA：John Wiley&Sons，2001.

［12］LIEW A，FENG N，HAHN E.Transient rotor dynamic modelling of rolling element bearing systems［J］.Journal of Engineering for Gas Turbines and Power，2002，124（4）：984-991.

［13］NAKHAEINEJAD M，BRYANT M D.Dynamic modeling of rolling element bearings with surface contact defects using bond graphs［J］.ASME Journal of Tribology，2011，133（1）：1-12.

［14］ZHANG Zhongmin，LU Wenxiang，YANG Shuzi，et al.A model for the vibration produced by local faults in roller bearing and its application［J］.Journal of Huazhong University of Science &Technology，1997，25（3）：50-53（in Chinese）.［张中民，卢文祥，杨叔子，等.滚动轴承缺陷振动模型及其应用研究［J］.华中理工大学学报，1997，25（3）：50-53.］

［15］YANG Jiangxin，CAO Chongfeng，CAO Yanlong，et al.Mod-el for dynamic characteristics produced by inner race localdefect in ball bearing system and its simulation［J］.Journal of Zhejiang University，2007，41（4）：551-555（in Chinese）.［杨将新，曹冲锋，曹岩龙，等.内圈局部损伤滚动轴承系统动态特性建模及仿真［J］.浙江大学学报，2007，41（4）：551-555.］

［16］CAO Chongfeng，SONG Jingwei，WANG Qiuhong.Dynamic characteritics for the part fault of outer race in a ball bearing and computer simulation［J］.Journal of East China Jiaotong University，2005，22（2）：123-126（in Chinese）.［曹冲锋，宋京伟，王秋红.滚动轴承外圈局部缺陷的动态特性及计算机仿真［J］.华东交通大学学报，2005，22（2）：123-126.］

［17］ZHANG Yaoqiang，CHEN Jianjun，TANG Liuding.Nonlinear dynamic characteristics of rolling element bearing with localized defect on outer ring［J］.Acta Aeronautica et Astronautica Sinica，2009，30（4）：751-756（in Chinese）.［张耀强，陈建军，唐六丁.考虑外圈局部缺陷的滚动轴承非线性动力特性［J］.航空学报，2009，30（4）：751-756.］

［18］PATIL M S，JOSE M，RAJENDRA KUMAR P K.Bearing signature analysis as a medium for fault detection：a review［J］.Journal of Tribology，2008，130（1）：1-7.