基于多失效模式相关分析的技术特征综合配置方法

杜 雷，高建民，陈 琨+，姜洪权

（1.西安交通大学 机械制造系统工程国家重点实验室，陕西 西安 710049；2.台州学院 机械工程学院，浙江 台州 318000）

1 问题的提出

机械零部件的失效原因和机理同时来自内部退化和外力影响，如磨损退化、腐蚀、疲劳、断裂和过载等。失效模式可以分为软失效（soft failures）和硬失效（hard failures）两种形式［1］。软失效是由于设备长期服役造成的性能衰退，硬失效是由于软失效的扩展或者瞬间应力过大造成的破坏性故障。多种失效机理和失效过程通常存在复杂的关联关系，而且软失效模式还可能诱发其他软失效模式形成连锁失效，最终引发硬失效，即同一零件上的连锁失效可能会呈现与机电系统故障网状传播扩散方式［2］类似的现象。长期以来，由于缺乏对上述失效机理、软失效和硬失效三者之间复杂关联关系进行描述和分析的有效工具，普遍存在着可靠性设计与性能设计相脱节的现象，其后果是设计参数的配置值不能保障产品的可靠性。

可靠性设计与不确定因素紧密相关，在一阶／二阶矩可靠性计算的通用方法［3］被提出后，概率设计［4-5］在机械可靠性设计中获得了广泛应用。基于概率设计的应力-强度干涉模型［6-7］是目前普遍使用的机械可靠性设计方法，国内外学者基于该模型对零件和系统的可靠性计算方法做了大量研究。应力-强度干涉模型的原理是根据经验数据、故障树分析（Fault Tree Analysis，FTA）或失效模式和效果分析（Failure Mode and Effects Analysis，FMEA）／故障模式、影响及危害性分析（Failure Mode Effects and Criticality Analysis，FMECA），确定可靠性关键件和重要件及其相应的失效形式，然后针对其主要失效形式（薄弱环节）建立连接方程或极限状态方程，求解设计参数值。然而在实际使用中，FTA，FMEA／FMECA 等可靠性分析工具存在表达不够严密、缺乏一致性和只考虑单一失效模式等局限性。虽然有研究者考虑复杂系统零部件多失效模式联合作用对整个系统的影响，提出基于多失效模式的FMEA［8］，但仍然存在建模过程复杂、计算复杂等缺陷。同时，上述方法只针对零部件主要失效模式进行概率设计，忽略了零件多失效模式之间的相关性影响，存在较大的不合理性。

20世纪90年代出现了可靠性功能配置（Reliability Function Deployment，RFD）的概念［9］，其基本原理是将质量功能配置（Quality Function Deployment，QFD）与FTA 和FMECA 等工具有机集成，利用多层矩阵分解方式将用户的可靠性需求逐层转化为产品零部件相应的产品技术特征，弥补了QFD 技术在质量规划中没有考虑产品后期的故障及其影响方面的缺陷［10］。文献［11］以RFD 思想为基础，利用“多米诺”矩阵对零部件间的故障传播路径和趋势进行了定性和定量地描述与分析，并在此基础上改进了传统的可靠性分配方法。可以发现，RFD 的优势是将传统的可靠性分析方法从填表方式转变为以矩阵结构相关性分析为主的方式，以矩阵分解的方法自顶向下地控制产品的可靠性，其矩阵结构能够指出系统复杂性不同的处理层次，对设计要素之间关系的描述更为清晰和简洁。同时，RFD 过程还可以利用QFD 中已有的数字运算和归一化处理方法进行数值计算［12］。因此，将RFD 的矩阵结构用于描述失效机理与失效模式的关联关系，以及软硬失效模式间的网状传播路径，具有表达严密、计算方便的优点，能够有效地对多失效模式之间的相互影响进行评估和计算。

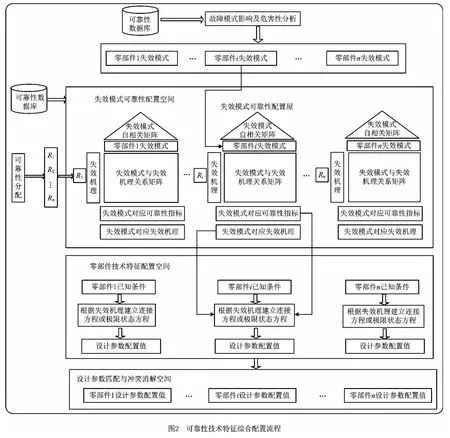
综上所述，针对传统可靠性概率设计的局限性，本文提出一种考虑多失效模式相互关联耦合关系的零部件技术特征综合配置方法。首先，建立基于RFD 的可靠性配置屋，利用其矩阵结构描述各零部件失效机理、软失效和硬失效三者之间的关联关系，最终形成由多个可靠性配置屋组成的失效模式可靠性配置空间；其次，在可靠性配置空间的分解矩阵中，综合考虑零部件多失效模式的相关性，将每个零部件总的可靠性指标值分解配置给该零部件的各个失效模式；然后，按照该失效模式的主要失效机理建立连接方程或极限状态方程，构成技术特征配置空间，在技术特征配置空间中将各个失效模式可靠性指标配置值和其他已知条件代入方程，使用逆可靠度法［13］解算相应的技术特征设计参数值；最后，考虑各个零部件间的设计参数值存在相互影响因素，将设计参数配置值输入到设计参数匹配与冲突消解空间，按照一定的匹配与冲突消解规则处理后，输出最终配置值。

2 可靠性配置屋的构建与技术特征综合配置流程

2.1 构建失效模式可靠性配置屋

失效机理与软、硬失效模式之间的关系如图1所示。从图中可以观察到，失效机理可以同时与软硬失效模式发生联系，软失效模式可以引起其他软失效或者直接引发硬失效。同时，还存在由多个失效原因引起的“共因失效”，失效机理与软、硬失效模式三者之间呈现复杂的网状关系；另一方面，某些软失效可能只是轻微地影响零件的性能，而另一些软失效则可能持续地发展和扩散，进而导致硬失效，对整个零件的性能产生重大影响。也就是说，各个失效模式对零件造成的可靠性损失是不同的。

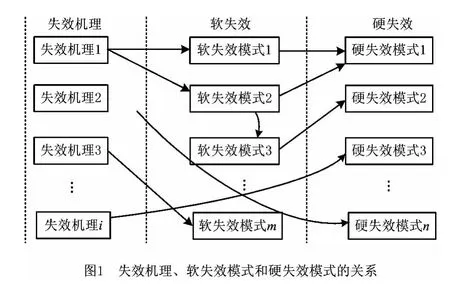
RFD 的核心思想是将可靠性分析工具与质量屋的矩阵结构有机地集成应用，可靠性屋（House of Reliability，HOR）［14］是实现RFD 思想和方法论的工具，它提供了把可靠性概念或要求逐层转化为相应的可靠性参数特性和设计措施的框架和结构。为有效表达失效机理失效模式以及软、硬失效模式之间的关联关系，本文以HOR 为工具，建立了零部件失效模式的可靠性配置屋。在可靠性配置屋中，利用失效模式与失效机理关系矩阵描述失效机理与失效模式间的关系，利用失效模式自相关矩阵（多米诺矩阵）描述软、失效模式之间的扩散传导路径。由于矩阵的二维平面性，可以精确、简洁地描述失效机理、软失效和硬失效三者之间的网状关联关系。在此基础上，建立相应的数学模型，计算零部件每个失效模式的可靠性损失，并以此为依据，将零部件的可靠性指标值进一步分配给该零部件的各个失效模式。

机械零部件的失效机理一般分为以下几种类型［4］：

（1）退化耗损型 如磨损、腐蚀、老化、微小裂纹等，属于软失效范畴。

（2）损坏型 如断裂、变形过大、裂纹、点蚀等，属于硬失效范畴。

其他失效机理还有松脱型、失调型、堵塞渗漏型等。从减少分析复杂性角度考虑，本文选择主要失效机理建立失效模式可靠性配置屋。该可靠性配置屋由三个矩阵组成：

（1）零部件失效机理与失效模式的关系矩阵U｛uij｝。

（2）失效模式自相关矩阵P｛pij｝。

（3）失效机理的可靠性损失权重矩阵W｛wi｝。

矩阵U｛uij｝中，元素uij表达了在零部件层级上失效机理与软、硬失效模式之间的关系。当uij=0时，表示失效机理i不会引发失效模式j；当uij≠0时，uij的值表示失效机理i引发失效模式j的可能性的大小，本文中uij的评估值按弱、中等和强分为三个等级，分别取整数1，3和9。

pij为失效模式自相关矩阵P｛pij｝的通项，表示同一零部件上各个失效模式pi与pj的相互影响关系。当pij=0时，表示失效模式i与失效模式j之间无关联关系；当pij≠0时，pij的值表示失效模式i引发失效模式j的概率，反之亦然。一般情况下，pij≠pji。

失效机理权重矩阵W｛wi｝的元素wi表示失效机理i引发软、硬失效造成可靠性损失的大小程度，可由评价人员根据相关的可靠性统计数据获得。文中失效机理权重大小由整数1～9表示，按照引发失效造成可靠性损失从小到大排列。

2.2 技术特征综合配置流程

按照RFD 的基本原理，并考虑机械零件参数设置值的相互影响，建立如图2所示的零部件技术特征综合配置流程，整个流程分以下三个阶段展开：

（1）第一阶段 在产品可靠性分配与FMECA分析的基础上，建立各个零部件的失效模式可靠性配置屋群，组成各零部件的失效模式可靠性配置空间；在每个零部件的失效模式可靠性配置屋的矩阵结构中，计算各失效模式造成的可靠性损失；按可靠性损失的大小，将零部件可靠性指标值分配给该零部件的各个失效模式，同时输出各个失效模式对应的主要失效机理。

（2）第二阶段 以第一阶段的配置结果为输入，建立各个零部件的技术特征综合配置空间。在该空间中，对每个零部件的主要失效形式按其主要失效机理建立连接方程或极限状态方程，并解算设计参数值。

（3）第三阶段 以第二阶段的配置结果为输入，建立设计参数匹配和冲突消解空间。在该空间中，按一定规则对各个零部件的设计参数配置值进行匹配和冲突消解，获得最终的设计参数配置值。

上述配置过程综合应用RFD 理论、基于概率设计的逆可靠度法以及冲突消解技术，将机械零件可靠性设计过程整合为分阶段的数据处理和计算流程。利用RFD 方法的矩阵分解结构将零部件的可靠性指标进一步分配给各个失效模式，最终使用逆可靠度法建立可靠性指标与机械零部件设计参数值之间的映射关系，使机械零件可靠性设计与性能设计实现了更紧密的结合，具有较好的系统性、层次性和实用性。

3 基于多失效模式相关的技术特征配置数学模型

3.1 失效模式的可靠性指标值分配

在产品层级将总可靠度分配给各零部件后，如果已知应力、强度的分布，则查分布表可得与零部件可靠度对应的可靠性指标β［4］。将β作为失效模式可靠性配置空间的输入，建立失效机理与失效模式的关联矩阵，在考虑失效模式之间相关性影响的情况下，评估各失效模式的可靠性损失。进而按照可靠性损失的大小，将零部件总的可靠性指标β分配给各个失效模式。

如果某失效模式i为独立发生的，造成可靠性损失为FLi，则有

式中：wj为与失效模式i对应的失效机理j可靠性损失权重；uij为失效模式i与失效机理j的关联系数。

假设某软失效模式i直接引发k个关联失效模式（k=1，2，…，m），k个关联失效对应t个失效机理（t=1，2，…，m），考虑失效单层连锁的影响，可得失效模式i的可靠性损失计算公式为

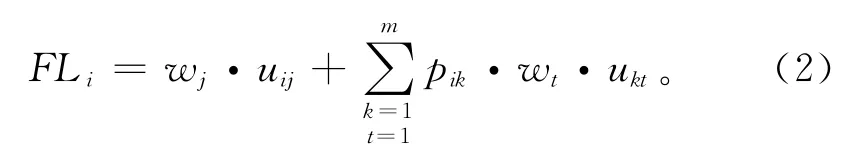
式中：pi，k=0，∀i=k；pik为第i个软失效模式引发第k个关联失效模式的概率；wt为与失效模式k对应的失效机理t可靠性损失权重；ukt为第k个失效模式与第t个失效机理之间的关联系数。

考虑到可靠性屋矩阵形式的结构，式（2）可以表示成如下矩阵式

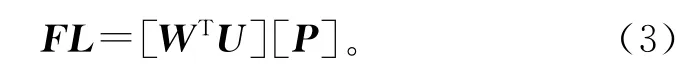
式中：pi，k=1，∀i=k；FL为1×m失效可靠性损失行向量；P为m×m自相关矩阵；W为n×1权重列向量；U为n×m关系矩阵。

式（3）只考虑了失效模式传播链中单层失效的影响，即软失效模式i直接引发k个关联失效模式的情况。当关联失效模式继续传播、引发连锁反应并最终导致硬失效时，失效模式传播层数f≥2，在计算失效模式可靠性损失时，要累加上其间接引发后续各个失效模式的影响。综合考虑多层失效模式的传播影响，式（3）可以进一步表示为

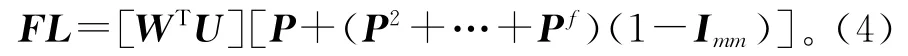
式中：pi，k=1，∀i=k；Imm为m×m单位矩阵；f为失效模式连锁层数。

从式（4）可以看出，失效连锁越长，作为失效发起端的失效模式的可靠性损失累积值就越大。对求得的各失效模式的可靠性损失进行归一化，得到如式（5）所示的各失效模式的可靠性指标配置系数αi，失效模式造成可靠性损失越大，可靠性指标的配置系数就越大。

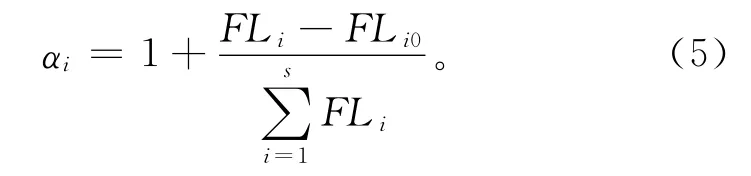
式中：FLi0表示该失效模式未计入失效模式相关时的可靠性损失，s是与该失效模式一起构成传播链的失效模式的数量，各失效模式的可靠性指标配置值β＊i由式（6）计算。

式中β为整个零件的可靠性指标值。根据HOR 的信息可以获得对应的主要失效机理，将和对应的主要失效机理同时输入零部件可靠性保证技术特征配置空间，再进行下一步技术特征参数值的配置。

3.2 基于逆可靠度法的技术特征参数值配置

应力-强度干涉模型是将应力分布、强度分布和可靠度在概率的意义下联系起来，构成一种设计计算的依据。假设强度S与应力s均为正态分布，强度大于应力的概率（可靠度）可表示为式中Z为功能函数，Z=S-s，Z＞0。根据应力-强度理论，有

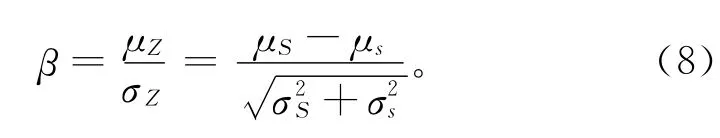
式中：μZ和σZ分别为Z的均值和标准差；μS和σS分别为强度的均值和标准差；μS和σS分别为应力的均值和标准差。式（8）将应力分布参数、强度分布参数和可靠度直接联系起来，称为连接方程［4］。β被称为可靠性指标，当知道应力和强度的分布参数后，就可算得β的值。

对于给定的目标可靠性指标βt，寻找设计参数θ的确定解的问题称为逆可靠度法。根据参数值的分布类型有以下两种求解方法［15-17］：

（1）若强度与应力均为正态分布，则可以在建立极限状态方程G（u，θ）后，使用基于一次二阶矩法的迭代法［18］求解。

（2）若强度与应力非正态分布，则可根据JC法［19］对非正态变量作当量正态化处理。然后建立极限状态方程G（u，θ），使用迭代法求解。

迭代法的计算方法可以表示为［18］：

对于G（u，θ）=g（x，θ），希望找到一个参数θ，使求解极限状态方程G获得的可靠度指标β等于预先给定的目标可靠度指标βt。其中：G（u，θ）为从极限状态方程原空间g（x，θ）到标准空间的转换，u为标准正态变量，x为基本随机变量，θ为待定的零部件设计参数。

对于给定的目标可靠度指标βt，上述逆可靠度问题可表述为寻找参数θ，使目标函数最小，即：

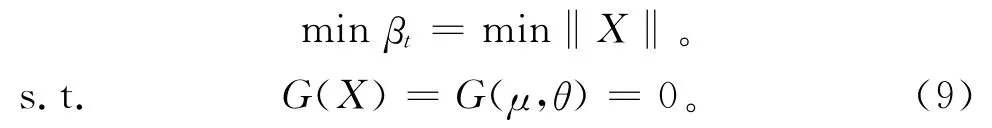
式中：X=（u，q）为基本变量组成的列向量；θ为所求的设计变量；u为除设计变量θ外，其余变量组成的向量。假设基本变量X为标准正态分布，其求解方法如下：

（1）求解最大失效概率对应的设计验算点μ＊

利用一次二阶矩方法，先假定各个变量设计验算点μ＊的迭代初始值；一般情况下可取其均值，然后根据式（10）经迭代后求出满足目标可靠性指标的设计验算点μ＊：

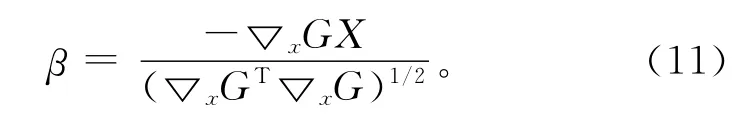
（2）利用迭代法求解设计变量θ

式（10）和约束条件G（u，θ）=0 将被用于求解逆可靠度问题。由于设计变量的均值θ发生变化将影响其设计验算点的值，可以认为极限状态函数值与θ有关。假设一个θ的初始均值为θ0，其值可根据设计经验进行预估，将G（μ，θ）=0对θ在θ0处做泰勒展开：

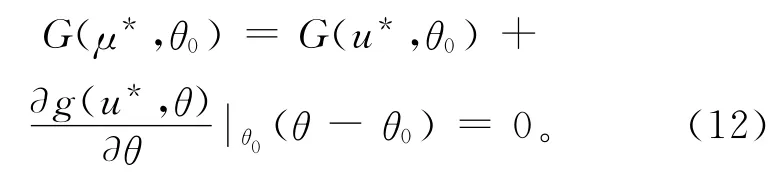
由式（12）可得

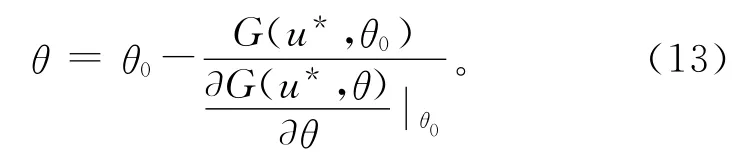
（3）迭代收敛的判断

在设定了设计验算点的初始值μ＊0 和设计变量均值的初始值θ0后，可以利用式（10）和式（13）获得下一次迭代值，判断是否收敛，如果前后两次迭代满足式（14），则本次的θ即为所求值，迭代终止；否则，用上次迭代求得的μ＊和θ进行下一次迭代。

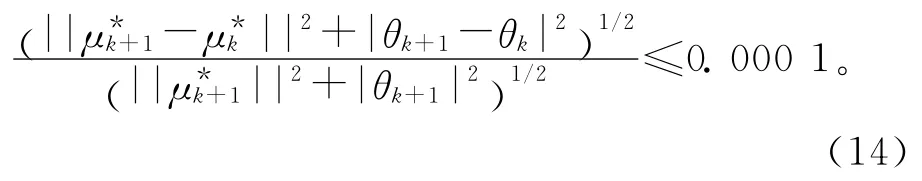
4 实例

本文选择某系列立式加工中心传动系统进行实例验证。该传动系统采用交流调频电动机，连续输出功率为7.5kW。主轴具有两档速度，低速档转速为876r／min～1 500r／min，高速档转速为1 500r／min～500r／min。采用齿轮二级变速传动，传动比为4∶1的低速传动和传动比为1∶1的高速传动两种变速机构，采用拨叉变速。

通过整理分析该加工中心从2008 年8 月～2009年12月收集的故障数据，并进行FMECA，建立相应的失效模式可靠性配置屋与零部件技术特征配置屋。限于篇幅，本文仅对该传动系统中花键传动轴设计参数进行配置。

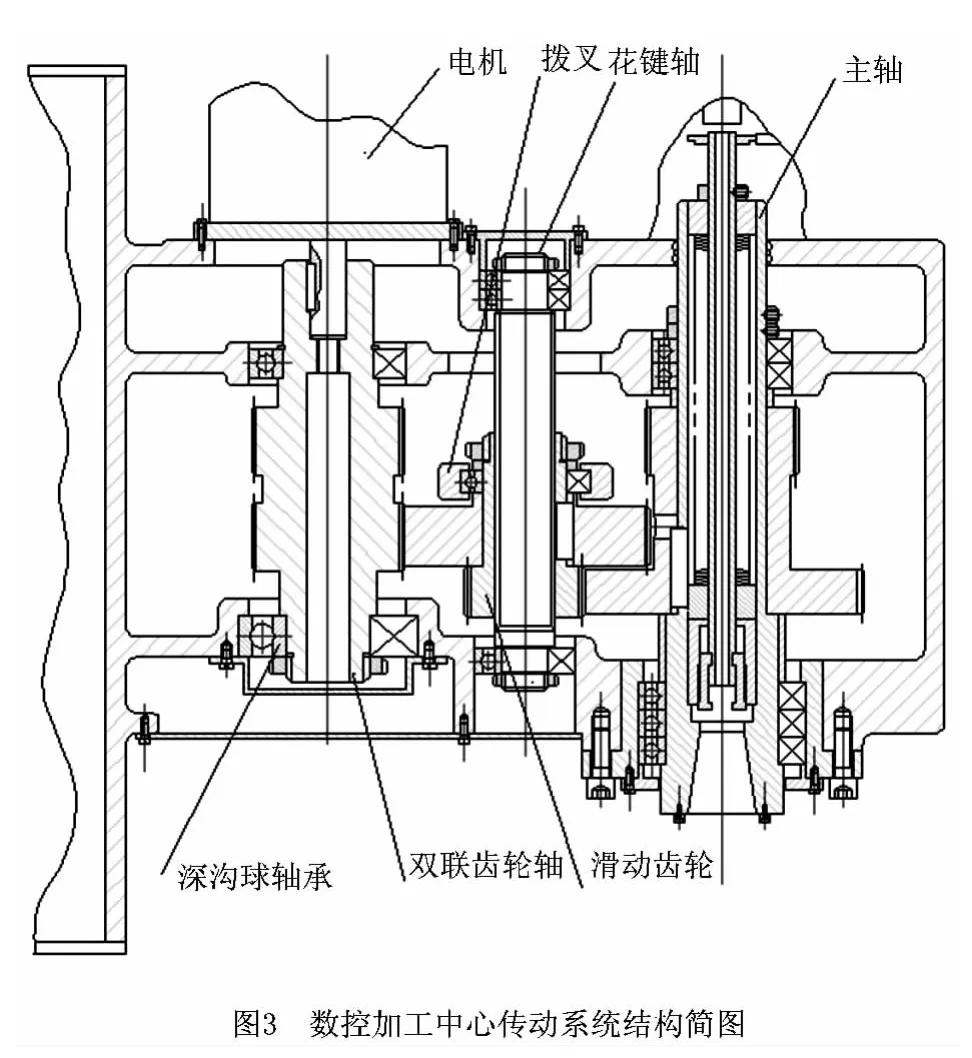
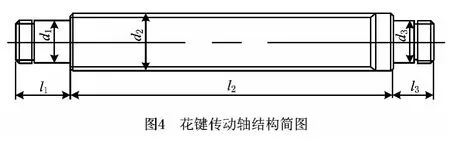
花键传动轴结构示意图如图4所示，滑动齿轮可以在轴上轴向滑动。已知条件为：传递转矩T=218 000N·mm，σT=10 000N·mm·mm，危险截面弯矩M=77 300N·mm，σm=5 000N。材料选用45＃钢调质处理，材料强度μS=800MPa，σS=80MPa。该轴承受稳定循环变应力，要求可靠度R=0.999。假设设计对象的应力与强度分布均为正态分布，查正态分布表可得花键轴的可靠性指标值β=3.1。

4.1 建立花键传动轴失效模式可靠性屋

通过FMECA 获取花键轴的8个失效模式，建立如图5 所示的花键轴失效模式可靠性配置屋。HOR 的矩阵分解结构将可靠性指标值β=3.1分配给图示的8个失效模式，输出各个失效模式的可靠性指标配置值，及其对应的主要失效机理。

在图5所示的失效机理与失效模式关系n×m矩阵中，可以清晰地表示该花键轴失效机理与软、硬失效模式之间的关联关系。例如：过载可能同时引起塑性变形和断裂，属共因失效现象；在失效模式m×m自相关矩阵中，可以描述软、硬失效模式之间的关联关系和传播方向，如数值0.8表示表面点蚀与疲劳裂纹之间关联关系的大小，而数值0.8处于下面三角形中表示由疲劳裂纹引发了表面点蚀。相反，表面点蚀引发疲劳裂纹则不成立。在自相关矩阵的二维平面上，可以观察到失效模式传播触发路径有以下几条：

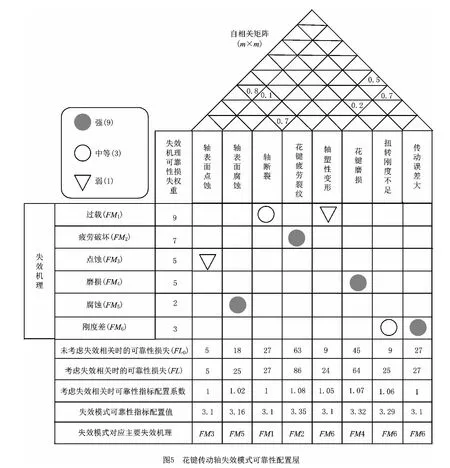
（1）表面腐蚀→疲劳裂纹→断裂。

（2）表面腐蚀→疲劳裂纹→点蚀。

（3）花键磨损→传动误差大。

（4）扭转刚度不足→塑性变形→传动误差大。

在以上触发路径中，失效模式传播的最大层数f=2。利用式（4）计算在考虑失效模式相关性的情况下各失效模式的可靠性损失FL，可以发现疲劳裂纹、花键磨损和扭转刚度不足这三个失效模式的可靠性损失增加值较大。其中疲劳裂纹虽然是软失效，但由于它处在触发链的起始端，在计入引发后续失效模式造成可靠性损失的累积影响后，可靠性损失增加了36%，因此其配置系数也从1 增加到1.08。各个失效模式对应的主要失效机理也被识别出来，并与可靠性指标配置值一起作为零部件技术特征配置空间的输入，进入下一步技术特征参数值的配置过程。

4.2 花键传动轴可靠性技术特征可靠性综合配置

根据花键轴可靠性配置屋的输出结果，发现花键疲劳裂纹与磨损造成的可靠性损失较大，其对应的设计参数分别为花键轴直径d2和花键部分的磨损寿命t。因此，本文针对花键传动轴建立疲劳裂纹与磨损失效模式的连接方程，并利用逆可靠度法求解相应设计参数的配置值。

4.2.1 疲劳裂纹失效可靠性技术特征配置

疲劳裂纹的失效机理是疲劳破坏。疲劳破坏是一个累积损伤的过程，可以分为裂纹形成、裂纹扩展和迅速断裂等阶段。疲劳裂纹的失效判据是在使用寿命期内不出现宏观工程可检裂纹，本算例中易产生疲劳裂纹的危险部位在花键部分，由于花键轴具体参数（如齿数、大径、小径等）未确定，因此选择花键部分平均直径d2为配置参数。根据第四强度理论，轴的弯矩M与扭矩T的合成应力s为

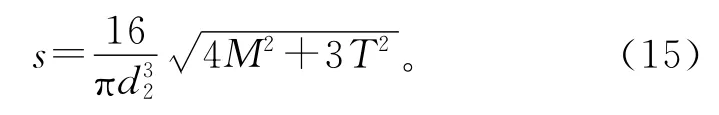
极限状态方程可表示为

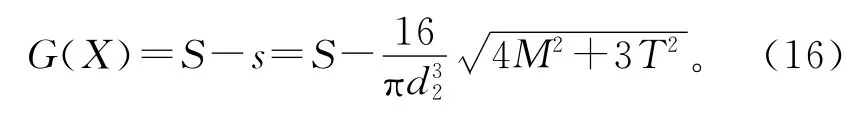
花键传动轴选用的材料强度μS=800 MPa，σS=80 MPa，，并服从正态分布。根据3σ法则可知，该材料的强度极限为δ=800±240 MPa，即该材料的最低强度δmin=560 MPa，如果该轴承受的弯曲拉应力小于δmin，并达到可靠性设计要求，则该轴段的设计将是安全的。因此，取S=δmin=560MPa，极限状态方程可表示为

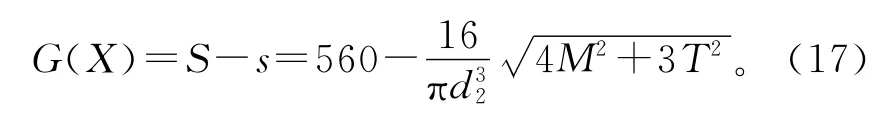
已知σT=10 000 N·mm，σm=5 000 N·mm，β＊=3.35。取M与T的均值为迭代初始值=218 000N·mm，=77 300N·mm，取轴径的迭代初始值将式（17）代入式（10），求得M与T的下一次迭代值与；然后，将代入式（13），求得轴径d2的下一次迭代值；如此反复迭代计算，直至轴径计算值符合收敛条件为止，迭代结果如表1所示（单位：轴径为mm，弯矩、扭矩为N·mm）。

表1 轴径d2的迭代计算结果

表2是考虑多失效模式相关时的概率设计与传统概率设计方式的计算结果对比。可以发现：由于考虑了失效模式的相关性带来的额外可靠性损失，轴径配置值从18.22mm 上升到18.91mm，增加了3.8%。配置值将被输入设计参数匹配与冲突消解空间中，按技术标准和特定的规则，与滑动齿轮的内花键配置参数值进行匹配和圆整。

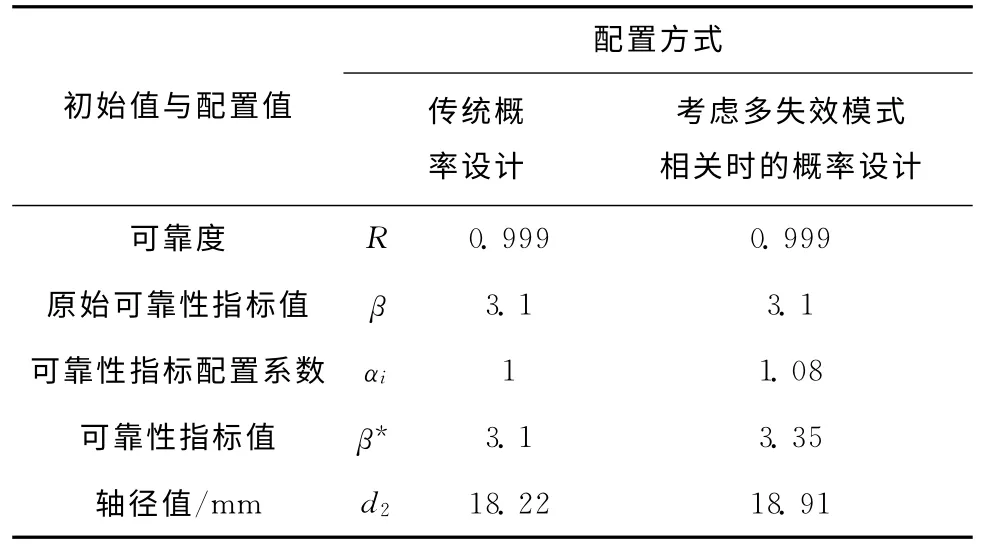
表2 计算结果比较

4.2.2 磨损失效可靠性技术特征配置

由摩擦造成的摩擦副表面材料质量的损失量，称为磨损量，用符号W表示，单位为μm。磨损量是时间的函数，其随时间的变化率称为磨损速度u，单位为μm／h。磨损的概率计算是在常规磨损计算的基础上，考虑参数的分散特性进行的，其可靠度计算的基本原理同样是强度-干涉理论［4］。假设磨损参数符合正态分布，建立的花键磨损失效极限状态方程为

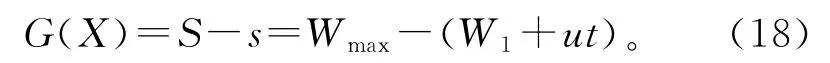
式中：Wmax为最大允许磨损量，W1为机器磨合阶段初始磨损量，u为磨损速度，t为磨损寿命。假设Wmax=16μm，极限状态方程可表示为

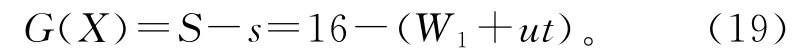
已知W1=6μm，μ=0.02μm／h，σW1=0.1μm，σμ=0.00 277μm／h，β＊=3.32。取W1与μ的均值为迭代初始值，即W＊10=6μm，μ＊0=μ=0.02μm／h，取轴径的迭代初始值t＊0=280h，将式（19）代入式（10），解算可 得W1与μ的下一 次迭代 值与；将和代入式（13），可以求得磨损寿命t的下一次迭代值；经反复迭代计算，求得磨损寿命t=285h。

表3所示为考虑多失效模式相关时的概率设计与传统概率设计方式的计算结果对比。可以发现：由于可靠性指标值的增加，磨损寿命从传统概率设计的300h下降到285h，减少了5%。在后续的工艺设计中，可以通过选择适当的表面强化处理手段保证磨损寿命t的值。磨损寿命配置值也将被输入设计参数匹配与冲突消解空间中，按技术标准特定的规则，与滑动齿轮的内花键磨损寿命值进行匹配。

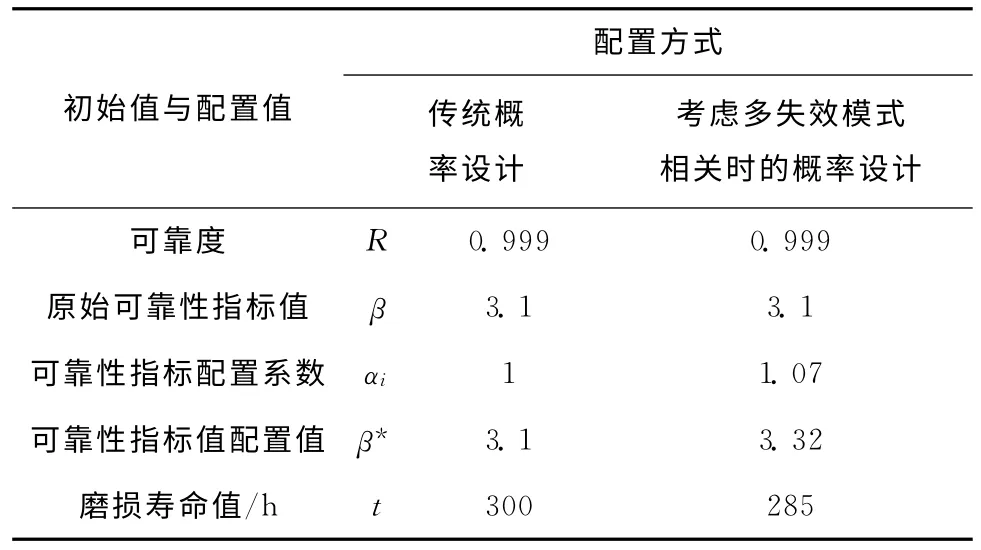
表3 花键轴磨损寿命计算结果

5 结束语

本文提出一种基于多失效模式相关分析的可靠性技术特征综合配置方法，该方法利用RFD 可靠性屋的矩阵分析结构描述失效机理、软失效和硬失效网状扩散传导关系。建立了计算零部件各失效模式可靠性损失的数学模型，采用该模型计算出的各失效模式可靠性损失考虑了软硬失效模式之间的相关性。将各失效模式可靠性损失进行归一化，获得各失效模式的可靠性指标配置系数，按照失效机理建立技术特征配置空间，最终将零部件可靠性指标分配给各失效模式。在技术特征配置计算模型中引入基于一次二阶矩的逆可靠度法，将失效模式可靠性指标配置值代入连接方程或极限状态方程，对关键零部件的可靠性技术特征参数进行综合配置。将该方法应用于某型加工中心传动系统花键轴的可靠性设计，实例表明，该方法能够对常规概率设计结果进行有效调整和优化。后续的研究重点是设计参数配置值匹配和冲突消解规则的制订，以及相应的算法实现等工作。

［1］JIANG Lei，FENG Qianmei，COIT D W.Reliability analysis for dependent failure processes and dependent failure threshold［C］／／Proceedings of Annual Reliability and Maintainability Symposium.Washington，D.C.，USA：IEEE，2011：339-345.

［2］JIANG Hongquan，GAO Jianmin，CHEN Fumin，et al.Vulnerability analysis to distributed and complex electromechanical system based on network property［J］.Computer Integrated Manufacturing Systems，2009，15（4）：792-796（in Chinese）.［姜洪权，高建民，陈富民，等.基于网络特性的分布式复杂机电系统脆弱性分析［J］.计算机集成制造系统，2009，15（4）：792-796.］

［3］ZHAO Yangang，TETSURO O.A general procedure for first／second-order reliability method（FORM／SORM）［J］.Structural Safety，1999，21（2）：95-112.

［4］ZENG Shengkui，ZHAO Tingdi，KANG Rui，et al.The system reliability design and analysis tutorials［M］.Beijing：Beijing University of Aeronautics and Astronautics Press，2001（in Chinese）.［曾声奎，赵廷第，康 锐，等.系统可靠性设计分析教程［M］.北京：北京航空航天大学出版社，2001.］

［5］SANDLER B Z.Probabilistic approach to mechanisms［M］.Amsterdam，the Netherands：Elsevier Science，1984.

［6］SUN Y，MA L，MORRIS J.A practical approach for reliability prediction of pipeline systems［J］.European Journal of Operational Research，2009，198（1）：210-214.

［7］CHIEN Y H.A number-dependent replacement policy for a system with continuous preventive maintenance and random lead times［J］.Applied Mathematical Modeling，2009，33（3）：1708-1718.

［8］XIAO Ningcong，HUANG Hongzhong，LI Yanfeng，et al.Multiple failure modes analysis and weighted risk priority number evaluation in FMEA［J］.Engineering Failure Analysis，2011，18（4）：1112-1170.

［9］JAYANT T，YANG K.Reliability function deployment（RFD）：a system approach［C］／／Proceedings of the 9th Symposium on QFD.AnnArbor，Mich.，USA：QFD Institute，1997：55-74.

［10］YANG K，KAPUR K C.Customer driven reliability：integration of QFD and robust design［C］／／Proceedings Annual Reliability and Maintainability Symposium.Washington，D.C.，USA：IEEE，1997：339-345.

［11］DU Lei，GAO Jianmin，CHEN Kun.Reliability deployment based on fault correlation analysis［J］.Computer Integrated Manufacturing Systems，2011，17（9）：1973-1780（in Chinese）.［杜 雷，高建民，陈 琨.基于故障相关性分析的可靠性配置研究［J］.计算机集成制造系统，2011，17（9）：1973-1780.］

［12］GEORGANTZAS N C，HESSEL M P.The intermediate structure of design for quality［J］.International Journal of Quality &Reliability Management，1995，12（6）：97-108.

［13］DER K A，ZHAN G Y，LI C C.Inverse reliability problem［J］.Journal of Engineering Mechanics，1994，120（5）：1154-1159.

［14］BRAGLIA M，FANTONI G，FROSOLINI M.The house of reliability［J］.International Journal of Quality &Reliability Management，2007，24（4）：420-439.

［15］CHENG Jin，ZHANG Jie，CAI C S，et al.A new approach for solving inverse reliability problems with implicit response functions［J］.Engineering Structures，2007，29（1）：71-79.

［16］ROBERTO M，ENRIQUE C，ALI S H .Solving the inverse reliability problem using decomposition techniques［J］.Structural Safety，2005，27（1）：1-23.

［17］SAIKAT S，MANOHA C S.Inverse reliability based structural design for system dependent critical earthquake loads［J］.Probabilistic Engineering Mechanics，2005，20（1）：19-31.

［18］LI Hong，RICARDO O F.An inverse reliability method and its application［J］.Structural Safety，1998，20（3）：257-270.

［19］LU Tingxiao，ZHENG Pengzhou，HE Guowei，et al.Reliability design and analysis［M］.Beijing：National Defence Industry Press，1997（in Chinese）.［陆廷孝，郑鹏洲，何国伟，等.可靠性设计与分析［M］.北京：国防工业出版社，1997.］