基于CAD 曲面模型的局部区域重构与特征化

何坤金，王 淋，陈正鸣+，赵宗星

（1.河海大学 物联网工程学院，江苏 常州 213022；2.疏浚技术教育部工程研究中心，江苏 常州 213022）

0 引言

特征造型技术是新一代CAD／CAM 集成系统的关键技术之一，是产品模型设计的核心。随着曲面造型技术的快速发展和广泛应用，产生了数量庞大、种类繁多的曲面模型，这些曲面模型普遍存在特征信息不完整、语义参数不充分等不足，难以有效进行编辑修改。如果每次完全从头开始设计新的曲面，对设计人员来说既耗时又需要丰富的经验和专业技能。因此，针对现存的大量曲面几何模型，研究曲面模型的特征化与编辑修改，减少设计工作的重复性，对提高产品设计的质量和效率具有重要意义。

近年来，国内外学者对曲面重构与重用进行了相关研究，并取得了一定成果。Biermann等［1］通过各种特征的“剪贴”操作进行曲面重构，增加了剪贴的交互性，但是带有复杂形状的特征在粘贴时可能会出现严重变形；赵伟等［2］提出一种基于层次B 样条的自由曲面特征重用算法，该算法能快速、有效地完成重用操作，并支持特征的缩放、旋转操作，但由于粘贴区域的变形是通过直接操作控制顶点的坐标来完成的，难以满足高精度的要求；高曙明等［3］提出基于Poisson方程的非均匀有理B 样条（Non-Uniform Rational B-Spline curve，NURBS）自由曲面特征重用方法，在保持重用特征微分属性不变的前提下生成单一连续的NURBS 曲面；Qin等［4］提出一种基于三角B 样条网格曲面重构点云数据的方法，有效地避免了曲面修补的复杂操作；Funkhouser等［5］提出以数据驱动的方式构建曲面模型的方法，该方法中目标模型的各组成部分（子特征）分别来自于现存的不同模型，体现了设计重用的思想。在逆向工程中，柯映林等［6］提出一种基于曲面变形的自由曲面特征重构方法，通过控制特征线和约束线实现了对重构曲面的编辑；邓建松等［7］提出一种利用隐性PHT-Spline表示法从大量的点中重构曲面模型；段黎明等［8］提出一种断层成像技术的三维CAD 模型重构方法，通过切片图像获取体数据，实现了标准模板库（Standard Template Library，STL）模型的重建。李际军等［9］提出基于草图线和轮廓线的模型曲面变形算法，实现了较直观的网格模型的变形。上述曲面重构与重用的各方法虽然都达到了设计者的要求，但是在重构曲面精度及其参数化设计上却鲜有研究。

目前，人们对规则曲面特征化的研究已经比较成熟，但对自由曲面的研究相对较少。随着自由曲面特征的应用日益广泛，自由曲面的特征化设计成为众多学者的研究热点。陆国栋等［10］提出基于三角网格实现三维服装的参数化设计，并结合实际应用将参数划分为多层；Van den Berg等［11-12］利用特征点定义特征线，通过特征线控制特征形状，提出一种基于曲线的自由曲面特征表示方法；Pernot等［13］提出完全自由曲面变形特征的概念，并且提供了特征生成和操作的方法和工具，随后把原有的工作扩展到参数化自由特征模板上［14］，但是所涉及的自由曲面特征主要局限于单一曲面；Nyirenda等15提出用数值参数和曲线参数描述自由曲面特征的方法，数值参数影响特征的整体形状，曲线参数影响特征的局部形状，但Nyirenda没有提出数值参数与曲线参数之间的映射关系；Langerak 等［16］提出一种采用三元组表示曲面特征的形式化方法，以NURBS的控制点作为曲面特征构建的基本元素，并在特征参数与控制点间直接建立映射关系，但映射关系过于复杂且难以实现。

笔者所在的工作组对自由曲面特征的参数化表示和分类方法做了部分研究，将自由曲面特征的参数和映射划分为“三层参数两级映射”结构［17］，有效地解决了特征参数之间复杂的映射关系问题，并为用户提供了曲面特征操作接口，以便用户通过高层参数直观地编辑修改自由曲面特征。本文在已有工作的基础上侧重于曲面重构过程中新生成曲面与源曲面的形状比较和修正，以及曲面特征化后的编辑修改。其中，采用Hausdorff距离作为描述两个曲面的形状相似度量［18］，以解决重构曲面的精度问题。

1 曲面特征化框架

曲面模型局部区域的特征化过程一般包括模型局部区域划分和选取、曲面重构和参数化和曲面特征类的生成等，流程如图1所示。

根据上述设计流程，基于曲面模型局部区域的特征化步骤如下：

步骤1 导入已有曲面模型，划分和选取模型中的局部区域，并确定其边界范围。

步骤2 对选取的曲面局部区域进行特征化，包括曲面重构和参数化两部分。

步骤3 将得到的曲面特征生成曲面特征类，并载入特征库。

其中，步骤1和步骤2为本文研究的主要内容。将以上流程所生成的曲面特征进行编辑修改或重用到新模型上，有效地降低了设计工作的重复性，提高了设计效率，并通过改变特征参数值实现了产品模型的多样化设计。

2 曲面特征化方法

在选取曲面模型局部区域并确定其边界范围后，所选取区域的特征化包括曲面重构和参数化两部分。首先，重构所选取的曲面区域，以便用户后期对曲面特征的编辑和修改操作；然后，对重构的曲面进行参数化设计。其中，重构曲面的精度对特征化的结果产生一定影响，本文着重研究重构曲面及其形状相似性比较。

2.1 局部区域的选取

在已有的曲面几何模型中选取局部区域，并确定其边界范围。用户所选取的区域一般是显著的、具有一定工程语义的区域，其边界范围由选定区域的几何信息或者用户绘制的封闭线确定，并通过系统提供的拉伸、旋转、扫略、覆盖和蒙皮等方式生成所需的局部区域。

图2a所示为某剃须刀的简化模型，侧面的凸状曲面可以作为用户选取的局部区域，其边界范围即为曲面的边界线所包含的区域，通过自动提取即可得到边界线信息；图2b所示为某茶壶盖模型，将顶部的把手作为用户所选取的区域，并根据其边界线和生成方式（旋转）确定边界范围。

2.2 曲面重构

自由曲面的重构主要分为三个步骤：①获取所选曲面的特征线草图；②选择一种合适的曲面生成方式，并生成新的曲面；③将新生成的曲面与源曲面进行形状比较。其中，新生成曲面与源曲面的形状比较为本节研究的重点。

2.2.1 获取曲面的特征线草图

在曲面特征造型中，点、线、面构成了曲面特征的几何元素。线位于点与面的中间层，特征信息比较集中，既没有点的繁琐也没有面的复杂，对其进行处理比对点和面更有优势。因此，特征线在曲面造型中不仅是造型的基本单元，还具有特征信息，决定了曲面特征形状的轮廓。

曲线的分类已有多种方式，依据曲线的自由度可分为退化二次曲线、非退化二次曲线、自由曲线和更复杂的自由曲线；依据曲线的生成方式可分为差值曲线、Bezier曲线、B 样条曲线和NURBS 曲线等；依据曲线的表示形式可分为显示、隐式和参数表示［19］；依据其造型功能可分为边界线和目标线［20］，本文根据特征线在曲面模型中的获取方式将特征线分为三类：

（1）曲面固有的特征线 即曲面已含有的曲线。曲面模型通常采用边界表示法，模型含有几何和拓扑信息，用户可以较容易地从曲面带有的线特征信息中直接提取。如图3b所示为手机振铃模型凸状曲面的边界线。

（2）利用算法识别的特征线 即在曲面较显著的位置上识别的曲线，如曲率较大的地方。本文侧重于通过曲面上的曲率最大值和连贯性获取此类特征线。其基本步骤如下：①在曲面上确定一个子区域；②在该区域内给定曲率的范围值，以曲率较大值为起点，通过曲率连贯性离散出曲率较大的点；③提取上述离散点中的关键点，通过插值法生成一曲线。图3c所示为在凸状曲面曲率较大的区域识别出的主特征线。

（3）交互绘制的特征线 即用户根据自己的意图在感兴趣的曲面上通过鼠标点击直观、快捷地绘制的曲线［21］。其基本步骤如下：①在选定的曲面上通过鼠标简单地点击，得到一系列初始点；②利用这些初始点，通过插值算法产生一初始曲线；③将产生的初始曲线投影到选定的曲面上，形成特征线，如图3d所示的辅特征线。

2.2.2 基于特征线草图的曲面重构

曲面形状一般由特征线草图和曲面生成方式共同决定，在特征线草图已经确定的情况下，生成方式将决定曲面的形状。在曲面重构过程中，用户需要根据源曲面的整体形状并结合自身的经验知识选择一种合适的曲面生成方式。在CAD 中，常见的曲面生成方式包括拉伸、旋转、扫略、覆盖、蒙皮、填充和放样等。图4列出了五种常见的曲面特征，其中图4a、图4b和图4c分别表示通过拉伸、旋转和扫略方式生成的拉伸曲面、旋转曲面和扫略曲面，本文侧重于采用覆盖和蒙皮的方式进行曲面重构。覆盖曲面的特征线草图必须包含一条封闭的边界线，在边界线限定的范围内可以包含通过算法识别的约束线或者用户自由绘制的约束线，然后采用覆盖的方式生成覆盖曲面，如图4d所示，边界线确定曲面的范围，内部的约束线决定曲面的基本形状。蒙皮曲面的特征线草图可以只包含多个约束线，这些约束线包括通过算法识别的或用户自由绘制的曲线，然后通过蒙皮方式生成蒙皮曲面，如图4e所示，包括3条截线，其截线按顺序依次组成，各截线决定其基本形状。

2.2.3 重构曲面与源曲面形状比较

为了描述两个曲面的形状相似性，本文利用Hausdorff测距法［22］对新生成的曲面进行误差比较。Hausdorff距离是描述两组点集之间相似程度的一种量度，其形式化定义为

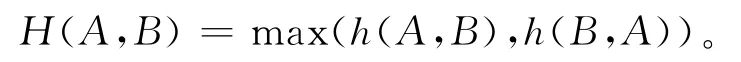
式中：

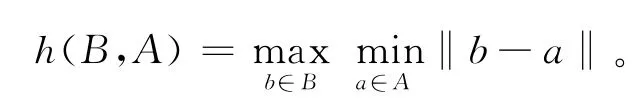
本文利用Hausdorff测距方法对重构曲面进行误差比较，在曲面S0（u，v）上等步长采样点集A=｛a1，…，an｝，在曲面S1（u，v）上等步长采样点集B=｛b1，…，bm｝，则S0和S1两曲面间的Hausdorff距离为H（A，B）。其基本步骤如下：

步骤1 在源曲面S0和重构曲面S1上分别以等u，v参数上取N×N个采样点。

步骤2 计算S0与S1之间的Hausdorff距离H（A，B）。

步骤3 当H（A，B）≤Dmax（Dmax为给定的误差阈值）时，认为重构曲面与源曲面基本一致。

步骤4 当H（A，B）＞Dmax时，认为重构曲面没有达到所需的精度，需要对曲面进行重新构建，并在误差较大的位置上添加约束线，重构新的曲面。

步骤5 重复执行步骤1～步骤4，直到H（A，B）满足所需的精度。

如图5所示的手机振铃模型上一凸块状的源曲面与重构曲面之间的形状比较，给定的误差阈值为0.25mm。图5a表示手机振铃简化模型，图5b中的重构曲面由源曲面的两条边界线和一条约束线组成的特征线草图通过蒙皮的方式生成，两曲面间的Hausdorff距离为0.324 25mm，大于所给定的误差阈值，需要重新构建。图5c中的特征草图又添加了6条辅助约束线，重新生成新的曲面，两曲面间的Hausdorff距离为0.166 73 mm，达到了所需的要求。

图6所示为一蝶状源曲面与重构曲面的形状比较，给定的误差阈值为0.25mm。图6a表示一蝶状自由曲面，图6b中的重构曲面由源曲面的两条边界线组成特征线草图并通过覆盖的方式生成，两曲面间的Hausdorff距离为0.270 55 mm，大于给定的阈值，没有达到所需的精度要求；在图6c源曲面中间添加了一条主约束线并重构曲面，Hausdorff距离为0.202 68mm，达到了所需要求；在图6d的源曲面两端再添加两条约束线重构曲面，Hausdorff距离为0.135 69mm，进一步提高了精度。

2.3 曲面的参数化

在曲面的参数化设计方面，将自由曲面特征的参数及其映射划分为三层参数两级映射的结构［14］，如图7所示。特征参数从高层到底层分为高层参数、中间层参数和底层参数，并在这三层参数间分别建立相关映射和约束关系。高层参数描述曲面特征的整体形状，中间层参数描述曲面特征线的形状，底层参数则描述曲面、曲线的特征点。该方法将中间层作为桥梁，实现高层与中间层、中间层与底层间的两级映射，有效解决了自由曲面特征参数之间复杂映射关系的问题，方便用户通过少量高层参数直观地编辑修改自由曲面特征。

本文主要采用基于CAD 模型的NURBS曲面进行参数化验证。图8所示为元宝模型的S型自由曲面特征进行参数化设计的过程。图8a为一元宝曲面模型，包含S型和半球型两个自由曲面特征，对其S型曲面的特征参数及其映射关系以三层参数两级映射的结构进行描述，并设置相应的参数，如图8b所示，其中：S表示曲面，C表示曲线，P表示特征点，L表示长度，W表示宽度，H表示高度等。

该自由曲面特征包括几何元素E、语义参数SP、参数之间的函数映射关系F、元素之间的约束关系R，即参数化定义为R｝。其中：几何元素包括E1=｛S1｝，E2=｛C1，C2｝，E3=｛P1，P2，P3，P4，P5，P0｝，E3中的六个元素表示C1，C2上的6个特征点；语义参数包括高层参数SP1=｛L，W，H｝，中间层参数SP2=｛L1，L2，H1，H2，a，b｝，底层参 数SP3=｛（x1，y1，z1），（x2，y2，z2），（x3，y3，z3），（x4，y4，z4），（x5，y5，z5），（x0，y0，z0）｝为E3中6个特征点的坐标；参数间的映射关系简单描述如下：F1=｛X→Y｜X∈P1，Y⊆P2｝表示高层参数和中间层参数之间的函数映射关系，F2=｛Y→Z｜Y∈P2，Z⊆P3｝表示中间层参数和底层参数之间的函数映射关系；元素之间的约束关系R1=｛L，W，H，H1，H2，L1，L2，a，b｝，用参数值表示自由曲面特征所定义参数的几何尺寸大小，R2=｛L=2×a，L=L1+L2，W=2×b，H=H1+H21，a＞0，0＜b≤a，H1＞0，H2＞0，L1＞0，L2＞0｝表示所定义参数之间的相互约束关系，R3=｛C1与C2相交于P1和P5｝表示特征曲线C1和C2之间的拓扑约束关系。

图8c为通过覆盖方式生成的S型曲面，并根据图8b进行的参数设置。图8d～图8f为分别改变其参数L，W和H后生成的曲面特征。

3 实例

本文所提方法在VC++2005和几何造型引擎ACIS R22平台上进行了实例测试，测试模型来自工业实际产品。下面以振铃模型和电动剃须刀模型为例说明局部区域的特征化。

图9为手机振铃模型的凸状曲面特征化过程：①导入的振铃简化模型，如图9a所示；②选取模型中的凸状曲面作为特征化的对象，如图9b的高亮部分所示；③获取凸状曲面的特征线草图，如图9c所示的特征线草图由两条封闭的边界线、一条主特征线和19条辅特征线组成；④利用已获取的特征线草图，由凸状曲面的整体形状选择覆盖的生成方式进行曲面重构，并通过Hausdorff测距法将新生成的曲面与源曲面进行形状比较，最终生成图9d所示的重构曲面；⑤图9e和图9f表示对重构曲面进行参数化后，分别改变其特征参数L（长度）和W（局部宽度）值所生成的曲面特征。

图10所示为电动剃须刀模型局部区域的特征化过程。首先，导入剃须刀的简化模型，如图10a所示；然后，选取模型侧面的凸状曲面，并获取其特征线草图，如图10b和图10c所示；再根据所选曲面的整体形状，选择覆盖方式生成新的曲面，并通过Hausdorff测距法得到所需精度的重构曲面，如图10d所示（下方凸状曲面）；最后，对重构曲面进行参数化，图10e和图10f表示分别改变特征参数L（长度）和H（高度）的值所生成的曲面特征。

本文方法的计算效率主要体现在特征线的提取、曲面的重构和形状精度比较上。其中，特征线提取的效率主要包括特征线的识别算法和曲线绘制部分（识别算法由n个离散点数决定，时间复杂性为O（n））；曲面重构的效率主要由曲面生成方式决定（不同生成方式的效率不同）；形状精度比较的效率主要由时间复杂性决定（一般选择n个离散点，时间复杂性为O（n2））。实验表明，本文所提方法是一种有效的曲面模型局部区域的重构与特征化方法，该方法能够使用户方便、快捷地对曲面模型的局部区域进行特征化设计，并通过高层参数进行直观的编辑修改，从而提高产品设计的效率。

4 结束语

本文提出一种基于特征线的曲面模型局部区域重构与特征化方法，该方法对产品模型的局部区域进行参数化并生成曲面特征，有效地解决了曲面模型局部曲面区域的编辑修改问题。针对重构曲面的形状精度，引入Hausdorff距离作为重构曲面与源曲面的相似性度量，并通过添加相关的约束线减小两曲面间的Hausdorff距离，从而提高了重构曲面的精度。但是，在添加约束线的过程中还无法做到完全自动添加，该问题有待在今后的工作中进一步研究和完善。

［1］BIERMANN H，MARTIN I，BERNARDINI F，et al.Cutand-paste editing of multiresolution surfaces［C］／／Proceedings of ACM SIGGRAPH 2002.New York，N.Y.，USA：ACM，2002，21（3）：312-321.

［2］ZHAO Wei，GAO Shuming.Freeform feature reuse based on hierarchical B-spline［J］.Journal of Computer Aided Design &Computer Graphics，2008，20（1）：6-12（in Chinese）.［赵 伟，高曙明.基于层次B样条的自由形状特征重用［J］.计算机辅助设计与图形学学报，2008，20（1）：6-12.］

［3］ZHAO Wei，GAO Shuming，LIU Yusheng，et al.Poisson based reuse of freeform features with NURBS representation［J］.Computers in Industry，2009，60（1）：64-74.

［4］HE Ying，QIN Hong.Surface reconstruction with triangular B-splines［C］／／Proceedings of GMP 2004.Washington，D.C.，USA：IEEE，2004：279-290.

［5］FUNKHOUSER T，KAZHDAN M，SHILANE P，et al.Modeling by example［J］.SIGGRAPH，2004，23（3）：652-663.

［6］WANG Qing，LI Jianxiong，KE Yinglin.Deformation-based freeform feature reconstruction in reverse engineering［J］.Journal of Zhejiang University Science A，2008，9（9）：1214-1228.

［7］WANG Jun，YANG Zhouwang，JIN Liangbing，et al.Parallel and adaptive surface reconstruction based on implicit PHTsplines［J］.Computer Aided Geometric Design，2011，28（8）：463-474.

［8］DUAN Liming，LIU Yuanbao，WU Zhifang，et al.Method of reconstructing 3D CAD model based on industrial computed tomography［J］.Computer Integrated Manufacturing Systems，2009，15（3）：479-486（in Chinese）.［段黎明，刘元宝，吴志芳，等.基于工业计算机断层成像技术的三维CAD 模型重构方法［J］.计算机集成制造系统，2009，15（3）：479-486.］

［9］CHEN Baoyu，LI Jijun.Mesh deformation method based on sketch［J］.Computer Integrated Manufacturing Systems，2010，16（6）：1168-1174（in Chinese）.［陈保宇，李际军.基于草图的网格曲面变形算法［J］.计算机集成制造系统，2010，16（6）：1168-1174.］

［10］CHEN Long，WANG Jin，LU Guodong.3Dgarment design with parameterization methods［J］.Journal of Computer Aided Design &Computer Graphics，2011，23（9）：1504-1512（in Chinese）.［陈 龙，王 进，陆国栋.三维服装参数化设计技术［J］.计算机 辅助设 计与图 形学学 报，2011，23（9）：1504-1512.］

［11］VAN DEN BERG E，VAN DER MEIDEN H A，BRONSVOORT W F.Specification of freeform features［C］／／Proceedings of the 8th ACM symposium on Solid modeling and applications.New York，N.Y.，USA：ACM，2003：56-64.

［12］VAN DEN BERG E.Free form feature modeling and validity maintenance［D］.Delft，the Netherlands：Delft University of Technology，2007.

［13］PERNOT J P，FALCIDIENO B，GIANNINI F，et al.Fully free-form deformation features for aesthetic shape design［J］.Journal of Engineering Design，2005，16（2）：115-133.

［14］PERNOT J P，GIANNINI F，FALCIDIENO B，et al.Parameterised free-form feature templates［C］／／Proceedings of IEEE International Conference on Shape Modeling and Applications.Washington，D.C.，USA：IEEE，2009：140-147.

［15］NYIRENDA P J，BRONSYOORT W F.Numeric and curve parameters for freeform surface feature models［J］.Computer-Aided Design，2008，40（8）：839-851.

［16］LANGERAK T R，VERGEEST J S M.A new framework for the definition and recognition of free form features［J］.Journal of Engineering Design，2007，18（5）：489-504.

［17］HE Kunjin，CHEN Zhengming，ZHAO Lihua.A new method for classification and parametric representation of freeform surface feature［J］.International Journal of Advanced Manufacturing Technology，2011，57（1-4）：271-283.

［18］LANGERAK T R.Local parameterization of freeform shapes using freeform feature recognition［J］.Computer-Aided Design，2010，42（8）：682-692.

［19］SUN Jiaguang.Computer graphics［M］.3rd ed.Beijing：Tsinghua University Press，2005：301-333（in Chinese）.［孙 家广.计算机图形学［M］.3 版.北京：清华大学出版社，2005：301-333.］

［20］PERNOT J P，GUILLET S，LEON J C.A shape deformation tool to model character lines in the early design phases［C］／／Proceedings of the 8th ACM Symposium on Solid Modeling and Applications.New York，N.Y.，USA：ACM，2003：165-172.

［21］DEKKERS E，KOBBELT L，PAWLICKI R，et al.A sketching interface for feature curve recovery of free-form surfaces［J］.Computer-Aided Design，2011，43（7）：771-780.

［22］HOPPE H，DEROSE T，DUCHAMP T，et al.Surface reconstruction from unorganized points［C］／／Proceedings of ACM SIGGRAPH 1992.New York，N.Y.，USA：ACM，1992：71-78.