基于并联机构调姿的大部件支撑点优选

张洪双，王 青，柯映林，蒋君侠

（1.浙江大学 流体传动及控制国家重点实验室，浙江 杭州 310027；2.河海大学 机电工程学院，江苏 常州 213022）

0 引言

在造船、飞机等大型运载设备的模块化分段对接装配以及机翼大部件装配后的精加工等工艺过程中［1-2］，需要采用先进的数字化调姿系统实现部件的调姿和定位。目前国内外广泛采用一种数字化、高精度的并联机构形式的定位调姿装置，对大部件进行姿态调整及支撑［3］。

并联机构是一种闭环运动链机构，它通过几个独立的运动链将底座和终端执行器连接在一起。由于具有高精度、高刚度等优点，国内外对其展开了大量研究，并成功应用到运动模拟器、机器人终端和部件调姿等环境中。目前，几大航空制造企业使用的数字化并联机构大多采用n-PPPS（n个prismaticprismatic-prismatic-spherical pair）分支垂直布置在一个公共平台上的结构形式［4］。文献［5］介绍了部分耦合的并联机构，并对现有的并联机构进行分析和扩展，详细介绍了3-RPPS（R-Rotary pair）型机构的分析方法，并对扩展的并联机构进行了分类；文献［6］介绍了由8个驱动机构驱动的PPPS并联机构，该机构的底部有4个分支，两侧面各有2个分支，8个分支均为主动驱动，主要用于地震监测；文献［7］介绍了一种新型的3-PPPS并联机构，3个分支机构分别位于3个相互垂直的平面，每个分支中有2个主动驱动的关节，并分析了该机构的非奇异空间，上述结构和国外飞机制造企业所使用的PPPS型并联机构在整体布置方式上均有较大的差别。

基于并联机构形式的定位调姿装置既是飞机部件姿态调整的执行机构，也是装配对接过程的工装夹具，因此其分析需要同时涉及两方面内容。文献［8-10］关注并联机构的机构雅克比矩阵，并通过机构雅克比矩阵构建相应的性能评价指标；文献［11-12］对并联机构进行优化分析，重点关注各分支长度的优化问题，未涉及终端部件连接位置点的分析。关于夹具定位性的文献较多［13-14］，这类文献通过描述夹具偏差和零件偏差之间关系的定位雅克比矩阵，对夹具定位方案的稳定性问题进行分析，但分析过程主要针对零件上定位点的曲面方程，未涉及夹具实体。

本文针对基于3-PPPS并联机构形式的大部件定位调姿装置［15］，建立了装置分支机构的矢量图形，求取了装置的机构雅克比矩阵，构建了灵活度、承载力和刚度等性能指标，并分析了装置的定位雅克比矩阵，构建了装置的支撑稳定性指标，最后对部件上可选的支撑点的位置进行了分析，得到了各指标综合最优的支撑点位置，为选择基于并联机构形式的部件定位调姿装置的支撑点提供了一种参考。

1 定位调姿装置分析

1.1 大部件定位调姿装置结构

大部件定位调姿装置主要包括工作台、三坐标数控定位器和激光跟踪仪等，如图1所示。数控定位器在3 个坐标方向的运动为平移—平移—平移（PPP）形式，每个移动关节通过电机驱动滚珠丝杆进行传动，其中：x和y移动方向平行于工作台坐标系，z方向垂直于工作台。大部件通过万向球铰式真空吸附结构或者是带有球头的工艺接头和定位器的终端执行器连接，因此每个定位器连接可以看作一个PPPS型的分支机构。

大部件加工或对接装配时需要通过定位调姿装置使部件处于某个理想位姿，其位置和姿态通过激光跟踪仪的测量数据进行评价。根据部件的结构尺寸特点，三角形的大部件（如机翼等）通常采用3个数控定位器支撑的方式定位，通过3个定位器的协同运动实现部件的姿态调整，达到理想位姿后实现对接装配，或者通过专用机床对大部件的交点孔、面进行加工。根据大部件定位调姿装置的结构特点建立其运动学模型，图2所示为大部件调姿装置的并联机构形式的整体结构简图。

为了方便分析，建立如下坐标系统：其中坐标系o-xyz固定在工作台上，坐标系o-uvw固定在大部件的惯性主轴上，则大部件的位姿可以通过位置矢量r和角度变化矩阵来表示，用一个6维列矢量可以表示为

这里，r=［px，py，pz］表示坐标系o-uvw相对于坐标系o-xyz的位置。旋转矩阵通过滚动角θ（roll）、俯仰角φ（pitch）和偏转角ψ（yaw）来定义，三个角度分别对应x，y和z三个轴的旋转，则旋转矩阵R表示为（角度设定法是两个坐标系间作三次连续转动来规定姿态的方法）

式中：c表示cos，s表示sin。

1.2 大部件的支撑定位点

大部件通常采用框架式结构，其支撑定位点需选择在部件框架的交点处，且支撑定位时应保证部件重心落在由3个支撑点构成的三角形内部。大部件上框架的交点较多，每个数控定位器对应的位置均有多个支撑定位点可供选择。图3所示为某大部件模型，粗实线表示部件的外形（工作台的投影平面内），细实线表示部件内部的框架位置，细实线交点为框架的交点。3个数控定位器对应大部件上3个可选的定位区域：定位器1对应大部件上A区域内的框架交点；定位器2 对应B区域内的框架交点；定位器3对应C区域内的框架交点。

2 机构雅克比矩阵

2.1 位置分析

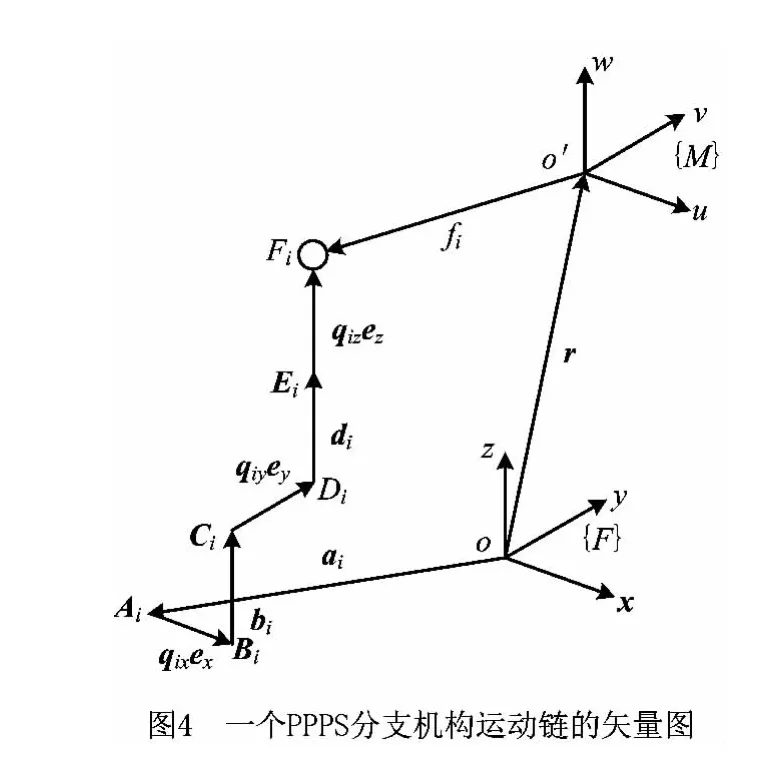
根据调姿装置的结构及平台和部件之间的位置关系，建立如图4所示的运动链矢量图，驱动链的闭环位置方程表示为

式中：r表示OO′矢量，fi为支撑点位置到部件重心的矢量，ai为平台中心到定位器中心的矢量，qix为定位器x方向的关节变量，qiy为定位器y方向的关节变量，qiz为定位器z方向的关节变量，ex，y，z为沿着丝杆的 单位矢 量，bi为BiCi矢 量，di为DiEi矢 量，bi和di分别表示各关节上的距离差值。根据并联机构解耦的概念［5］，可知其位置逆解为

式中下标x表示在x方向的投影。

1.3 分支机构速度分析

将方程对时间t求导，得到速度方程

式中：v为大部件移动的线速度，ω为大部件转动的角速度。

对式（3）两端分别点乘ex，ey和ez，合并后可得定位器沿各轴向的速度

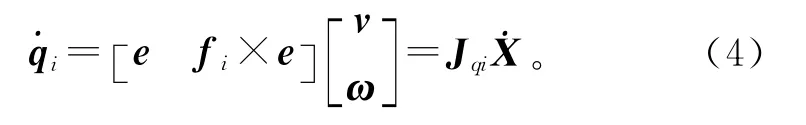
式中：

为平台运动矢量和定位器i沿各轴的平移速度矢量之间的雅可比矩阵，则多个分支机构的综合描述为

为了分析的一致性，引用机器人雅可比矩阵，该矩阵是指从关节空间到操作空间运动速度传递的广义传动比，将式（5）改写为

式中JP为并联机构的机构雅克比矩阵。由式（4）～式（6）可见，机构雅可比矩阵依赖于部件在操作空间的形位，是依赖于关节变量˙q的线性变换矩阵，其行数等于机构在操作空间的维数，列数等于关节数，因此雅可比矩阵并不是一个方阵，其逆矩阵是一个广义逆矩阵。

3 定位调姿装置的性能评价

3.1 灵巧度性能评价

在评价并联机构传动性能时，可构建的灵巧度评价指标有条件数k、最小正奇值σmin等。机构设计时应使条件数最小、最小正奇值最大。机构分析中常用最小条件数来分析机构的各向同性指标，当条件数达到最小值1时，机构为各向同性。根据文献［8］，输入速度偏差δ˙q和平台的速度偏差δ˙X之间有下列关系：

3.2 承载力性能评价

承载力决定了机构的工作负荷能力，是机构的重要性能指标之一。作用在机构末端的广义力与机构的雅克比矩阵有直接关系，定义机构驱动部件的输入力矩为f，作用在机构末端大部件平台的力和力矩矢量为F，则根据虚功原理可得

式中G为力雅可比矩阵。根据机构学中运动传递和力传递之间的对偶关系，存在［9］

将机构的承载能力指标定义为输入驱动力矢量f的模为单位1时输出力和力矩矢量的模极值。当‖f‖=1时，承载力极值‖Fmax‖为矩阵GTG的最大、最小特征值的开方，即

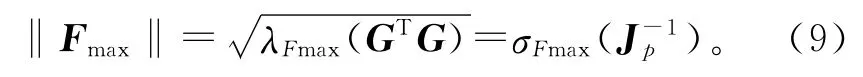
式中λFmax（GTG）为矩阵GTG的最大特征值的开方；）为矩阵的最大奇异值。

3.3 刚度性能分析

当部件放置在调姿装置上时，部件中心会发生变形，该变形与装置的刚度矩阵和外力的大小方向有关，当外力矢量的模为1时，可以求出部件中心变形量的最大值，变形量最大值即为并联机构的刚度性能指标，则并联机构形式的平台中心的变形D与外界作用力矢f之间的关系为

式中C为刚度矩阵。由文献［10］可知，并联机构的刚度矩阵可以写作

式中：KJ=diag［K1，K2，…，Kn］是并联机构的刚度矩阵，Ki表示每个分支的刚度，因为每个分支的结构均相同，所以驱动件刚度可以认为是相等的，并且等于单位1。

根据拉格朗日方程原理［10］可得，位置变形的最大值Dmax为

式中：λDmax（CTC）为矩阵CTC的最大特征值，σDmax（J·JT）为矩阵J·JT的最大奇异值。

3.5 全条件性能指标

上述各指标是雅克比矩阵的函数，而雅克比矩阵不是常数矩阵，依赖于机构的位形。各个指标均为局部点的性能指标，其值随机构位形的变化而变化。为了评价并联机构的总体性能，需要采用全条件性能指标（Global Conditioning Index，GCI）。GCI表示为

式中：W为并联机构的工作空间，ζ表示各性能指标，在灵巧度、承载能力和刚度评价中分别表示灵巧度指标k、承载力指标‖Fmax‖ 和刚度指标‖Dmax‖。式（13）的数学含义为各性能指标在可达工作空间上的平均值，计算时可采用网格搜索法对并联机构在可达空间内每一点的数值求解后进行平均化处理。

4 定位雅克比矩阵及定位稳定性

如图5所示，对于某任意的三维零部件的定位支撑方式，其定位雅克比矩阵的形式为

在三维空间中，

位于空间中的一个零件共有6个自由度，通常，若使零件在空间中处于一个稳定的状态，则需要约束零件的6个自由度，JL的秩等于调姿装置所约束的自由度数目。零件的定位方案中被约束零件的空间稳定性称为该夹具定位方案的几何稳定性［11-12］，夹具的稳定性参数的计算方法为

由式（15）可知，即使零件被约束的自由度数相同，定位的几何稳定性也有很大的差别。

5 各指标的综合优化

由上述分析可知，基于并联机构形式的定位调姿装置的性能指标取决于支撑点和部件重心之间的位置关系，而夹具稳定性指标取决于支撑点所在位置的曲面方程和支撑点位置，因此选定支撑点后上述指标就会确定，在多种支撑点的不同组合形式下，可以找到各指标的最优值，合理选择支撑点，从而得到各指标的综合优化值。

在定位调姿装置的性能指标中，灵巧度指标k越小越好，承载力指标‖Fmax‖越大越好，刚度指标‖Dmax‖越小越好，定位稳定性指标ω越大越好。各指标中既包括最大值问题，也包括最小值问题，则指标的综合优化求解属于多目标混合优化问题，优化模型为

式中：F′（x）=［f1（x），…，fr（x）］T，F″（x）=［fr+1（x），…，fn（x）］T；解决这类问题可用分目标乘除法，将模型中的各分目标进行相乘和相除处理后在可行域进行求解。由于各指标数值相差较大，对各指标进行归一化处理，即对各指标进行权处理：

式中Wi为权系数，并有

根据工程需求调整各指标的权重比例，以更好地满足机构的使用要求。由式（16）求解的最优解，是使位于分子的各目标函数尽可能小、位于分母的各目标函数尽可能大的综合性能指标。

6 算例分析

某大部件的支撑点位置如图3所示，部件重心点坐标为（2 300，8 600，1 800），部件坐标系和部件重心重合。由式（4）可知，机构雅克比矩阵值主要取决于球铰中心点到大部件中心点的矢量fi，对大部件进行位置调整时，fi不变化，因此机构雅克比矩阵值与大部件的位置变化没有关系。

由式（14）可知，定位雅克比矩阵主要取决于支撑点位置坐标及该位置处的部件曲面方程。为简化分析，假设部件的下表面为一平面，则在坐标系ouvw中，式（14）可近似写为

可见定位雅克比矩阵主要取决于定位点在xy平面的坐标值。

下面分析大部件绕x，y和z轴进行0～10°范围姿态调整时各性能指标的变化。选择支撑点A1（1 350，8 120，1 750），B3（2 986，8 120，1 750），C9（2 986，9 958，1 750）的组合，按照式（8）、式（9）、式（12）和式（15）求取机构的各性能指标，可以得到如图6所示的性能指标曲线（各指标数值差别较大，为了清晰地描述图形，纵坐标未采用统一比例）。由图6可见，灵巧度、承载力和刚度性能指标不随姿态的变化而变化，但稳定性指标随着姿态的改变而变化，且随着旋转角的增大而减小，因此后续分析时均以部件绕x，y和z轴旋转10°的状态进行分析。由图6中的数值可见，基于3-PPPS型的大部件定位调姿机构是一种调姿灵巧度较差、承载力高、稳定性较高和部件变形较小的一种并行机构，能够满足机翼这类大部件对调姿速度要求不高、但对承载和精度要求较高的部件调姿和精加工需求。

为了定性分析支撑点的位置变化对性能参数和支撑稳定性的影响，选取A1，B3和C9点作为初始位置，使支撑点坐标在x和y方向等距移动，得到如图7所示的各性能指标和稳定性指标的变化曲线，为了便于表达，各性能指标进行了均一化处理。由图7可见，支撑点靠近重心时：条件数减小，即机构的调姿灵巧度增加，各向同性增强；承载力指标下降，说明在驱动关节输入同样大小的力，机构执行端的输出力下降；刚度指标下降，说明部件的中心变形量下降；稳定性指标下降，说明支撑稳定性下降。从综合指数来看，选择远离重心点的支撑位置时可以获得较好的综合性能指标。

7 结束语

根据上述分析，可以得到以下结论：

（1）基于3-PPPS并联机构的大部件姿态调节装置能满足大部件的调姿需求。

（2）该定位调姿机构的灵巧度、刚度和承载力性能指标与支撑点的选择有关，与大部件的位姿无关。

（3）不同支撑点的组合可以得到不同的性能指标。

（4）稳定性指标既和支撑点的选择有关，也于大部件的姿态有关。

下一步将重点关注在明确了机翼支撑点后，分析和研究支撑多个机翼时定位器的工作行程优化问题，以及在多点柔性支撑状态下机翼的加工稳定性问题。

［1］LIU Chuhui，KE Yinglin.Joint measuring and evaluating technology for final assembly of aircraft wing and fuselage［J］.Journal of Zhejiang University：Engineering Science，2011，45（2）：201-208（in Chinese）.［刘楚辉，柯映林.飞机翼身对接装配中的接头测量与评价技术［J］.浙江大学学报：工学版，2011，45（2）：201-208.］

［2］JING Fengshui，TAN Min.Posture aligning and merging system for boat blocks—realization of coordinated manipulation with multi-robot system［J］.Acta Automatica Sinca，2002，28（5）：708-714（in Chinese）.［景奉水，谭 民.船体分段位姿找正对接系统——一个多机器人协调操作系统的实现［J］.自动化学报，2002，28（5）：708-714.］

［3］ZOU Jihua，LIU Zhicun，FAN Yuqing.Large-size airplane parts digital assembly technology［J］.Computer Integrated Manufacturing Systems，2007，13（7）：1367-1373（in Chinese）.［邹冀华.刘志存.范玉青.大型飞机部件数字化对接装配技术研究［J］.计算机集成制造系统，2007，13（7）：1367-1373.］

［4］QIU Baogui，JIANG Junxia，BI Yunbo，et al.Posture alignment and joining test system for large aircraft fuselage［J］.Acta Aeronautica et Astronautica Sinica，2011，32（5）：908-919（in Chinese）.［邱宝贵，蒋君侠，毕运波，等.大型飞机机身调姿与对接试验系统［J］.航空学报，2011，32（5）：908-919.］

［5］JIN Y，CHEN I，YANG G.Kinematics design of a family of 6-DOF partially decoupled parallel manipulators［J］.Mechanism and Machine Theory，2009，44（5）：912-922.

［6］ZHAO Y，GAO F.Dynamic formulation and performance evaluation of the redundant parallel manipulator［J］.Robotics and Computer-Integrated Manufacturing，2009，25（4／5）：770-781.

［7］CARO S，WENGER P，CHABLAT D.Non-singular assembly mode changing trajectories of a 6-DOF parallel robot［C］／／Proceedings of the ASME 2012International Design Engineering Technical Conferences &Computers and Information in Engineering Conference.New York，N.Y.，USA：ASME，2012.

［8］LIU Su.Design of 1T3Rparallel robot and development of the experimental equipment［D］.Chongqing：Chongqing University，2006（in Chinese）.［刘 溯.1T3R 并联机器人设计及其实验装置研制［D］.重庆：重庆大学，2006.］

［9］ZHANG Lijie，LIU Ying，HUANG Zhen.Analysis of perfoemances of planar 2-DOF parallel manipulator with actuation redundancy［J］.Chinese Journal of Mechanical Engineering，2006，42（7）：181-186（in Chinese）.［张立杰，刘 颖，黄 真.平面2 自由度驱动冗余并联机器人的性能分析［J］.机械工程学报，2006，42（7）：181-186.］

［10］ZHANG Yanwei，CUI Guohua，SUN Zhenjun，et al.Kinematic performance analysis of 3-SPSS spatial rotation parallel mechanism［J］.Transactions of the Chinese society for Agricultural Machinery，2010，43（4）：199-203（in Chinese）.［张艳伟，崔国华，孙振军，等.空间转动3-SPS-S 型并联机构奇异位形研究［J］.农业机械学报，2010，43（4）：199-203.］

［11］ZHAO Xinhua，ZHANG Wei.Parameter optimization of the3-RTT parallel manipulator based on the conditioning index［J］.China Mechanical Engineering，2005，15（21）：1903-1905（in Chinese）.［赵新华，张 威.基于条件数的3-RTT并联机器人参数优化［J］.中国机械工程，2005，15（21）：1903-1905.］

［12］ZHANG Lijie.Performance analysis and dimension optimization of 2-DOF parallel manipulators［D］.Qinhuangdao：Yanshan University，2006（in Chinese）.［张立杰.两自由度并联机器人的性能分析及尺寸优化［D］.秦皇岛：燕山大学，2006.］

［13］JIANG Ang，FAN Qinglin，ZHENG Cheng，et al.Stability evaluation of fixture locating layout and research in locatorsearching algorithm［J］.Journal of Shanghai Jiaotong University，2010，44（4）：484-488（in Chinese）.［姜 昂，范清林，郑丞，等.夹具定位方案稳定性评价及定位点搜索算法［J］.上海交通大学学报，2010，44（4）：484-488.］

［14］XIONG C，XIONG Y.Stability index and contact configuration planning for multifingered grasp［J］.Journal of Robotic System，1998，15：183-190.

［15］GUO Zhimin，JIANG Junxia，KE Yinglin.Static stiffness of three-axis actuators based posture alignment system for large aircraft components［J］.Journal of Zhejiang University：Engineering Science，2010，44（11）：2077-2083（in Chinese）.［郭志敏，蒋君侠，柯映林.基于定位器的飞机大部件调姿系统静刚度［J］.浙江大学学报：工学版，2010，44（11）：2077-2083.］