散乱数据点的齿面重建及局部特征优化

胡伟端，黄筱调，2，张 虎，郭二廓

（1.南京工业大学 机械与动力工程学院，江苏 南京 210009；2.江苏省工业装备数字制造及控制技术重点实验室，江苏 南京 210009）

0 引言

齿轮是机械装备中主要的传动部件，精度是其性能的重要指标，齿轮修形技术［1］是高精度齿轮传动设计和制造的关键技术，基于目标的修形理论需要确定齿面修形的部位和修形量，建立拓扑修形的数字化齿面，通过实际修形齿形与目标修形齿形之间的误差对机床运动轴进行控制。对实际齿面进行测量可以获得齿面上大量离散的点云数据，对处理后的点云数据进行曲面重建可以建立数字化齿面模型。文献［2］由离散点云数据，经过处理后导入三维造型软件，生成锥齿轮三维实体模型，但采用该方法得到的齿面精度有限。Geetika Tewari等3采用双周期全局参量法对5 044个齿轮点数据进行重建，该方法不需要对数据进行分块，但由于采用全局变量，需要大量的数据结构且属于粗重建；Wang Yutao等［4］采用自动估计局部自适应参数的方法对扫描后的齿轮点数据进行重建，该方法不需要原始点云法向量信息且具有一定的健壮性，但在估计每个点的特征系数时需要大量的计算时间，且并没有对齿轮重建后的精度进行分析。

细分是对初始网格重复运用新顶点生成规则和顶点间的连接关系，细化出可收敛于光滑连续曲面的曲面重建技术。Loop［5］的方法是一种经典的细分方法，在此基础上，李桂清等［6］实现了一个基于带尖锐特征的Loop细分曲面的三角网格拟合系统；白杰等［7］用带折痕的不同层次的Loop细分网格等距面作为不同加工工序的加工模型，让细分技术更贴近应用。但细分技术应用于齿面重建的研究较少，邢元［8］运用细分技术重建出螺旋锥齿轮齿面，通过造型软件对齿面的几何特征进行提取，并没有对齿面局部的尖锐特征，如折痕、尖刺和角等进行相应研究。本文就上述研究中对齿面重建时的缺陷和漏洞作了进一步研究，提出重建齿面的新方法，并通过实验分析重建齿面的质量。

1 带特征的Loop齿面

1.1 特征的分类

文献［9-10］中给出了刺点、角点和折痕等尖锐特征的定义，定义如下：

（1）折痕（crease）曲面上一阶光滑曲线，曲面沿该曲线为C0连续的，而在其附近至少是C1连续的。

（2）角点（corner）两条或两条以上边界边交汇点、边界与折痕的交汇点、三条或更多的折痕的公共交汇点。

（3）刺点（dart）曲面内部顶点，折痕在此处终止，曲面在顶点至少是C1连续的。

（4）尖点（cusp）与锥点类似，其极限切矢量为一维的，曲面在该点是C0连续的。

此外，特征还应包括网格的边界边和边界上的边界点。

1.2 细分规则

（1）内部光滑边点（点）的细分规则

1）V-顶点 内部光滑点V的1-领域相连的顶点为V1，V2，…，Vk，其中n为光滑点的价，经过一次细分后，相应的V-顶点为

2）E-边点 内部光滑边的两个顶点为V0和V1，该边两邻接三角形面为（V0，V1，V2），（V0，V1，V3），则E-边点为

（2）刺点的细分规则

刺点是折痕的端点，与曲面光滑过渡，而且与刺点相连的边有且只有一条是折痕边，其余为曲面内部光滑边，刺点的细分规则与内部光滑点的细分规则相同。

（3）折痕边点（点）、边界边点（点）的细分规则

1）V-顶点 设V0为折痕点、边界点，V1和Vk是与V0直接相连的两特征点，则相应的V-顶点为

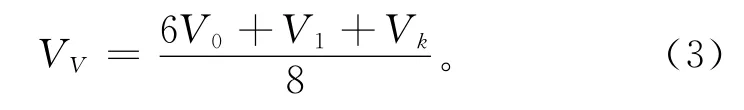
2）E-边点 假设特征边的两端点为V0和Vk，不同情况下的折痕点计算公式如下：

当顶点V0和Vk都是正则折痕点或者都是奇异折痕点时，E-边点为

当顶点Vk是正则顶点，V0是奇异顶点时，

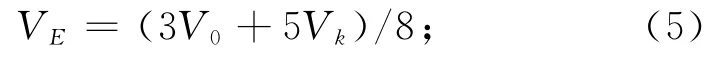
当顶点V0是正则顶点，Vk是奇异顶点时，

（4）角点、尖点的细分规则

角点和尖点在细分过程中的位置不变，即

1.3 特征点的极限位置

1.3.1 内部光滑点的极限位置

将式（1）和式（2）写为矩阵形式：

式（8）中（n+1）×（n+1）方阵称作为Vk局部细分矩阵Mn+1，化简矩阵Mn+1得

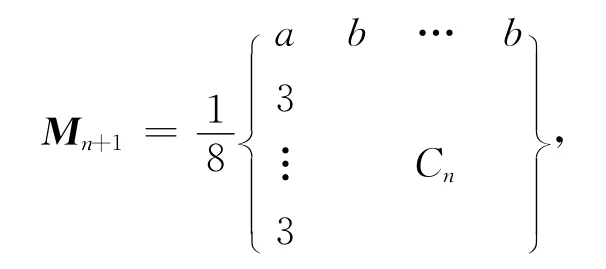
该式的特征多项式为

式中：a=8-8nβn，b=8βn；Cn是n维数组｛3，1，0，…，0，1｝的循环矩阵，对循环矩阵Cn进行傅里叶分析，可以求出Cn的特征值为

通过对式（9）和式（10）的特征值进行分析，可得Mn+1的最大特征值为λ0=1，对应的左特征向量l0=，其中w=3／（8β）。又因为矩阵Mn+1不是亏损的，且具有仿射不变性，可以得到顶点V的极限位置：

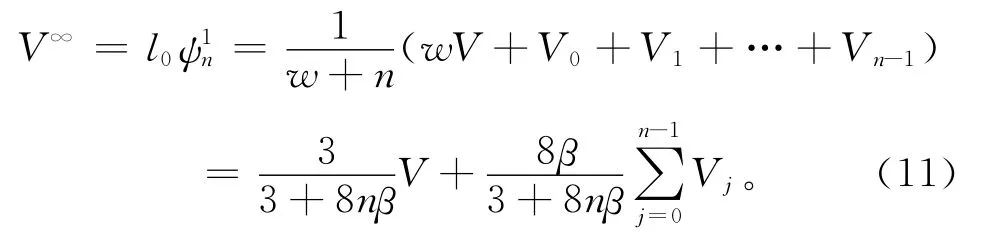
1.3.2 折痕、边界点、角点、尖点的极限位置

由式（3）～式（7）细分规则，根据上述求光滑点的方法同理可以求出其他顶点的极限位置，表1列出了折痕点、边界点、角点和尖点的极限位置。

表1 特征点的极限位置

2 大量散乱点数据齿面细分重建原理

本文算法是以齿面上大量散乱点的原始数据｛pi｝为输入量，通过如图1所示的大量散乱点数据齿面细分重建算法原理说明图重建流程，最终生成细分齿面。

2.1 建立初始网格

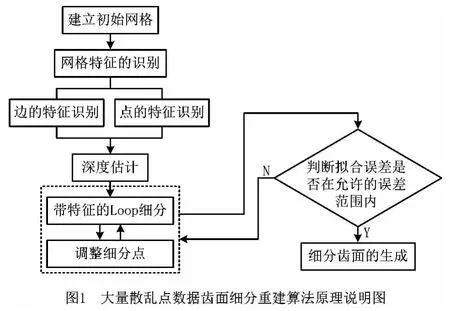
原有的相关文献通过建立形状简单的初始网格，不断对网格控制顶点进行循环逼近修正，每次在修正控制顶点后又采用拉普拉斯算子对修正后的网格进行网格优化，直到总体平均误差小于给定的拟合精度，结束循环修正。为了避免上述建立初始网格的复杂过程，本文提出一种空间三角网格螺旋增长重建出齿面粗模型的算法。

螺旋增长算法流程如下：

（1）输入齿面大量散乱点的原始数据｛pi｝，通过设定具有上下限的阈值PDIST去除冗余点，计算法矢保留特征点，噪声点的剔除，对原始数据｛pi｝进行预处理，得到简化后的数据｛p′i｝。

（2）采用极坐标法选取初始顶点p′1，通过距离尽量最短的原则找出p′2和p′3，构造出初始三角形Δp′1p′2p′3。

（3）以初始三角形Δp′1p′2p′3为基础，根据最长边限定原则（最长边不超过kPDIST，k为限制系数）、最小内角MIA限定原则（不得小于30°，主要避免狭长三角形的产生）、二面角DA最小原则（避免三角形重叠和保证生成的三角网格中具有公共边的三角形不超过2个，即生成的三角网格是二流形网格），不断从简化后的数据｛p′i｝中找出扩展点。其中扩展点分为邻接边的端点和首次成为扩展点的点（外点），算法参数取值如表2所示。

表2 算法参数的取值

（4）在每次寻找扩展点时，要对当前网格在点链表中对应的点进行加锁和解锁操作，先对网格在点链表对应的点进行加锁，再对当前边的上一边的起点和下一边的终点进行解锁，并对已成为扩展点的点进行标记。

（5）直到｛p′i｝中无可用的点，结束算法。

2.2 识别网格特征

2.2.1 边的特征识别

对边链表进行查找，由于根据上述算法构造出的网格为二维流形网格，当边只属于一个三角面时，可判断此边为边界边；对折痕边的判断可采用二面角是否超过给定的阈值（阈值由实验测得）进行判断，并对边界边和折痕边分别进行标记。

2.2.2 点的特征识别

对点链表进行循环，通过点的价数判断与该点直接相连的边是否已作标记，设标记的个数为n，根据1.1节特征的分类：n=0时，该点为内部正常点；n=1时，该点为刺点；n=2时，该点为折痕点或边界点；两条边界边交点或边界边与折痕交点为角点；1-领域三角面与2-领域邻接三角面的二面角均超过给定阈值的为尖点。

2.3 调整细分点

细分曲面是网格序列的极限，经细分得到的极限细分齿面往往与实际齿面存在偏差，尤其是特征点和特征附近的点，如图2所示，M表示初始网格，Mr表示实际齿面网格，M∞表示极限网格，V0和V1的极限位置分别为和，与实际网格点V′0和V′1存在距离误差L0和L1。上文给出了各种点的极限位置，因为Loop细分网格上的任意一点Vi在极限细分曲面上的位置可以用=Li·Vk表示，其中Li是细分矩阵对应特征值为1的左特征向量，在上文求各种点的极限位置时已求出；Vk表示极限位置只与该点的1-领域点有关。因此，可以通过对每次细分出的点搜索其1-领域点，再根据上文推导出的曲面上几种点的极限位置公式，计算其极限细分点，再与实际齿面对应的点的距离补偿相应的顶点的误差。如图3所示，粗线表示的折痕经过一次细分后，折痕顶点调整为V′2，V′0和V′1，通过折痕上细分出的奇点和偶点调整折痕附近的点（1-领域的点）V′13，V′30，V′05，V′52，V′24，V′40，V′60和V′16，再通过折痕附近的点调整折痕上的点，每次细分后都进行上述反复交叉调整。通过上文推出的不同情况下网格上任意一点在极限细分曲面上位置，可以得出通式

式中βi，j为：

从数据点集｛pi｝中找到与最近的点，设该点的极限细分曲面上与数据点集中pi的距离误差为Li，则。如果距离误差Li大于给定的阈值，则可采用文献［11］中以搜索的最近顶点位置和法向建立参数直线方程，通过让精度评价系数λ足够小、参数T正负的判断对方程进行求解，计算出空间点到极限细分曲面的最短距离，作为调整距离的误差。设由文献［11］方法计算出空间点pi到极限细分曲面的最短距离为Dplmin，空间点pi到极限细分曲面的最近点的方向量为Ni，则优化后细分网格上的点Vi的位置V′i为

对于距离误差Li大于给定阈值的控制顶点，按照式（12）优化调整后，极限细分齿面将更加逼近原始点数据，与实际齿面的偏差会更小。

2.4 细分齿面的深度估计

齿面经过k次细分后控制网格上的顶点与其在极限网格上的位置之间的最大距离定义为

由于Loop细分是一种静态细分模式，不同层次的细分矩阵都是一致的，可以得出下面的规律：Mk=CMk-1=C2Mk-2=…=CkM0。

处在第k层上的顶点V在细分网格上的位置，可以用该顶点在初始控制网格上的位置和1-领域上的顶点表示为，其中

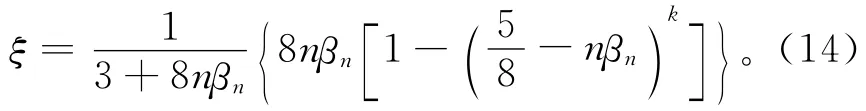
由式（11）、式（13）和式（14）可得

同理，经过k+1次细分后，

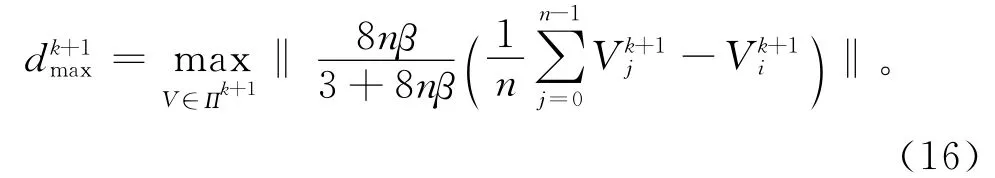
又由于细分曲面的凸包性质，同一层网格上的偶点比奇点到对应的极限曲面的距离小得多，将Loop细分模式中奇点产生的计算式（2）代入式（16）中的，经化简可得

表3所示为根据给定的精度，利用上述推导的公式对上述两种重建齿面满足精度需要的最少细分次数进行细分深度估计的结果。

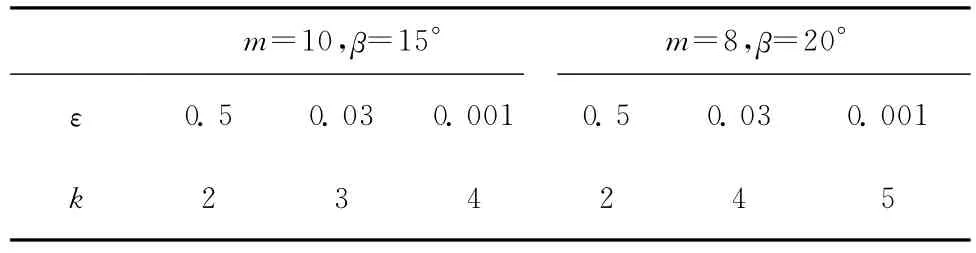
表3 满足精度需要最少的细分次数

2.5 生成细分齿面

本算法是在Intel（R）Core（TM）2 Duo CPU 2.10GHz、内存2G 的硬件平台上，应用Borland C++Builder6.0 软件实现。分别对齿轮模数m=10、齿数z=85、压力角a=20°、螺旋角β=15°、变位系数xn=0、齿顶高系数han=1、顶隙系数cn=0.25、齿宽B=160 进行重建，其重建效果如图4a所示；对齿轮的模数m=8、齿数z=45、压力角a=20°、螺旋角β=20°、变位系数xn=0、齿顶高系数han=1、顶隙系数cn=0.25、齿宽B=180进行了重建，重建效果如图4b和图4c所示。图4a是粗加工后的齿面重建效果图，从图中可以看出齿面特征带较宽，图4b是精加工后细分4次后的效果图，图4c是细分5次后的效果图，从图中明显可以看出图4c比图4b的网格更细。因此，随着细分次数的增加，重建齿面的精度也相应提高。图4d是采用文献［6］中算法重建出的齿面，通过局部特征放大图可以看出，本文算法对齿面尖锐特征的重建具有明显优势。表4所示为对本文算法与文献［6］中算法细分过程的比较，从中可以看出，无论网格规模还是系统耗时都优于文献［6］的算法。

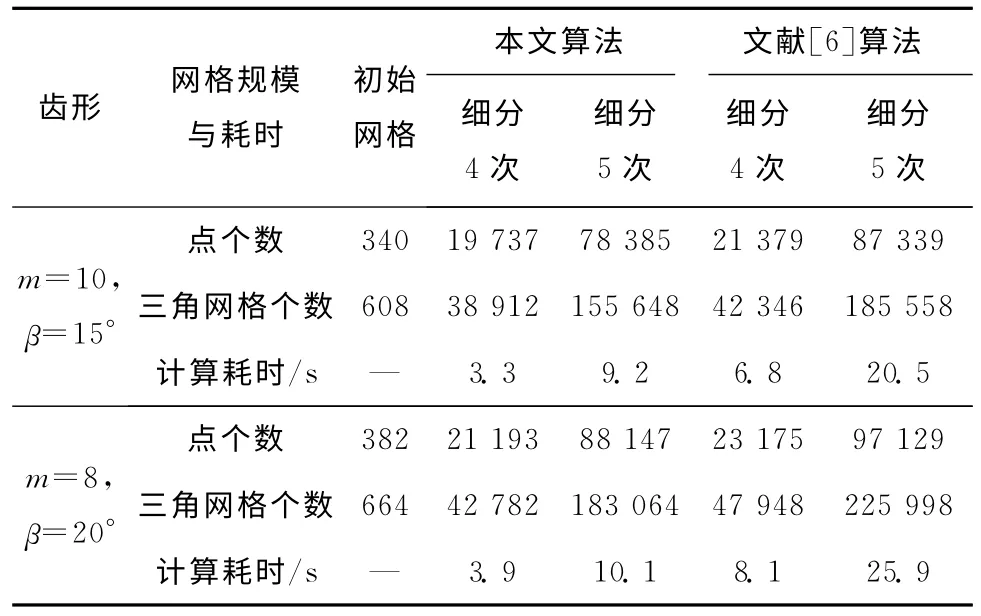
表4 本文算法和文献［6］算法细分过程的比较

3 齿面重建误差分析

为了对本文所提算法重建后的齿面精度进行验证，在江苏省工业装备数字制造及控制技术重点实验室对上述加工后模数m=8 的齿轮用WENZEL（LH1512）三坐标测量机进行采样测量，如图5所示。

为了能直观比较采用本文算法细分5次重建模数m=8的齿轮齿面与实际齿面的偏差，在MATLAB环境下对实际齿面采样点与对应的重建点进行比较，并与理论齿面对应的点也进行相应的比较，图6中的纵坐标轴（法向偏差／μm）表示与理论齿面对应点比较的结果；虚线表示真实测得的齿面数据采样点数据；实线表示重建后齿面的数据点。经比较后可知，重建后的齿面与实际齿面贴合得很好，尤其是齿面局部特征处，偏差不超过2μm，此结果说明齿面重建的效果较好。表5列举了部分测量点与重建点（细分了5次）的法向偏差数据。

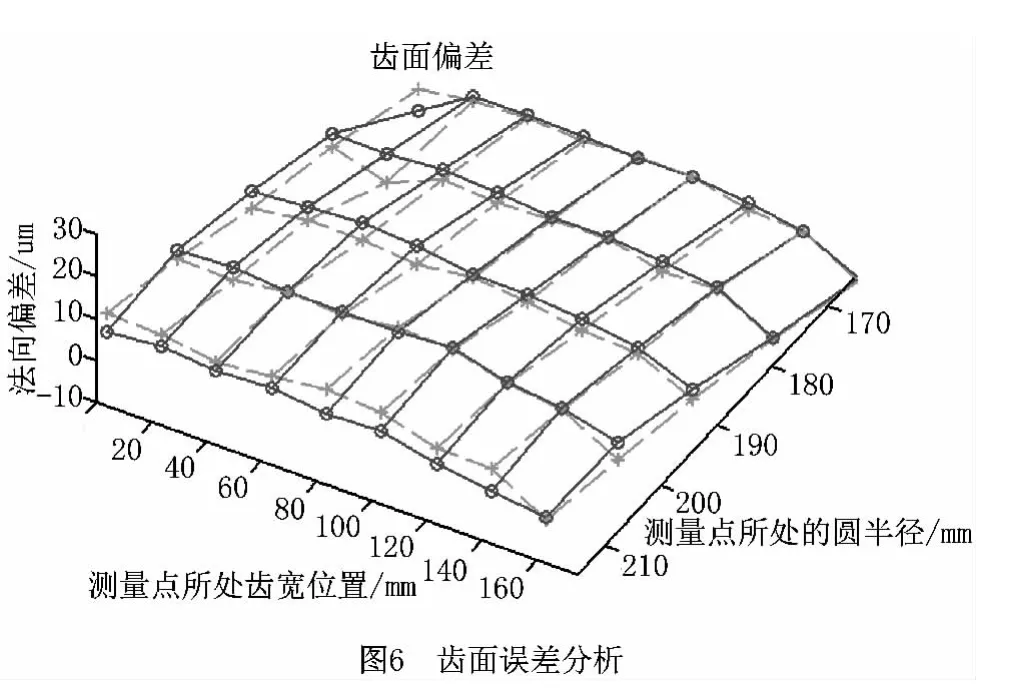
表5 测量点与重建点（细分5次）的法向偏差

4 结束语

本文在经典Loop细分方法的基础上，提出带有特征的齿面重建方法，并实现了带有特征的齿面重建。该方法首先对齿面上大量散乱的数据采用螺旋增长算法构造初始网格，然后对初始网格进行带有特征的Loop 细分，每次细分后都对细分点进行调整，详细论述了调整细分点的方法，对Loop细分进行了深度估计，最后通过重建误差分析，得出重建齿面与实际齿面偏差不超过2μm 的结论，证明了本文方法的可行性与准确性。

未来将对细分齿面与实际齿面距离算法进行深入探讨，从而进一步提高齿面拟合精度；包含齿面特征处的细分次数深度估计，也将进一步提高齿面重建的效率。

［1］PAN Hongxin.Gear modification technology research［J］.China New Technologies and Products，2011（13）：122（in Chinese）.［潘洪鑫.齿轮修形技术研究［J］.中国新技术新产品，2011（13）：122.］

［2］PAN Haipeng，CHEN Tao，HAN Wen，et al.Method of proposing 3Dof gear based on the discrete data points［J］.Mechanical Transmission，2008，23（4）：38-40（in Chinese）.［潘 海鹏，陈 涛，韩 文，等.由离散点云数据建立齿轮三维模型的方法研究［J］.机械传动，2008，23（4）：38-40.］

［3］TEWARI G，GOTSMAN C，GORTLER S J.Meshing genus-1point clouds using discrete one-forms［J］.Computer &Graphics，2006，30（6）：917-926.

［4］WANG Y，FENG H Y，DELORME F E，et al.An adaptive normal estimation method for scanned point clouds with sharp features［J］.Computer-Aided Design，2013，45（6）：1333-1348.

［5］LOOP C.Smooth subdivision surfaces based on triangles［D］.Salt Lake City，Utah，USA：University of Utah，1987.

［6］LI Guiqing，MA Weiyin，BAO Hujun.Fitting system loop subdivision surfaces with sharp features［J］.Journal of Computer-Aided Design &Computer Graphics，2005，17（6）：1179-1185（in Chinese）.［李桂清，马维银，鲍虎军.带尖锐特征的Loop细分曲面拟合系统［J］.计算机辅助设计与图形学学报，2005，17（6）：1179-1185.］

［7］BAI Jie，ZHAO Gang，YAO Fusheng.An offset algorithm for Loop subdivision surface with creases［J］.Journal of Computer-Aided Design &Computer Graphics，2008，20（10）：1261-1265（in Chinese）.［白 杰，赵 罡，姚福生.带折痕的Loop细分曲面等距面处理算法［J］.计算机辅助设计与图形学学报，2008，20（10）：1261-1265.］

［8］XING Yuan.Study on subdivision application in product with complex surface design for quality-controlling in manufacture［D］.Tianjin：Tianjin University，2010（in Chinese）.［邢元.面向加工质量细分的复杂曲面产品设计理论与技术研究［D］.天津：天津大学，2010.］

［9］ZENG Kaishan，PAN Rijing，SUN Jianpo.Algorithm and implementation of adaptive Loop subdivision surfaces for preserving sharp feature［J］.Journal of Fujian Normal University，2011，27（6）：27-32（in Chinese）.［曾锴珊，潘日晶，孙坚坡.保持特征的自适应Loop细分曲面算法及实现［J］.福建师范大学学报，2011，27（6）：27-32.］

［10］ZHOU Hai，ZHOU Laishui，WANG Zhandong，et al.Surface reconstruction from unorganized points using subdivision techniques［J］.Journal of Computer-Aided Design &Computer Graphics，2003，15（10）：1287-1292（in Chinese）.［周海，周来水，王占东，等.散乱数据点的细分曲面重建算法及实现［J］.计算机辅助设计 与图形学学 报，2003，15（10）：1287-1292.］

［11］ZHU Jianning，WANG Minjie，WEI Zhaocheng，et al.Algorithm for quickly calculating the signed distance between a point and a subdivision surface［J］.Computer Integrated Manufacturing Systems，2013，19（4）：687-694（in Chinese）.［朱建宁，王敏杰，魏兆成，等.计算空间点到细分曲面有符号最近距离的方法［J］.计算机集成制造系统，2013，19（4）：687-694.］