基于PST层次结构的改进GA求解柔性车间调度问题

栾 飞 ，王 雯，傅卫平，宝昱彤，任工昌，王 军，邓明明

（1.陕西科技大学 机电工程学院，陕西 西安 710021；2.西安理工大学 机械与精密仪器工程学院，陕西 西安 710048；3.西安财经学院 信息学院，陕西 西安 710100）

0 引言

柔性车间调度问题（Flexible Job-shop Scheduling Problem，FJSP）的核心思想是：多批次多种类零部件可以在同类别多型号设备上加工生产。在正式加工前，每个零部件的工艺是唯一确定的，但工艺路线却是不定的，每道工序有多种加工设备的选择，即每个待加工零部件有多条工艺路线可以选择，且设备选择要基于设备能力平衡。与传统的车间调度问题相比，FJSP是更加复杂的NP-hard问题，解决此类问题要求算法具有更高的复杂性，但由于它更接近生产的实际情况，使得它成为目前国内外调度领域的研究重点。

近年来，学者们对柔性车间调度也开展了大量的研究，文献［1-2］为了提高遗传算法（Genetic Algorithm，GA）的搜索速度，提出了改善编码方式优化染色体的方法，使GA 的时间与空间复杂度大大降低，但其研究的调度状况过于理论化，未能考虑环境变化，不具柔性。文献［3］结合FJSP 的特点，采用适当的策略改进了染色体编码方式、交叉算子和变异算子，大大提高了算法求解精度，但其求解速度并没有提高。文献［4］为了消除GA 只能应用于成组技术JSS的局限性，提出了JSS连锁基因编码法，虽然提高了求解效率，但其染色体的空间复杂度仍较高。文献［5-7］首先建立了JSP的赋时变迁Petri网模型，然后应用GA、模拟退火（Simulated Annealing，SA）算法、粒子群优化（Particle Swarm Optimization，PSO）算法中一种或者混合二种算法解决该问题，所用求解算法依然具有很高的时间和空间复杂度，没能同时有效地提高算法的求解速度和精度。

文献［8-9］采用更易描述数据逻辑关系的多色集合理论，排除了不可行解，极大地缩小了GA 的搜索解域，同时提出用单层编码方式表示调度问题中的双重约束，降低了算法的时间和空间复杂度，但是该文献所述算法只能在简单情况下（工序对应设备二选一）生成染色体，与实际应用差距较大；且染色体采用的分段编码是以最大工序数为基准单位生成的，从而导致算法在实践中处理大规模多工序调度问题时出现染色体太长、无效数据过多等现象，需要进一步改进。据此，本文在充分分析生产调度中的约束模型的基础上引入多层次的约束描述方法，将原来巨大的围道矩阵进行切分，降低了约束模型的冗余数据量，增加了算法实际应用的可能性；此外还改进了文献［10］的染色体编码方式，去除了大量的无效基因，从空间复杂度的角度进一步优化了算法，提高了其收敛速度。

1 柔性车间调度问题的数学模型［11］

FJSP可以被描述为：假设M为加工设备的数量，N为待加工工件数量，P为工序数，I为所有设备的集合；Ieg代表工件e第g道工序的可用设备集合，Ieg⊆I；Je为工件e的工序数。x为所有工件的加工次序，Segk表示工件e的第g道工序在设备k上加工的开始时间；Eegk为工件e的第g道工序在设备k上的加工结束时间；Tegk为工件e的第g道工序在设备k上的持续加工时间，且k∈Ieg，则有Eegk=Segk+Tegk；Ep表示最后工序的完工时间；MS表示所有工件的最后完工时间。

当工件i的第j道工序和工件e的第g道工序在同一台设备上执行时，若工序j先于工序g加工，则Qijeg=1，否则Qijeg=0；若工件e的第g道工序在机床k上加工，则Xegk=1，否则Xegk=0。

若某FJSP共有S种可能的加工顺序，要求总的作业时间最短的加工排序，应先求取每个加工顺序x（x∈｛1，…，S｝）对应的作业时间。显然，顺序x中最后加工工序的完工时间即所有工件的最后完工时间。

2 基于PST层次结构的FJSP约束模型

2.1 多色集合理论简介

多色集合理论是一个新的系统建模理论和帮助信息处理的数学工具，该理论和方法自出现后在前苏联及现在俄罗斯企业界特别是航空航天企业得到了广泛的推广与应用［12］。该理论核心思想是将相同的数学模型应用于仿真不同的对象（产品、生产系统、设计和工艺过程等），描述元素之间的层次结构和复杂关系，并在集合层与逻辑层组织并处理信息，在数量层处理低层数据实际值问题［13］。

2.2 车间实际生产约束条件分析

对于一般制造企业来说，实际的生产工作会受到大量人、机、料、法、环等因素的影响和制约，因此实际的车间调度工作需要考虑的因素众多，用普通的PST 来描述这种约束关系，会导致模型中的个人颜色、统一颜色及体的围道矩阵都具有较大的数据量。如何将多方面的影响及时地变更到描述元素关系的围道矩阵中，是应用多色集合理论和智能算法解决调度问题的一个重要瓶颈。PST 的层次结构模型为解决该瓶颈提供了有效途径。

结合大量车间调度的实际经验分析发现，如果给车间内的设备设置相应的设备基准和设备型号，则可以将工序与设备基准序进行关联，设备基准与设备代码进行关联，设备代码再与车间的具体设备的资产编号进行关联，最后间接建立工序与设备的对应关系，进而给企业的设备管理和车间调度工作带来很大便利。如果用一个单一的围道矩阵描述工序与设备的对应关系，则势必会导致矩阵过大，缺乏实用性。

2.3 基于PST层次结构的车间调度约束模型

基于上述分析，考虑车间实际生产中的各种影响因素，本文在调度过程中设置了四种约束：①工序约束是指按照实际的加工工艺，工序必须按照先后顺序进行排产；②基准约束是指一道工序只能在指定的几种基准类型的设备上加工；③机床约束是指每一个基准类型对应几种固定的机床型号；④唯一约束是指每个工件的任意一工序在固定时刻只能在一台机器上加工。其约束关系为首先设置设备基准，每个设备基准包含相似工艺的几种设备型号，每个设备型号又包含几台该种型号的具体设备，每台具体设备又与对应的资产编号对应，而工序最终要在具体设备上完成加工，因此就可以通过工序与基准的约束关系、设备基准与设备型号的约束关系、设备型号与资产编号的约束关系，间接地建立工序与具体设备的约束关系，从而实现将庞大的工序机床围道矩阵分割为小的关系矩阵，以降低矩阵的规模和数据量，提高算法的求解速度，其具体层次结构如图1所示。

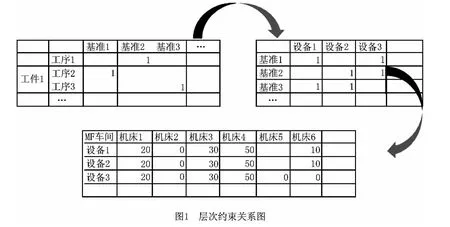
图1左上角围道矩阵反映了零件的工序约束和基准设备类型约束，即每一道工序可以由哪个基准设备类型加工，可以通过该矩阵反映出来，无值的即不可以加工；右上角围道矩阵反映了基准设备类型与具体设备型号的机床约束。其中有1的，证明该基准设备类型包含该设备型号。下方围道矩阵反映了M 车间设备型号与具体机床的对应关系，其中数值表示对应工序在该机床上的加工时间。在此基础上可以进一步得出其任务分配模型如图2所示。

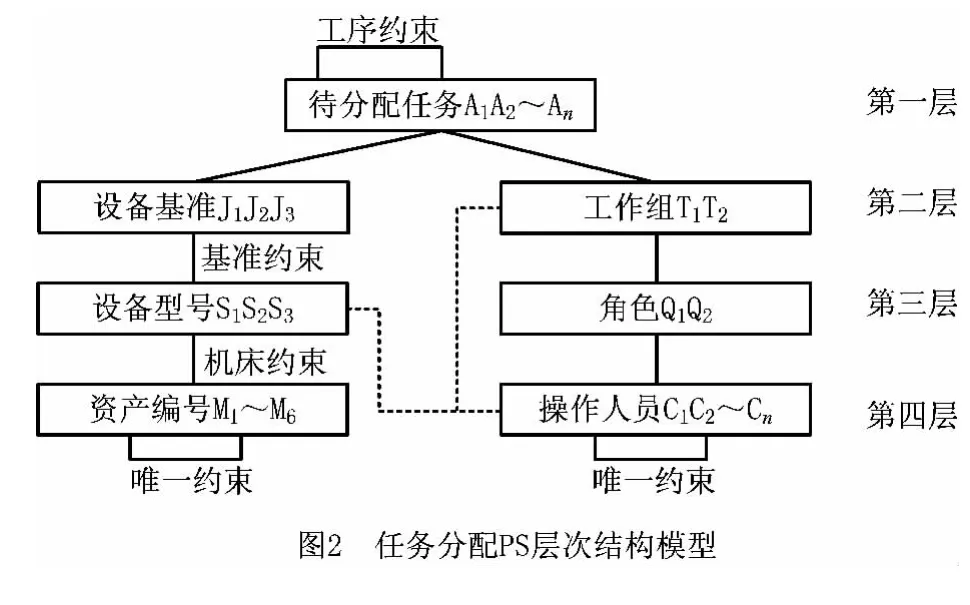
下面将通过3个工件的FJSP介绍其PST 层次结构约束模型的建立过程，其加工任务信息表如表1所示，表中列表示设备信息，行表示工件工序信息，表中的数据表示行对应工序在列对应机床上的加工时间，针对表1的相关信息和工艺相似性准则设置设备基准J1，J2和J3，设备型号为S1，S2和S3，资产编号M1，M2，M3，M4，M5和M6，即本次加工的6台设备，其相互之间的约束关系如式（5）和式（6）所示。

表1 加工任务信息表

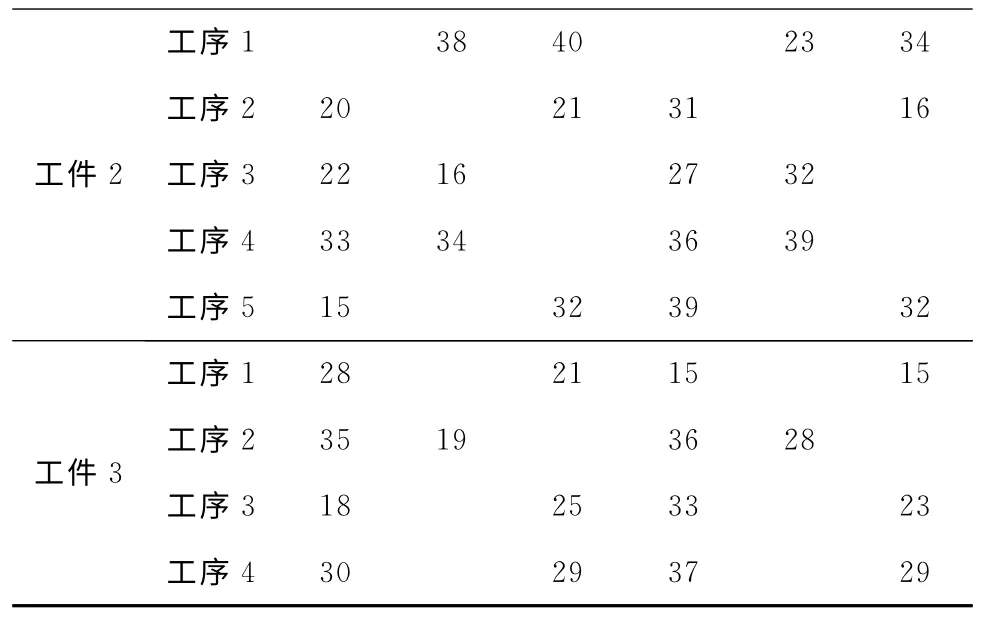
续表1

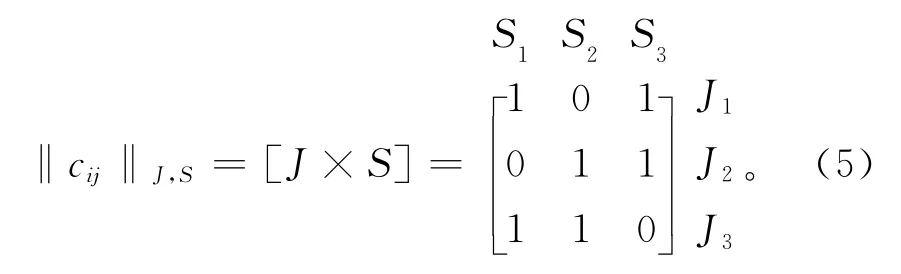
式中Cij的点位表示该点横向代表的基准所包含的设备型号。从该矩阵中可以发现基准与设备型号间的关系。

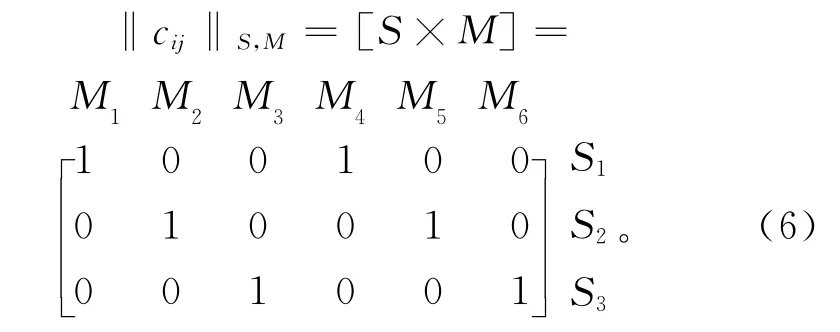
式中Cij=1的点位表示横向代表的设备型号所对应的本车间内所有设备的资产编号。

综上可以得到节点集合的自相关矩阵［F（a）×F（a）］如表2所示。

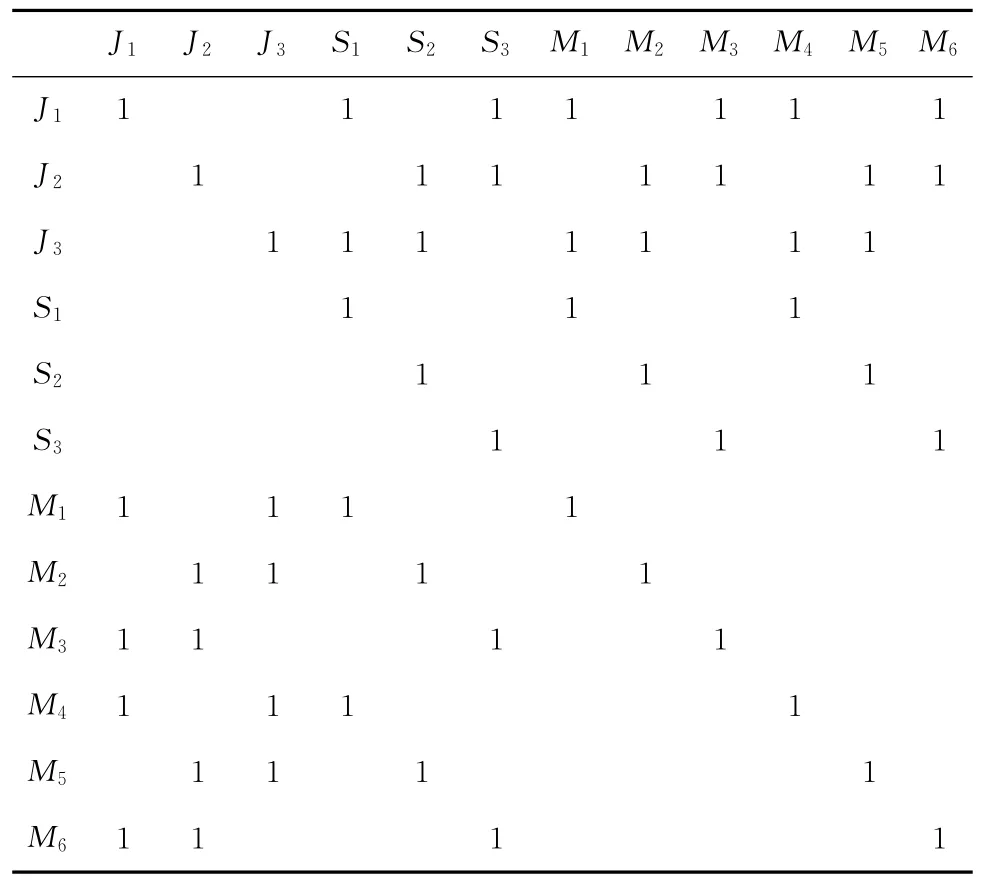
表2 矩阵［F（a）×F（a）］

根据表1相关数据和设定的工件对应的设备基准和表2中记录的各节点间的关系，可以得到围道矩阵［A×F（A）］和体的围道矩阵［A×A（F）］如表3和表4所示。其中：F1～F6代表不同的工艺名称车、钳、镗、钻孔、铣、刨；J1、J2和J3分别代表三种不同的设备基准，且在本实例中与工序一一对应；a1～a15表示3个工件的工序列；M1～M6表示待加工机床。其中，Cij=1的点表示横坐标所代表的元素与纵坐标所代表的颜色有直接联系。

表3 工艺—设备布尔围道矩阵［A×F（A）］

表4中的实数部分矩阵可以作为进一步隐性染色体编码的依据。由该矩阵可以得到可加工每一工序的设备及在该设备加工本序工作所需要的时间。

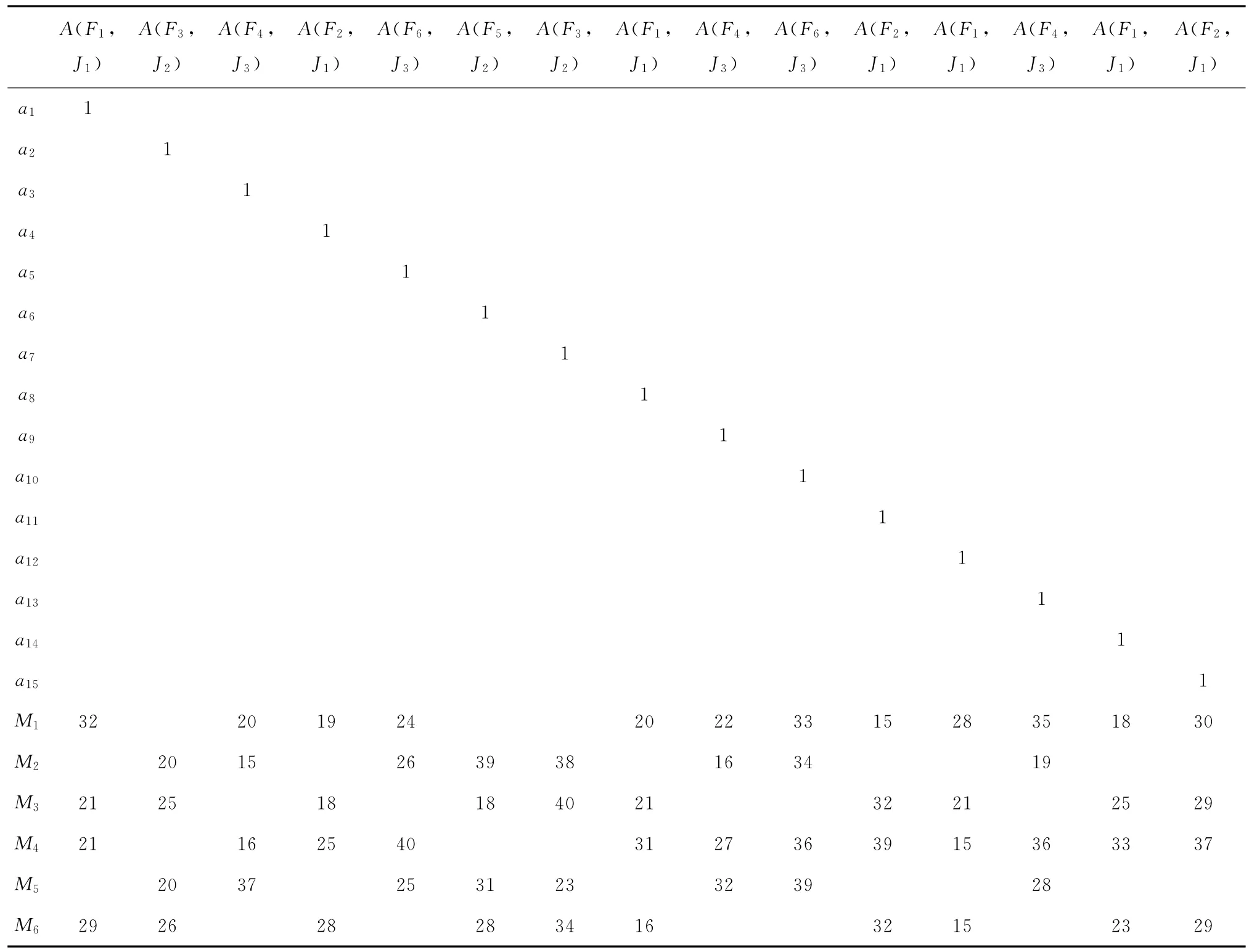
表4 工艺—设备实数围道矩阵［A×A（F）］

3 遗传算法的改进

遗传算法属于进化算法（evolutionary algorithms）的一种，通过模仿自然界的遗传与选择的过程来寻找最优解。适用于复杂问题的求解，现已被普遍应用于各个领域的研究。但是，从优化算法和使用要求的角度，学术界从来都没有停止过对该算法的改进和优化，降低算法的时间和空间复杂度。

3.1 算法的优化方向

文献［8］所提出的单层遗传编码方式在一定程度上降低了遗传编码的空间复杂度，同时在处理批量调度问题时，以产品类型作为一段染色体进行整体编码，而产品对应工序则是以隐性染色体片段的形式进行表述。在遗传求解过程中，这种编码方式在一定程度上提高了收敛速度和求解精度。

虽然文献［8］的编码方式有一定的优越性，有利于排产进行，但是染色体中存在大量的无效基因位。因为其将染色体长度定义为max（mi）×n（max（mi）为n类工件所包含的最大工序数），从而使整个染色体的长度在很大程度上决定于每个批次任务中工序数最大的一个工件。染色体过长直接影响了遗传算法在迭代过程中的效率，增加了算法的空间复杂度。

3.2 单层编码的优化

针对上述不足，本次算法的优化主要通过对染色体长度的优化和相同产品合批后编码来实现。

（1）染色体长度优化

改善前的染色体（以3零件，最大工序数为6为例）为：

改善后的染色体为：

由此，可以发现仅三个工件的染色体的长度就已经有显著缩短。从算法优化的角度，在数据量大时可以明显地降低算法的空间复杂度。文献［8-9］已经将其算法与他人研究做了对比，显示出了其优越性，将本文改进后的算法与其对比如表5所示。

表5 算法优化对比

表中：G表示遗传算法的遗传代数；Z表示交配池中初始化的染色体个数；mi为第i类工件所包含的工序数；M为设备数量；J为基准设备数（远小于实际设备数）。

（2）根据实际需求合批

多件多品种调度时：假设n类工件共有j件（j=n1+n2+…+ni+…+nn，其中n1，n2，…，ni，…，nn分别表示第i类工件的数量，且i∈n），再设每类工件有pi道工序。

文献［8］采用的方式如下：

假设有A，B，C类工件各3件，则对工件加工次序进行随机排序，生成显性染色体。

再根据工序—机床围道矩阵，生成如下隐性染色体。其中A11为A类产品的第一道工序，以此类推。

由学习曲线理论可知，重复操作可以增加员工操作的熟练度，缩短单个零件的加工时间，因此本文研究中采用同种类零件合批生产编码策略。当同种零件的数量小于100 件时，将其合并成一个任务。上述例子可以编码如下：A·3 代表其各工序加工时间都相应地乘以该系数，即该零件个数。

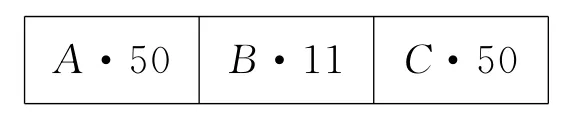
最后根据基准—设备型号，设备型号与资产编号围道矩阵，生成隐性染色体。

如果超过100则采用分批策略，因为如果一个工件的数量太多，合成一批次后会影响后续零件的加工。由于每个批次内部的零部件的交货期都不同，为满足其他零件也可以在规定的交货期到达指定库房，根据实际经验取100 件作为分批临界点。设A 工件150件，B工件211件，C工件50件，则分批后的单个任务体间是随机排序的。

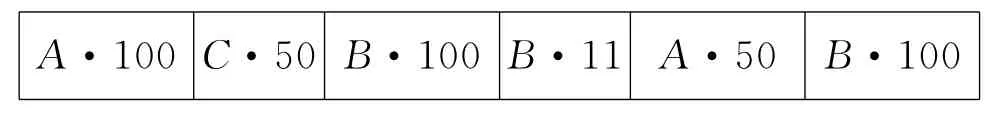
4 实例仿真

4.1 实例1仿真

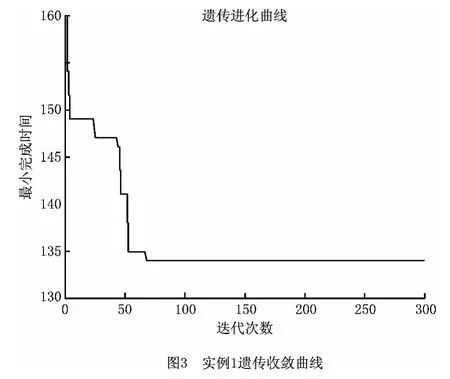
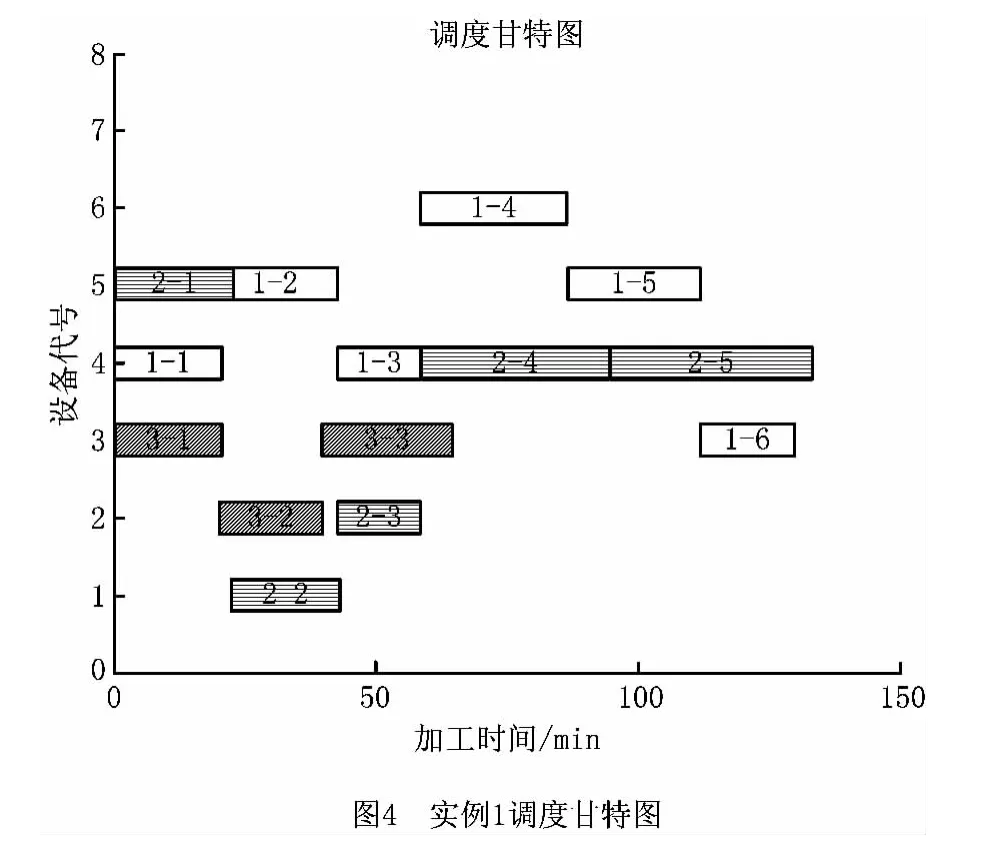
针对表1的算例，设置遗传算法的参数如下：种群大小为50，交叉率为0.6，变异率为0.8，最大进化代数100，在MATLAB 7.0环境下进行仿真，得其GA 进化曲线如图3所示，由图3可知此改进的GA 算法能够在70代时，从147较快地收敛到134，其对应调度结果甘特图如图4所示。

4.2 实例2仿真与比较

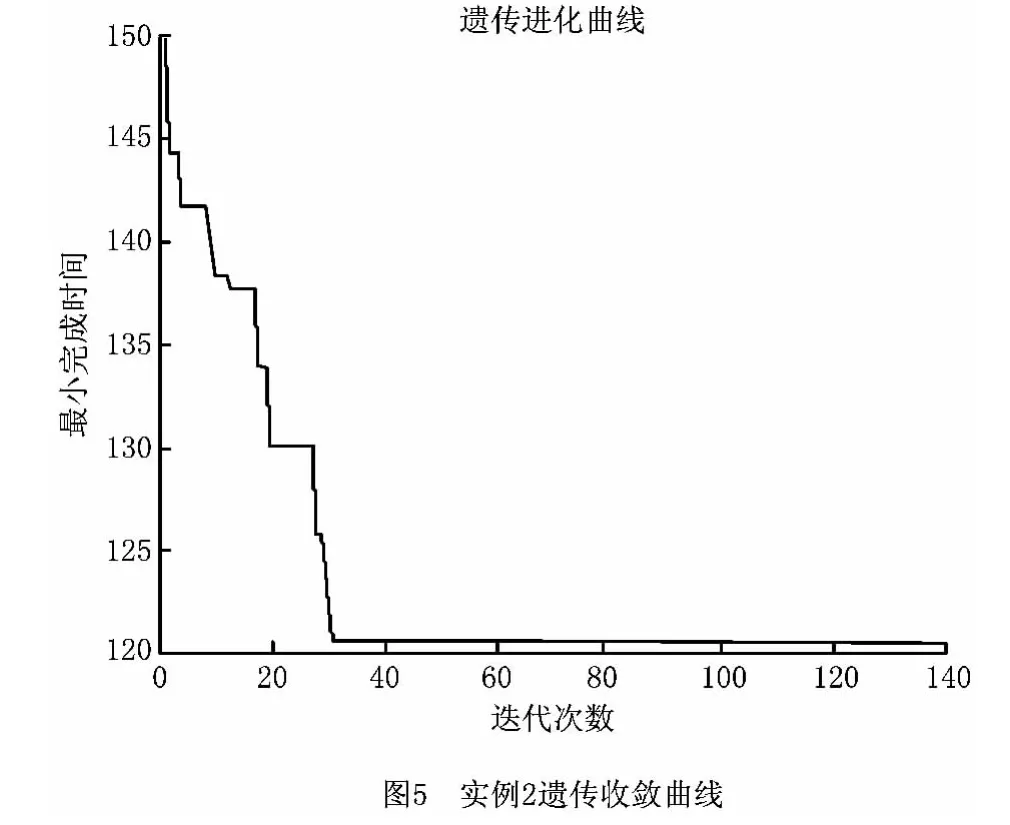
为进一步验证算法的正确性，选择文献［8］的实例2进行仿真，具体加工信息见文献［8］，设置2个工艺基准，4个设备编号，8台具体设备，遗传参数同文献［8］，得到最优解为121min。由图5的遗传进化曲线可知，当改进的遗传算法在32代时，能很快地从130收敛到121，且其求解的速度明显较快。

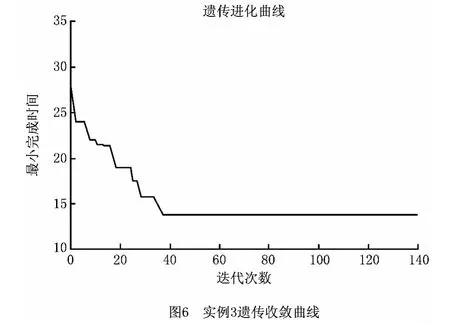
4.3 实例3仿真与比较

为更加全面地比较和验证算法效果，笔者在CPU 主频2.5G、内存512 MB 的计算机上，以VB 6.0为开发平台，选取柔性作业调度的Kacem 基准问题中的8×8实例进行求解［14］，设置2个工艺基准，4个设备编号，8台具体设备，计算10次。表6为本文算法将所得结果与文献［14］以局部最小化为分配模 型的进 化算法（Approach by Localization&Controlled Genetic Algorithm，AL+CGA）、文献［15］的主—从遗传算法、文献［16］的多阶遗传算法、文献［17］的蚁群遗传算法的求解结果对比，实例3的遗传收敛曲线如图6所示，上述算法的详细参数设置请参考相应文献。

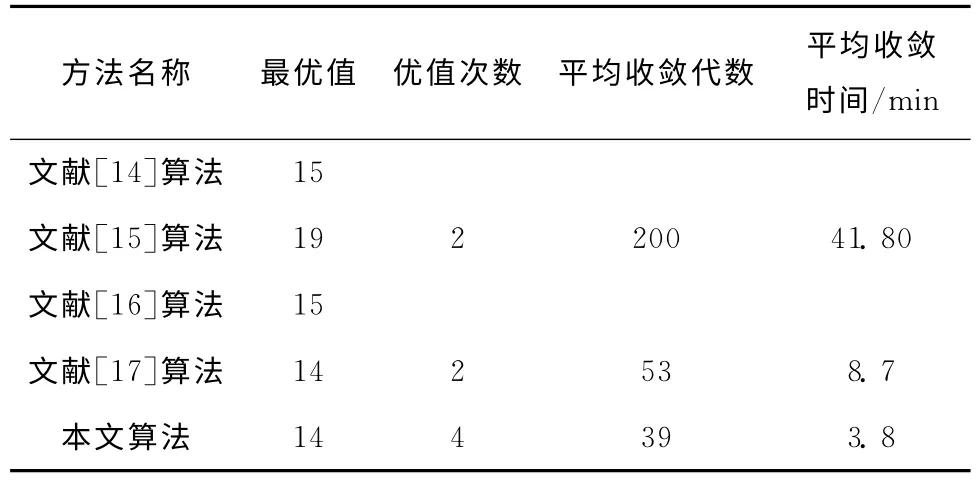
表6 Kacem 8×8基准问题各方法求解结果对比

5 结束语

本文针对传统多色集合理论改进遗传算法的约束模型和染色体中冗余数据量较大的不足，进一步提出运用多色集合层次结构模型对算法的约束模型进行改进，通过建立设备基准，设置工序约束、设备约束、机床约束、唯一约束的方式，将原来的工序—机床围道矩阵分割为基准与设备型号、设备型号与资产编号的关系矩阵，大大地降低了约束模型的冗余数据量。另外，通过对染色体长度的合理优化和设置批量基准的合批操作，有效地降低了染色体的时间和空间复杂度，同时也提高了算法模型的动态响应性。最后通过比较相同算例的仿真结果，证明了PST 层次结构的改进GA 在求解精度和速度方面都比传统的PST 改进的GA 有了提高。同时也通过选择Kacem8×8基准算例在相同配置计算机上的实验，证明了本文算法的各种性能均比传统的各种算法有了提高，从而进一步证明了算法在求解柔性作业车间调度问题方面的实用性和优越性。

［1］ZHOU Huiren，ZHENG Pi'e，AN Xiaohui，et al.New method for GA-based solution to job shop scheduling optimization［J］.Journal of System Simulation，2009，21（11）：3295-3306（in Chinese）.［周辉仁，郑丕谔，安小会，等.基于遗传算法求解Job Shop调度优化的新方法［J］.系统仿真学报，2009，21（11）：3295-3306.］

［2］PEZZELLA F.A genetic algorithm for the flexible job-shop scheduling problem［J］.Computers and Operations Research，2007，21（9）：54-61.

［3］ZHANG Guohui，GAO Liang，LI Peigen，Improved genetic algorithm for the flexible Job-Shop scheduling problem［J］.Journal of Mechanical Engineering，2009，45（7）：145-151（in Chinese）.［张国辉，高 亮，李培根，等.改进遗传算法求解柔性作业车间调 度问题［J］.机械工 程学报，2009，45（7）：145-151.］

［4］JI Shuxin，QIAN Jixin，SUN Youxian.A study of coding in genetic algorithms applied to job shop scheduling［J］.Information and Control，1997，26（5）：393-400（in Chinese）.［纪树新，钱积新，孙优贤.车间作业调度遗传算法中的编码研究［J］.信息与控制，1997，26（5）：393-400.］

［5］PAN Quanke ZHU Jianying.Optimization of shop scheduling based on Petri net &hybrid algorithm［J］.Computer Integrated Manufacturing Systems，2007，13（3）：580-584（in Chinese）.［潘全科，朱剑英.基于Petri网和混合算法的作业车间优化［J］.计算机集成制造系统，2007，13（3）：580-584.］

［6］CHEN Weimin，WANG Bo，WEI Yuke.Research on Petri net based genetic algorithm in jop-shop scheduling problem［J］.Journal of Harbin University of Science and Technology，2008，13（1）：59-62（in Chinese）.［陈维民，王 波，卫玉柯.Petri网的遗传算法在Job-Shop问题中的应用研究［J］.哈尔滨理工大学学报，2008，13（1）：59-62.］

［7］JU Quanyong，ZHU Jianying.Study on the system of dynamic job shop scheduling based on combined genetic algorithm［J］.Chnia Mechanical Engineering，2007，18（1）：40-43（in Chinese）.［鞠全勇，朱剑英.基于混合遗传算法的动态车间调度系统的研究［J］.中国机械工程，2007，18（1）：40-43.］

［8］FU Weiping，LIU Dongmei，LAI Chunwei，et al.Improved GA based on polychromatic sets theory and research on multispecies FJSP［J］.Computer Integrated Manufacturing Systems，2011，17（5）：1004-1011（in Chinese）.［傅卫平，刘冬梅，来春为，等.基于多色集合的改进遗传算法求解多品种柔性调度问题［J］.计算机集成制造系统，2011，17（5）：1004-1011.］

［9］LIU Dongmei，FU Weiping.Improved genetic algorithm for flexible job-shop scheduling proble［J］.Journal of Northwest University，2011，41（4）：611-616（in Chinese）.［刘冬梅，傅卫平.改进遗传算法求解柔性车间调度问题［J］.西北大学学报，2011，41（4）：611-616.］

［10］LAI Chunwei.Research on inproved algorithm for jop-shop scheduling under manufacturing execution system ［D］.Xi'an：Xi'an University of Technology，2008（in Chinese）.［来春为.制造执行系统下的车间调度改进算法研究［D］.西安：西安理工大学，2008.］

［11］GE Lingzhi，LI Zhekun，GAO Lei.Research on flexible mixed flow the manufacturing running system with multi-species and variable batch volume flow manufacturing part of the running system［J］.Machine Manufacturing，2011（8）：49-51（in Chinese）.［葛凌志，李浙昆，高 磊.多品种变批量零件柔性混流制造运行系统的研究［J］.机械制造，2011（8）：49-51.］

［12］LI Zongbin，GAO Xinqin，ZHAO Liping.Information modeling and optimization techniques based on polychromatic sets Theory［M］.Beijing：Science Press，2005（in Chinese）.［李宗斌，高新勤，赵丽萍.基于多色集合理论的信息建模与优化技术［M］.北京：科学出版社，2005.］

［13］PAVLOV V V.Polychromatic sets and graphs for CALS［M］.Moscow，Russia：STANKIN Press，2002：10-19.

［14］KACEM I，HAMMADI S，BOTNE P.Approach by localization and multi-objective evolutionary optimization for flexible jop-shop scheduling problems［J］.IEEE Transactions on Systems，Man and Cybernetics，Part C，2002，32（1）：1-13.

［15］ZHANG Weicun，ZHENG Pi'e，WU Xiaodan.Solving flexible job shop scheduling problems based on master-slave genetic algorithm［J］.Computer Integrated Manufacturing Systems，2006，12（1）：1241-1245（in Chinese）.［张维存，郑丕谔，吴晓丹.基于主-从遗传算法求解柔性调度问题［J］.计算机集成制造系统，2006，（12）8：1241-1245.］

［16］ZHANG Weicun，ZHENG Pi'e，WU Xiaodan.Solution to flexible jop shop scheduling problems with capacitated constraints based on ant colony&genetic algorithms［J］.Computer Integrated Manufacturing Systems，2007，13（2）：333-337（in Chinese）.［张维存，郑丕谔，吴晓丹，蚁群遗传算法求解能力约束的柔性作业车间调度问题［J］.计算机集成制造系统，2007，13（2）：333-337.］

［17］ZHANG H P，GEN M.Multistage-based genetic algorithm for flexible job-shop scheduling problem［J］.Complexity International，2005，11：223-232.