无线传感器网络中高效建立干扰模型的研究

向亦宏，朱燕民

(上海交通大学计算机科学与工程系，上海 200240)

1 概述

由于无线网络中的节点是通过广播信号来传输数据包的，位于节点附近的其他节点可以监听到这些信号，因此如果有2 个相邻节点同时进行数据传输，它们发出的信号就会互相干扰，造成数据包的丢失以及网络吞吐量的降低。现今，无线传感器网络(Wireless Sensor Network，WSN)越来越多地被部署到医疗、灾害管理等数据密集型业务中，这些业务经常因为无线通信信道繁忙而受到严重的干扰。对遭受干扰的节点的性能进行精准刻画，对拥塞控制、速率分配、信道分配等无线协议的有效运作具有重要的意义。因此，在无线传感网络中准确而快速地对当前的干扰状况进行建模变得极其重要。

本文分别提出集中式算法和分布式算法，对传感器网络中的节点建立PRR-SINR 模型，并在含有17 个TelosB 节点的WSN 中对2 种算法进行性能评估。

2 相关研究

目前，对无线网络中的干扰进行建模的方法较多，如基于跳数的模型［1］、基于距离的模型［2］和基于协议的模型［3］。这些模型都基于一个简单的假设:数据包的接收与干扰之间的关系是二元的。当符合某种条件时，数据包一定会被节点接收，反之则一定不会被节点接收。文献［4-6］中的分析表明这些模型并不精确。

在文献［5-7］中，一个被称为物理模型或者PRRSINR 的模型被提出，并被用于MAC 协议的设计中。文献［6］比较了PRR-SINR 模型和其他基于二元关系的模型，得出的结论是PRR-SINR 性能最优，利用PRR-SINR 模型可以有效提高链路调度和网络拓扑控制的性能［6-9］。

文献［9-11］通过实验表明，不同时间、不同地点，节点所测得的PRR-SINR 模型是不同的，实验结果如图1 所示。其中，图1(a)为同一个节点在不同时刻所测得的PRR-SINR 模型;图1(b)为同一个节点在不同位置所测得的模型。因此，需要为无线传感器网络中的每一个节点都建立一个PRR-SINR 模型，并周期地更新该模型。

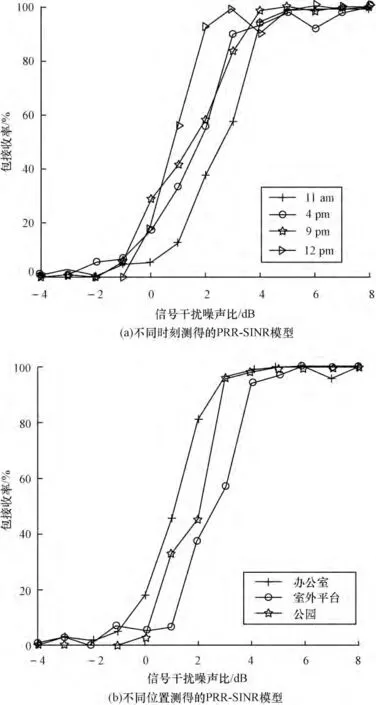
图1 不同时刻、不同位置节点测得的PRR-SINR 模型

文献［6］中采用随机选取无线传感器网络中不同的链路的方法来测量PRR-SINR 模型。文献［10］提出了一种被动式的测量PRR-SINR 模型的方法。它不需要节点主动发送测量包，而仅仅是记录各个节点发送正常数据包的时间戳以及节点成功接收数据包时的时间戳。每个节点将所记录的时间戳发送给一个中心节点，由该节点来为每个节点生成PRR-SINR模型。上述方法都需要测量很长时间才能获取整个网络的PRR-SINR 模型。为此，本文分别提出一个分布式算法和集中式算法，对WSN 中的节点建立PRR-SINR 模型。集中式算法通过一个中心节点控制节点收发测量包，使每个节点可以逐步地建立模型，分布式算法则依赖每个节点自主控制自己的收发包状况进行建模。

3 系统模型与问题描述

3.1 系统模型

在无线传输中，信号干扰噪声比(Signal to Interference and Noise Ratio，SINR)的定义如下:

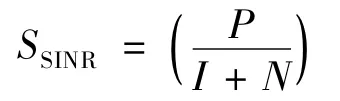
其中，P 为接收节点测量到的发送节点的发送功率;I代表的是接收节点测量到的干扰节点的发送功率;N是环境噪声。PRR-SINR 模型可以用以下公式来描述:

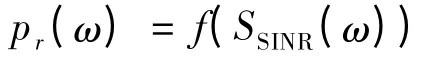
如图1 所示，PRR-SINR 模型中存在一个过渡区域。过渡区域以外的包接收率为0 或者100%。而过渡区内的包接收率在0～100%之间。因此，只需要考虑如何刻画过渡区域即可。因为大多数传感器节点的RSSI(接收信号强度寄存器)能够提供的RSS(接收信号强度)值的精度为1 dBm，所以信号与干扰的RSS 值的差值精度为1 dB，此差值即为所求SINR。文献［6］经过实际测量，得出过渡区间在［0，5 dB］，因此，仅需要为每个节点测量6 个整数SINR 所对应的PRR 即可为该节点构建完整的PRR-SINR模型。

3.2 问题描述

本文的目标是使用最少的测量包来为WSN 中的每一个节点构建PRR-SINR 模型。基本方法如下:在WSN 中选取一些节点作为一个发送子集。这个子集中的每个节点从某个时刻开始需要同时以相同的间隔发送指定数目(M)的测量包。从发包开始到结束的这段时间称为一个轮次。可以认为每个节点事先都已经测量了该节点接收其邻居节点发出的数据包的RSS，并且这些RSS 在短期内不会变化。

例:图2 中r1，r2，r3 组成了一个发送子集，其中，r2 是m 的邻居节点，r1 和r3 是干扰节点，图中虚线代表干扰链路。

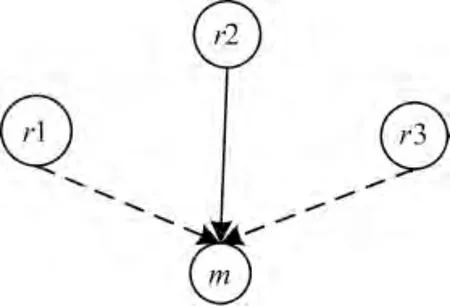
图2 PRR-SINR 点的测量

轮次开始后，这3 个节点同时发包。m 节点在此轮中处于监听模式。它收到r2 发出的包时，从RSSI 中读取接收此包的RSS(包含了背景噪声，r1，r3 的干扰信号强度)。由于r2 是m 的邻居节点，因此m 节点保存了在无干扰的情况下，接收r2 数据包的RSS。m 节点可以据此计算出接收此包的SINR:

如果得出的SINR 还没有对应的PRR 值，那么m 在此轮中只统计接收到的r2 发出的数据包的个数。在该SINR 下，节点m 的包接收率公式为:

则称在该发送子集下，m 获取了一个PRR-SINR点。

通过上述步骤，可以逐步为网络中的每一个节点构造PRR-SINR 模型。本文选择K 个发送子集组成一个发送集合S。当一个发送子集形成的轮次结束后，节点m 可以获取0 个或1 个PRR-SINR 点。令fs(nodem)≥N 代表发送集合S 中的发送子集都发完测量包后，节点m 总共可以计算出的PRR-SINR点的个数。每个节点需要在过渡区域中获取至少N 个PRR-SINR 点，即需要满足以下条件:

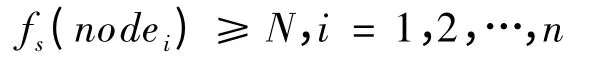
因为一个发送子集中的每个节点都需要发送M 个测量包，所以为了达到使用最少测量包的目标，笔者希望选择K 个发送子集，这些子集含有的节点的数目的和是最少的。本文问题描述如下:

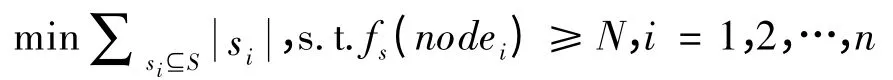
3.3 复杂度分析

引理1 选择集问题是NP 的。

证明:NP 类由这样的问题∏组成，对于这些问题存在一个确定性算法A，该算法在对∏的一个实例展示一个断言解时，它能在多项式时间内验证解的正确性［12］。

在本文的选择集问题中，如果给定一个发送集合S={s1，s2，…，sk}，则需要验证是否有:

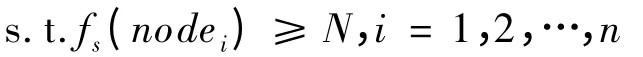
引理2 集合覆盖问题可以归约到选择集问题。

证明:给定集合W={w1，w2，…，wm}和V={v1，v2，…，vt}，vi为W 的子集。集合覆盖问题可以描述为:

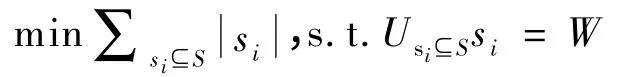
其中，S 为V 的一个子集，si为S 中的元素，为si的权重。集合覆盖问题即要求从V 中找到一个子集，这些子集中元素的并集包含了W 中的每个元素，并且子集中元素的权重的和最小。

在本文的选择集问题中，如果一个发送子集si可以使节点i 获取一个PRR-SINR 点，则称si覆盖了节点i。si的权重为si中发送节点的个数。令N=1，如果S*={s1，s2，…，sk}是本文选择集问题的解，也就是说找到了一个集合S*，它满足每个节点都被覆盖一次的条件。显然，这个解也就是集合覆盖的解。也即当且仅当S*为选择集问题的解时，S*为集合覆盖的解。因此，可以把集合覆盖问题归约到选择集问题。

定理 选择集问题是一个NP 完全问题。

证明:由引理1 和引理2 可以得出，选择集问题是一个NP 完全问题。

4 集中式算法

在集中式算法中，要求网络中每个节点都需要事先测量收到邻居节点数据包时的RSS，然后将这些数据发送给一个中心节点。中心节点使用这些数据模拟出一个发送子集，测试那些不在发送子集中的节点能否通过此发送子集获取一个PRR-SINR点，进而计算出建立整个网络的PRR-SINR 模型所需要的发送子集的集合。中心节点完成计算后，在每一个轮次开始之前告诉其他节点在该轮如何表现，例如直接加入发送子集充当发送者，或者只是统计收到某个节点发出的数据包的个数，从而构建某个PRR-SINR 点。

由于选择集问题是一个NP 完全问题，因此本文提出一个贪心随机算法，该算法部署在中心节点上，能在多项式时间内提供一个近似解。算法的具体步骤如下:

(1)发送子集集合S={}。

(2)发送子集si清空。

(3)随机从网络中选择一个节点加入到发送子集si，将Xmax设置为0。

(4)遍历所有不在发送子集中的节点，测试将该节点i 临时加入到发送子集后，能获取PRR-SINR 点的节点的个数X。

(5)选择步骤(4)中最大的X 以及对应的节点i，如果X 大于Xmax，那么将节点i 正式加入发送子集si，将Xmax设置为X，继续4)。如果Xmax为0 的次数超过了一个阈值，则跳转到步骤(7)。

(6)如果Xmax大于0，将该发送子集si加入S，判断每个节点是否都已经建立了PRR-SINR 模型，如果仍没有建立，则继续执行步骤(2)。

(7)结束。

5 分布式算法

在集中式算法中，由一个中心节点来决定网络中的节点是否加入发送子集中。而在本文提出的分布式算中，每个节点需要自己来判断是否成为发送子集中的一员。只有当发送子集形成后，其他节点才能获知自己能否通过此子集来得到一个未使用过的SINR 点。因此，节点不能预知自己做出的决策是如何影响其他节点的。本文通过一个启发式的方法来帮助节点判断自己是否加入发送子集。

如3.1 节所述，需要为每个节点测量6 个SINR所对应的PRR。本文根据这个事实来给每个节点提供决策依据:当节点得知它的邻居还需要计算的PRR-SINR 点数的平均值大于本节点剩余PRR-SINR点数时，节点以概率P1(大于0.5)加入发送子集，否则节点以概率P2(小于0.5)加入。这样，可以让那些还需测量更多PRR-SINR 点数的节点优先充当接收者，从而尽可能地测量出更多的PRR-SINR 点。为了让节点更有效地参与建模，定义另一个规则:如果某个节点在一轮结束后发现它的邻居节点的PRR-SINR 点数与上一轮是一样的，那么认为该节点在此轮中的表现是无价值的，需要对该节点进行惩罚，即如果该节点在此轮中是发送者，那么在下一轮中，需要降低该节点充当发送者的概率;同样的，如果该节点在此轮中是接收者，那么在下一轮中该节点将更有可能充当发送者。

实验结果表明，上述规则可使发送节点的数目减少约33%。本文将发送轮次限制为N，力图保证模型精度的前提下，使用尽可能少的节点发送测量包。

分布式算法部署在网络中的每个节点上，算法的具体步骤如下:

(1)节点以概率P 确定自己是否加入发送子集充当发送者，充当发送者的话，节点开始以固定频率发送测试包。发送完指定数目的测试包后，转入步骤(3)。

(2)节点i 充当接收者，处于监听模式。当成功收到节点K 发送的测试包时，计算此时的SINR，如果该SINR 没有对应的PRR，则接下来节点i 只统计收到K 发送的包的个数，计算PRR。

(3)各个节点对外广播自己还剩余的PRR-SINR点数。其余节点更新邻居还剩PRR-SINR 点数。据此计算出节点在下一个轮次充当发送者的概率。

(4)如果已进行的轮次数目没有达到N，则继续步骤(1)。

(5)结束。

6 性能评估

本文实验平台由17 个运行TinyOS-2.02 系统的TelosB 节点构成，一个节点充当中心节点，其余16 个节点均匀分布在4 m ×4 m 的空间上。上文所述的集中式算法和分布式算法均在此平台上进行性能评估。

6.1 精度评估

本文采用文献［5-7］中使用的一种主动干扰测量方法(简称ACTIVE 方法)来与本文提出的方法进行比较。该方法通过m 轮的测量，为一个节点构造生成一个PRR-SINR 模型。当要为节点m 生成模型时，先为m 节点选取一些辅助节点，这些辅助节点负责在每一轮中以相同的时间间隔广播数据包。m 节点事先知道接收这些节点发出的数据包的RSS。这样，m 节点在每一轮选取一个辅助节点r，计算此时的SINR 以及接收到的r 发出的包的个数。通过改变辅助节点的发送功率，m 节点可以计算出不同的SINR，从而生成一个完整的PRRSINR 模型。文献［5-7］的实验结果表明，如果轮次足够多，则上述方法建立的PRR-SINR 模型可达到较高的准确率。

本文以4 096 轮次的ACTIVE 方法所构建的PRR-SINR 模型为基准，评估本文提出的方法的精确性。实验的具体步骤如下:

(1)使用集中式算法测得整个网络的PRR-SINR模型。

(2)使用分布式算法再次为每个节点构造PRR-SINR模型，重复多次。

(3)通过ACTIVE 方法为每个节点生成PRRSINR 模型。

(4)将集中式算法和分布式算法为每个节点所计算的模型与ACTIVE 生成的相比较，计算出节点过渡区域中每个SINR 对应的PRR 与ACTIVE 相比的绝对误差值。

2 种算法为每个节点生成模型的平均误差累计分布函数(Cumulative Distribution Function，CDF)图如图3 所示。其中，分布式算法轮次分别限制为30 轮和100 轮。可以看出，集中式算法得到的PRR-SINR模型精度较高，最大平均误差为5.7%，中值只有4.6%。30 轮的分布式算法所得模型最大平均误差9.4%，中值为7.0%。100 轮的分布式算法精度有一定提升，最大平均误差6.5%，中值降到4.5%。

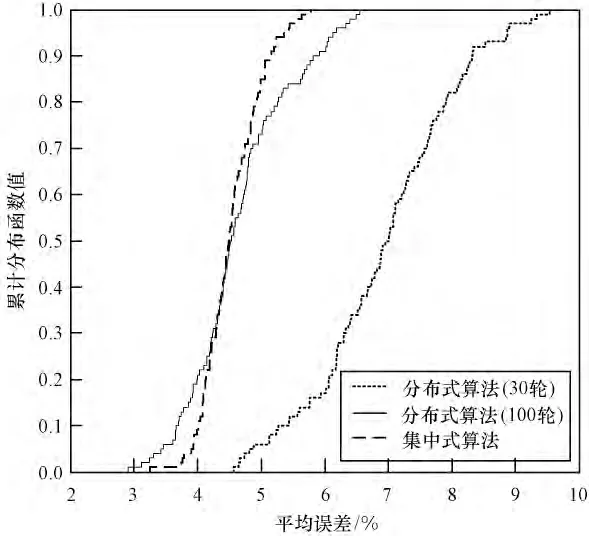
图3 2 种算法所得模型的平均误差CDF 图

6.2 开销评估

本文用实验中收集的数据在PC 上穷举所有可能的发送子集集合，从满足条件的集合中，找出最少的发送者数目，然后将之与集中式算法和30 轮分布式算法进行比较，结果如图4 所示。可以看出，集中式算法平均所需的发送者个数与最优解很接近，其最差的表现也不超过最优解的2 倍。分布式算法平均只需要2 倍于最优解的发送者，最差时也只需要4 倍的发送节点。

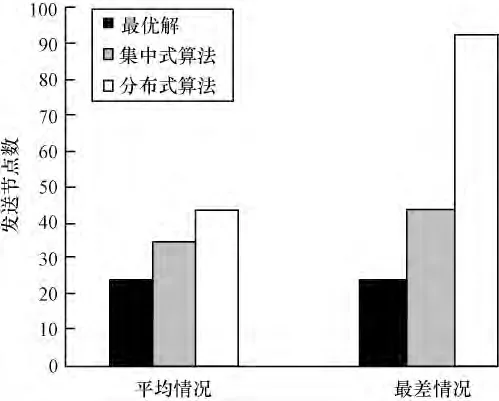
图4 2 种算法所需发送节点数与最优解的比较

在集中式算法和分布式算法中，发送节点每10 ms发送一个测量包，每轮一共发送100 个，每轮耗时1 s。实验中，集中式算法平均需要14 轮，最多16 轮来完成网络模型的建立，即集中式算法需要平均耗时14 s，最差时耗时16 s 来建立模型。分布式算法指定使用30 轮来进行测量，因此耗时30 s 构建网络模型。从对文献［10］方法的实验结果看，为达到中值平均误差7%，其需要耗时2.5 min。因此，可以看出，本文提出的2 种算法在时间开销上性能较好。

7 结束语

随着无线传感器网络越来越多的被部署到医疗、灾害管理等各项数据密集型业务之中，网络中节点信息传输的干扰也越来越受到重视，如何高效地为节点建立干扰模型成为研究热点。本文提出了2 种高效建立PRR-SINR 干扰模型的方法，一种是集中式的，另一种是分布式的，分别用于不同的场景。从实验的结果可以看出，2 种算法都具有较高的精度，而且建立模型所需时间较短，额外的开销较少。下一步工作将对分布式算法进行优化，在提高其精度的同时，进一步减少所需发送节点的数目。

［1］Sharma G，Mazumdar R，Shroff N.On the Complexity of Scheduling in Wireless Networks［C］//Proceedings of MobiCom'06.Los Angeles，USA:ACM Press，2006:227-238.

［2］Alicherry M，Bhatia R，Li L E.Joint Channel Assignment and Routing for Throughput Optimization in Multi-radio Wireless Mesh Networks［C］//Proceedings of MobiCom'05.Cologne，Germany:ACM Press，2005:58-72.

［3］Gupta P，Kumar P R.The Capacity of Wireless Networks［J］.IEEE Transactions on Information Theory，2000，46(2):388-404.

［4］Zhao J，Govindan R.Understanding Packet Delivery Performance in Dense Wireless Sensor Networks［C］//Proceedings of SenSys'03.Los Angeles，USA:ACM Press，2003:1-13.

［5］Son D，Krishnamachari B，Heidemann J.Experimental Study of Concurrent Transmission in Wireless Sensor Networks［C］//Proceedings of SenSys'06.Boulder，USA:ACM Press，2006:237-250.

［6］Maheshwari R，Jain S，Das S R.A Measurement Study of Interference Modeling and Scheduling in Low-power Wireless Networks［C］//Proceedings of SenSys'08.Raleigh，USA:ACM Press，2008:141-154.

［7］Sha Mo，Xing Guoliang，Zhou Gang，et al.C-mac:Model-driven Concurrent Medium Access Control for Wireless Sensor Networks ［C］//Proceedings of INFOCOM'09.Rio de Janeiro，Brazil:IEEE Press，2009:1845-1853.

［8］Brar G.Blough D M，Santi P.Computationally Efficient Scheduling with the Physical Interference Model for Throughput Improvement in Wireless Mesh Networks［C］//Proceedings of MobiCom'06.Los Angeles，USA:ACM Press，2006:2-13.

［9］Rangwala S，Gummadi R，Govindan R，et al.Interference Aware Fair Rate Control in Wireless Sensor Networks［C］//Proceedings of SIGCOMM'06.Pisa，Italy:ACM Press，2006:62-74.

［10］Liu Shucheng，Xing Guoliang，Zhang Hongwei，et al.Passive Interference Measurement in Wireless Sensor Networks［C］//Proceedings of ICNP'10.Kyoto，Japan:IEEE Press，2010:52-61.

［11］Huang J，Liu S，Xing G，et al.Accuracy-aware Interference Modeling and Measurement in Wireless Sensor Networks［C］//Proceedings of ICDCS'11.Minneapolis，USA:IEEE Press，2011:172-181.

［12］Alsuwaiyel M H.算法设计技巧与分析［M］.吴伟昶，方世昌，译.北京:电子工业出版社，2010.