一种基于调节因子的小生境粒子群优化算法

王 甫，郑亚平，刘天琪

(1.绵阳师范学院数学与计算机科学学院，四川 绵阳 621000;2.四川大学电气信息学院，成都 610065)

1 概述

通过模拟鸟群社会行为，根据群智能的演化计算技术，粒子群优化(Particle Swarm Optimization，PSO)算法于1995 年被提出［1］。算法中参数少、程序编制容易、具有较快的收敛速度是PSO 的明显优势，在工程中的各领域得到了广泛应用。

基于差分方程，PSO 算法的稳定性和收敛性已经得到初步结论，即基本的PSO 算法不能收敛到全局最优值［2］。对于目前流行的PSO 算法，参数选择或动态修改某个参数是改进的基本方向，但是依靠调节惯性权重和加速因子，目前仍然不能有效解决PSO 易陷入局部最优的问题。种群后期进化中的趋同性，是陷入局部最优的根本原因。如果利用多种群协同进化，加强全局收敛，就可以避免早熟。

混沌变异的小生境粒子群优化算法(Niche Chaotic Mutation PSO，NCPSO)于2002 年被提出，其中圆形小生境粒子种群在进化过程中得以实现，低维函数测试搜索精度较高［3］，协同策略实现较为复杂，但是利用小生境容易实现，可以使得小范围的粒子相互独立，形成孤立的动态搜索空间。粒子小范围有效地分布，各个粒子在自己搜索范围内寻找极值点，可以有效防止大规模的种群趋同现象。通过建立淘汰更新机制，淘汰最劣粒子，保证整个种群向全局最优值运动。

此后，NCPSO 得到了广泛的应用。2010 年，一种基于NCPSO 的图像分割方法被提出。该方法利用NCPSO，通过建立小生境，保持了粒子的多样性，一定程度上使得PSO 容易陷入局部问题得到解决［4］。通过最大类别间的方差阈值分割技术，NCPSO 得到分割图像的最佳阈值。这种基于混沌粒子群算法(Chaos PSO，CPSO)的新方法与基于PSO 的最大类别间的方差分割法进行相比，结果证明新方法可以对图像进行快速精确地分割。文献［5］提出了一种新的小生境粒子群算法(MNCPSO)。基于Mamdani 利润模型，产品价格与顾客需求量满足经济学中线性需求关系。为了求解优化模型的参数，MNCPSO 用混沌算法变换进行初始化，基于欧氏距离公式和阈值保持粒子的多样性，进一步扩大了粒子搜索范围。

尽管目前NCPSO 和相应的改进算法已经取得了不错的效果，但是NCPSO 和部分改进PSO 对高维函数搜索精度偏低、种群收敛速度后期较慢。本文针对上述缺点，提出一种改进的NCPSO 算法(NCPSO-FLV)。在算法中增加速度和位置调节因子，从而在后期的进化中，针对早熟的粒子加大随机性，提高后期的收敛速度和算法的搜索精度。

2 带有调节因子的小生境粒子群优化算法

2.1 基本粒子群优化算法

基本PSO 算法利用如下公式来通过速度和位置更新粒子状态:

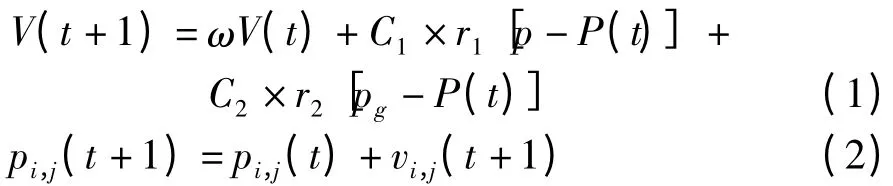
其中，pi，j表示局部最优值;pg表示全局最优值;C1和C2代表学习因子;ω 代表惯性权重。

2.2 小生境粒子群优化算法

NCPSO 基本思想是不同粒子之间不进行信息交互独立进化，使得粒子处于分离孤立的小环境中，算法中孤立环境内粒子减小了趋同性［6］。如果某一个微粒适应函数值在连续迭代的过程基本不变，以这个粒子为中心，和离它最近微粒的距离作为半径，形成圆形区域的小生境，如果粒子进入圆形区域会被吸收，并且合并成新的小生境。

算法中的小生境可以用如下公式描述:

如果粒子满足如下公式，将采取不同的操作:

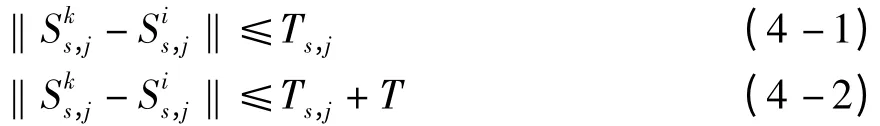
满足式(4 -1)，小生境粒子吸收粒子;满足式(4 -2)，合并小生境相交。粒子的速度更新公式如下:

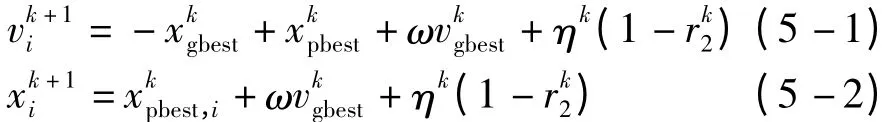
2.3 调节因子

调节因子主要在进化后期过程中被使用，其主要功能是:(1)阻止小生境中的部分粒子陷入早熟;(2)调节后期进化的收敛速度。调节因子分为位置调节和速度调节因子2 类。如果检测到种群在给定循环次数内没有位置改变时，位置调节因子认为粒子陷入局部最优，当前粒子全局搜索能力最差，算法利用全局最优值位置，更改种群中其他粒子的位置，增强了搜索能力，公式即为:

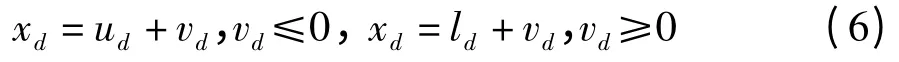
其中，xd和vd分别为粒子第d 维的位置和速度;ud和ld分别为粒子第d 维空间的最大最小值。

被调节粒子位置后，如果在规定的循环次数内最优位置仍没得到更新，再次以当前最佳位置作为参考，增强粒子的多样性。

为保证收敛性，粒子速度变化的情况必须被同时评估，又引入了速度更新因子，如果粒子速度在迭代过程中越来越慢，则种群趋向成熟，根据当前粒子中最快速度，可以使其他粒子加快运动。

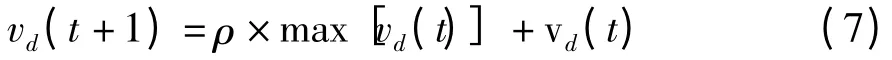
引入速度因子的目的是:当粒子当前位置与最优位置之间存在较大差距，更新后期粒子运动速度会变慢，趋向成熟收敛［7］。同时过慢的速度导致粒子难以收敛。速度因子可以作为位置因子的补充，保证一定的收敛速度，使粒子速度更新之后保证收敛。

NCPSO-FLV 算法的具体步骤如下:

Step 1给定初始化空间，产生随机粒子和速度。

Step 2根据目标函数和所有产生粒子，计算目标函数取值。

Step 3计算全局最优值。

Step 4根据式(5 -1)和式(5 -2)更新种群中所有粒子的位置和速度。

Step 5评估粒子的当前位置和上次迭代位置的变化，根据阈值，利用式(6)更新所有粒子的位置。

Step 6评估粒子的当前速度和上次迭代速度的变化，根据阈值，利用式(7)更新当前粒子的速度。

Step 7评估目标函数与全局最优值。

Step 8如果目标函数值较大，不改变全局最优值;如果全局最优值较大，用目标函数值替换全局最优值。

Step 9判断是否满足最大进化代数，不满足转Step4;满足转Step10。

Step 10结束。

3 算法对比实验

3.1 测试函数和环境

根据文献［6］选择测试函数。表1 中是从Benckmark 测试集中所选择的不同测试函数［8-9］，可以综合评价算法的性能。通过评估，可以评价算法精度和对陷入局部最优问题的处理能力。

表1 测试函数

算法测试环境为:硬件系统:CPU 为Core I 7 3630QM的CPU，内存为8 GB DDR 3;软件系统:操作系统为Win7 32 bit，使用Matlab R2010。

5 个不同函数的搜索区间均为［-100，100］。搜索区间也是PSO 粒子初始化的区间，首次循环开始，粒子在上述对应的区间内随机产生［10］。

利用小生境保持多样性，保证粒子不会陷入早熟，比较小生境粒子群和评估收敛速度和搜索精度。

3.2 测试结果

对上述3 种算法重复运行30 次，设定最大循环为10 000 次，对每个算法运行结果求出平均值，得到最后的精度比较。由表2 可见，NCPSO-FLV 的最终搜素精度较高，尤其是在第5 个带有三角函数的测试函数上，均比其他2 种算法的搜索精度高。

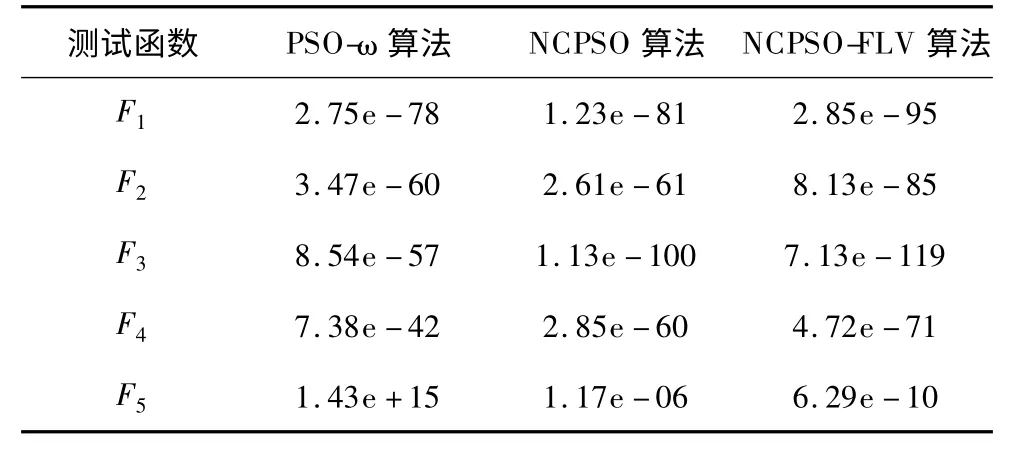
表2 3 种算法的搜索精度对比

根据设定的可接受精度，进行50 次实验，选取各个算法能够达到可接受精度的最小进化代数进行对比，结果如表3 所示。可以看出，NCPSO-FLV 所需要的进化代数最小，PSO-ω 在第5 个测试函数上在10 000 次进化后，达不到接受精度。

根据可接受精度和达到可接受精度的平均循环次数，连续运行3 种算法50 次，利用其中达到可接受精度的次数与总循环次数之比为成功概率，从表4可以看出，NCPSO-FLV 的成功概率较高，第一个函数为100%，最后一个函数和NCPSO 成功概率相同。

重复实验50 次，得到3 种算法的达到可接受精度的平均时间，结果如表5 所示。因为NCPSO-FLV引入速度限制和位置限制，进化过程比较复杂，在前4 个函数的运行时间比其他2 种算法长，在第5 个函数上的运行时间最短，也说明了NCPSO-FLV 具有对三角函数的良好搜索能力。

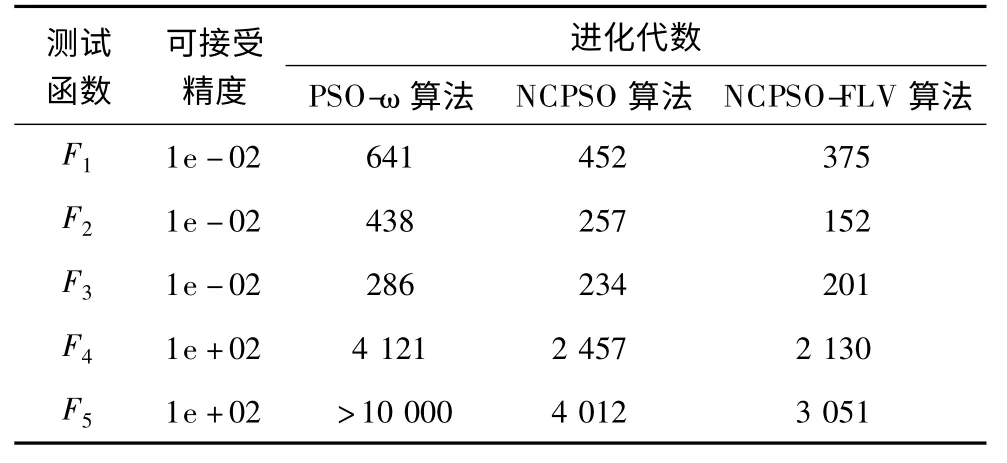
表3 3 种算法达到可接受精度的进化代数对比

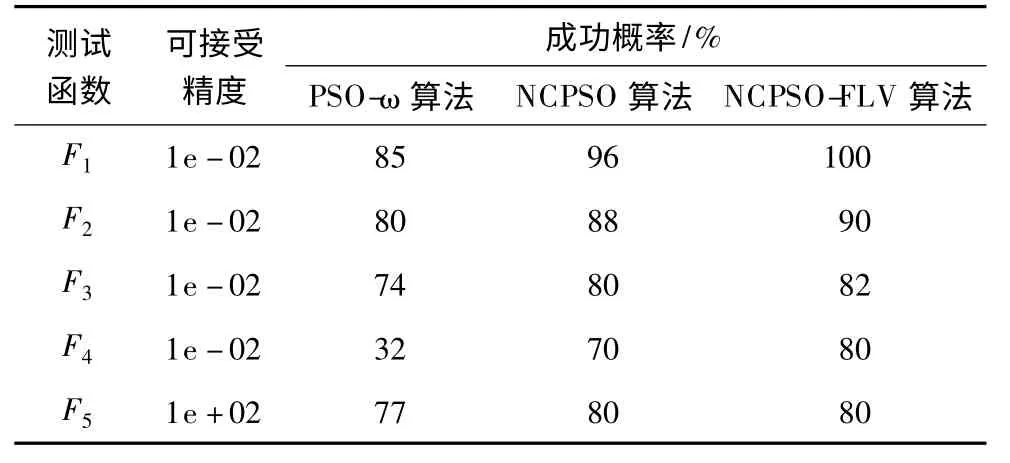
表4 3 种算法的成功概率对比

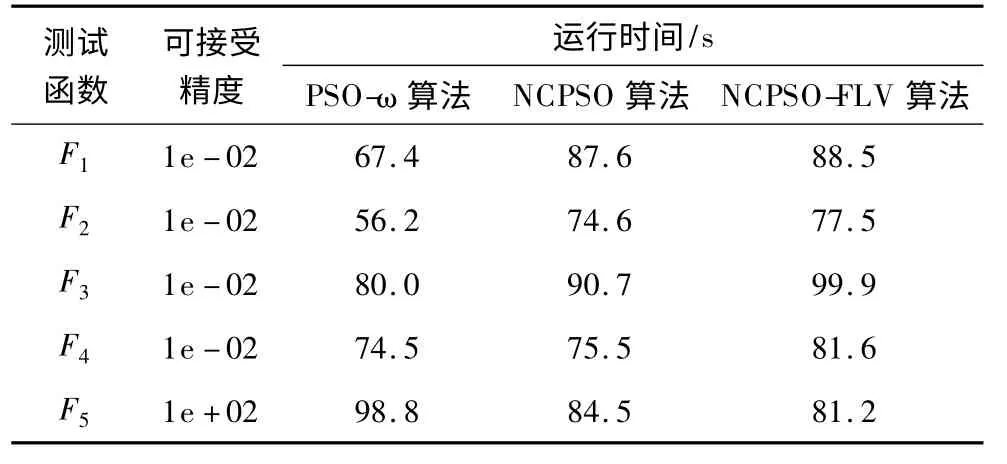
表5 3 种算法的运行时间对比

3 种算法针对5 个测试函数的收敛曲线比较如图1～图5 所示。

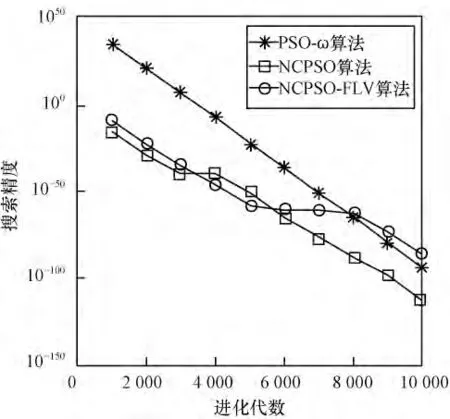
图1 测试函数F1的收敛曲线

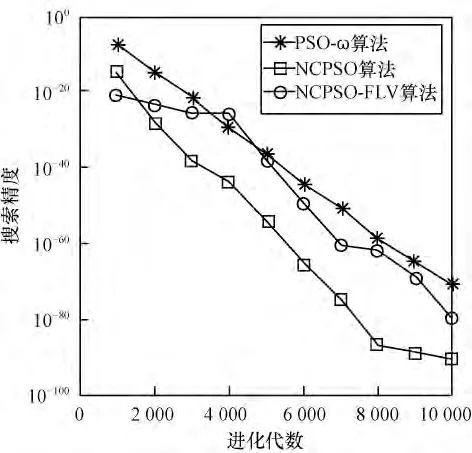
图2 测试函数F2的收敛曲线

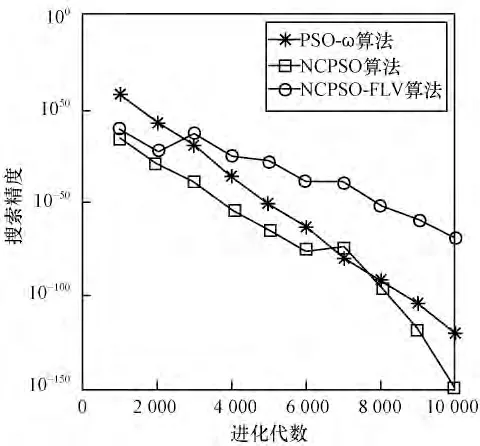
图3 测试函数F3的收敛曲线

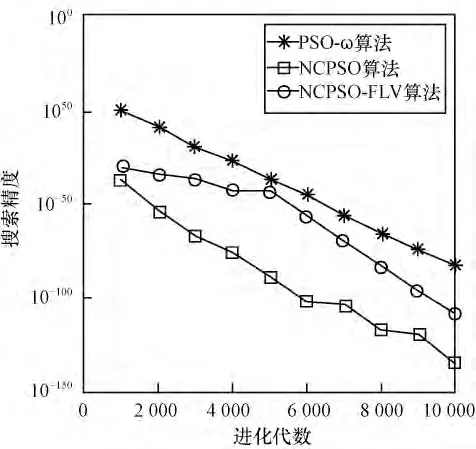
图4 测试函数F4的收敛曲线

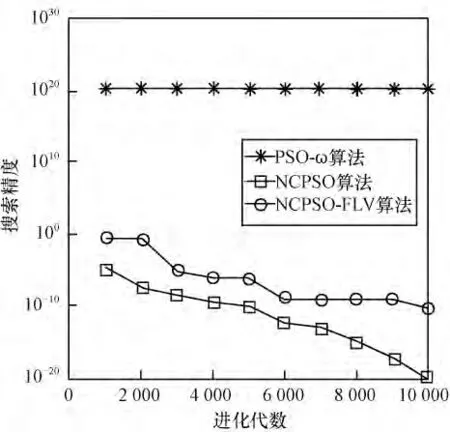
图5 测试函数F5的收敛曲线

由图1～图3 可知，NCPSO-FLV 算法加入速度调节因子之后收敛速度加快，精度提高。对函数F1和F3收敛较快，对于较难最小化的函数F2，NCPSOFLV 算法后期容易陷入局部最优值，但是精度比小生境粒子群算法提高很多。由图4 和图5 可知，对于F4函数，NCPSO-FLV 算法后期收敛速度较慢，但是仍然取得了较好的精度。对于F5，NCPSO-FLV 算法精度较高，而且比小生境粒子群算法的振荡减小很多。

根据以上测试结果，可以得出以下结论:

(1)调节因子小生境粒子群算法比小生境粒子群算法的精度高，从5 个测试函数来看，调节因子小生境粒子群算法最高能够达到1e -100 数量级的精度，远高于小生境粒子群算法。

(2)调节因子小生境粒子群算法在绝大多数测试函数上的后期收敛性能较好。

(3)以算法达到可接受搜索精度作为标准时，调节因子的粒子群算法具有更快的速度。

(4)针对一个固定的搜索精度而言，调节因子的粒子群算法鲁棒性较好。

3.3 实例计算

最优化技术致力于如何解决工程模型，把最优化问题表示为数学模型和如何求最优解。在全球经济一体化的进程中，企业参与全球化生产网络与其他企业建立合作关系分工合作地进行生产与贸易实现互利共赢是经济发展的趋势［11］，在大量零组件需要外部协作实现这种协作性生产的生产模式中，品牌企业如何合理分配订单给不同的代工企业供应商进行生产，即生产任务分配问题就成为这种生产方式的主要决策。在此类任务分配问题中，一方面每个订单的交货期和售价各不相同，另一方面承担这些订单的供应商及其加工成本及加工时间也是各不相同的。针对这些情况，为找到一个最优的订单分配方案就需要考虑成本收益服务水平等目标因素，以最终达到整体的订单效益最大化［12］。

对于企业而言，使得订单效益最大化，就是如何优化生产任务分配问题，其中最重要的环节之一就是如何分配工作单位。工作单位分配，也就是将总任务分配给若干单位，由于各个单位的生产能力和成本不一样，实际上存在一个最有分配的优化问题。

重庆一汽车零件厂共有5 个车间，每个车间的生产能力、单位产品成本、库存原材料总量、单位产品消耗中的原材料如表6 所示。

优化的目标函数自然是成本函数。

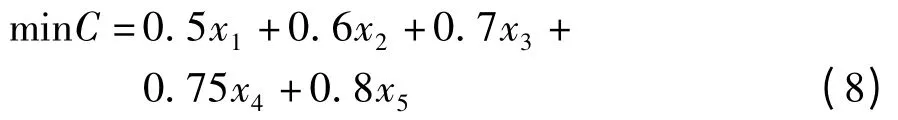
其中，xi为各个车间产品分配量。

限制条件如下:

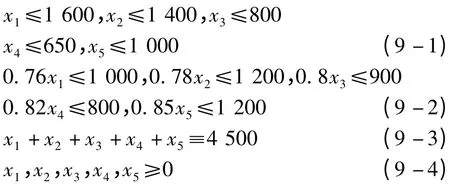
标准结果为:

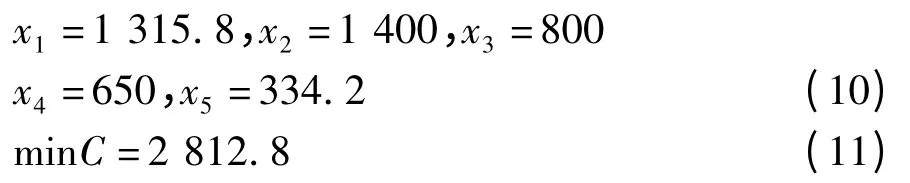
利用NCPSO 的计算结果为:

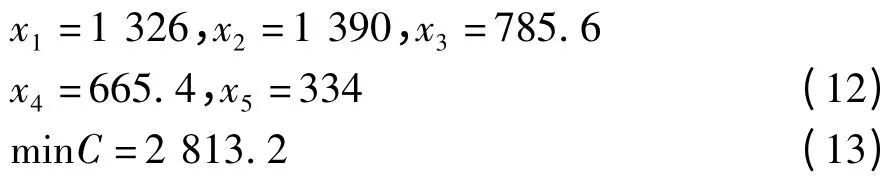
用NCPSO-FLV 的计算结果为:

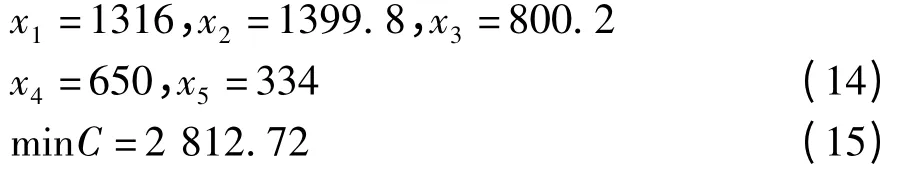
可以看出，调节因子的小生境粒子群算法的计算结果更精确。

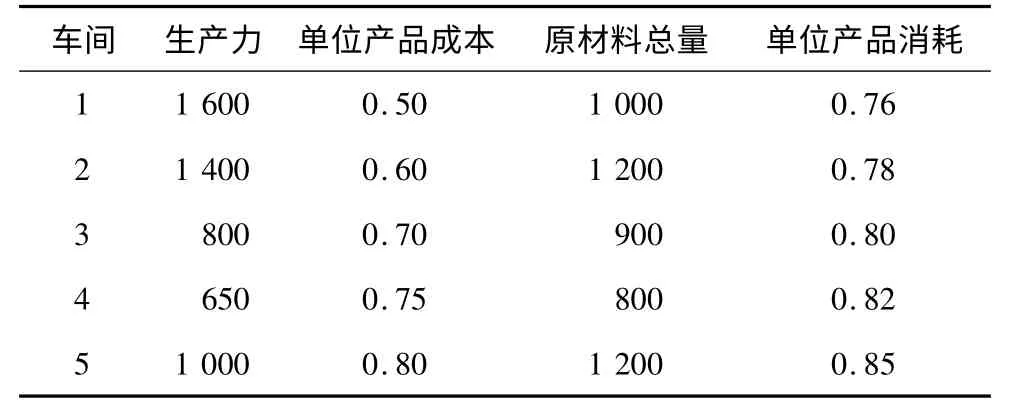
表6 零件厂生产资料信息

3 种算法针对实例的收敛曲线如图6 所示，同样可以看出，NCPSO-FLV 算法的收敛精度最高。

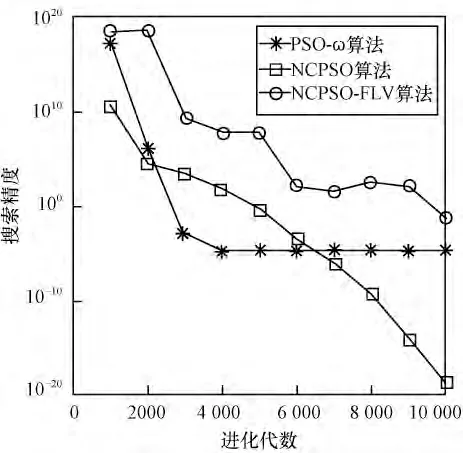
图6 收敛曲线比较

4 结束语

本文提出了一种加入调节因子的小生境粒子群算法，利用小生境种群多样性的概念，在搜索过程中，根据调节因子对粒子速度和位置的不断调整，加强了各个粒子的社会性和粒子的多样性，提高了粒子群的收敛速度和搜索进度。但该算法在个别测试函数上后期收敛速度不是很理想，对其进行改进是下一步的研究方向。

［1］Kennedy J，Eberhart R C.Particle Swarm Optimization［C］//Proc.of IEEE International Conference on Neural Network.Perth，Australia:IEEE Press，1995:1942-1948.

［2］陈国强，王宇平.采用离散粒子群算法的复杂网络重叠社团检测［J］.西安交通大学学报，2013，47(1):107-113.

［3］Brits R，Engelbrchta P，Bergh F D.A Niching Particle Swarm Optimizer［C］//Proc.of IEEE Conference on Simulated Evolutionary and Learning.Singapore:IEEE Press，2002:1037-1040.

［4］史哲文，白雪石，郭 禾.基于改进小生境粒子群算法的多模函数优化［J］.计算机应用研究，2012，29(3):465-468.

［5］宫艳雪，黄 道，孙少超.基于Mamdani 模糊推理系统的制造/再制造混合系统的最优定价［J］.华东理工大学学报，2011，37(6):759-764.

［6］Li Changhe，Yang Shengxiang，Nguyen T T.A Self-Learning Particle Swarm Optimizer for Global Search［J］.IEEE Transactions on System Man and Cybernetics:Part B，2012，42(3):627-645.

［7］韩锦东，李英俊，陈志祥.带能力约束的多目标OEM协作生产订单分配决策与混合蚁群算法应用研究［J］.中国机械工程，2012，23(22):2714-2719.

［8］贾东立，张家树.基于混沌变异的小生境粒子群算法［J］.控制与与决策，2007，22(1):117-120.

［9］Yao Xin，Liu Yong，Lin Guangming.Evolutionary Programming Made Faster［J］.IEEE Transactions on Evolutionary Computation，2004，3(2):82-102.

［10］Clerc M，Kennedy J.The Particle Swarm-Explosion，Stability，and Convergence in a Multidimensional Complex Space ［J］.IEEE Transactions on Evolutionary Computation，2002，6(1):58-73.

［11］谢 康，肖静华，周先波，等.中国工业化与信息化融合质量:理论与实证［J］.经济研究，2012，(1):1-16.

［12］王永瑜，郭立平.绿色GDP 核算理论与方法研究［J］.统计研究，2010，27(11):77-84.