融合影响因子的加权协同过滤算法
高全力,高 岭,杨建锋,王 海,任 杰,张 洋
(西北大学信息科学与技术学院,西安 710127)
1 概述
随着网络的急剧扩张,网络上的资源呈现几何性的增长,包括音频、视频、新闻等充斥着整个网络。这带来了两方面的困扰,一方面是从用户的角度,从海量的资源中找到自己真正感兴趣的资源越来越困难;另一方面是从网络服务提供商的角度,由于用户留给推荐系统有价值的信息非常少,为不同的用户准确地推荐资源也越来越困难。因此,对于高质量推荐系统的需求也就越来越大。
许多研究人员提出了各种推荐算法的思路及其具体的实施方案,例如基于内容过滤的推荐算法[1]、适应性推荐算法[2]、基于项目的推荐算法[3]等。其中,协同过滤算法是目前最成功的推荐算法之一,在电影、歌曲、图书等领域都有广泛的应用,其中在电子商务推荐系统中的成功应用[4]使其受到广泛关注。尽管协同过滤算法非常成功和受欢迎,但它仍有2 个局限性:数据稀疏性和冷启动问题。数据稀疏性指的是在一个庞大的用户空间里只有很少的用户对项目进行评分,这样也就导致了在计算相似度时,所能依赖的信息较少,降低了相似度计算的可信度[5]。冷启动问题分为用户冷启动问题与项目冷启动问题,指的是对于新加入系统的用户或项目系统很难做出高质量的推荐[6]。为了解决这2 个问题,文献[7]等通过分析基于内容的推荐算法与协同过滤推荐算法的优缺点,提出了将两者相融合的推荐算法;文献[4]借鉴社会网络中人与人之间的信任评价方法,提出一种基于信任机制的协同过滤推荐算法,提高了推荐质量;文献[8]通过将联合聚类与协同过滤算法相结合,采用聚类技术解决数据稀疏性;文献[9]通过降低矩阵维数来解决数据稀疏的问题。然而,研究人员在关注于这2 个问题时,却忽视了另一个重要的问题——相似度的计算算法。单纯地使用基于用户或者基于项目或者仅仅将两者简单结合的相似度算法[3-10],具有很大的局限性。首先由于数据集的潜在的稀疏性,可能导致算法计算出的相似性数值差别非常小,进而无法找出真正的相似用户或相似项目。其次没有充分考虑,对任意2 个用户共同评分过的项目个数与任意2 个项目间共同评分的用户个数对相似性计算的影响。
针对上述问题,本文提出种基于影响因子的相似度计算方法。从用户与项目2 种角度来解决相似度的计算问题,把用户间共同评分项目的个数与项目间共同评分用户的个数作为影响因子来修正相似度的计算,并根据2 种相似度计算方法,分别提出了不同的预测评分计算算法。为平滑预测评分,将基于用户的预测评分与基于项目的预测评分进行加权,得到最终预测评分。
2 问题描述
在协同过滤算法中,首先应根据历史数据库建立一个user-item 评分矩阵,矩阵中的各个数值即表示用户对相应项目的评分值,如表1 所示。
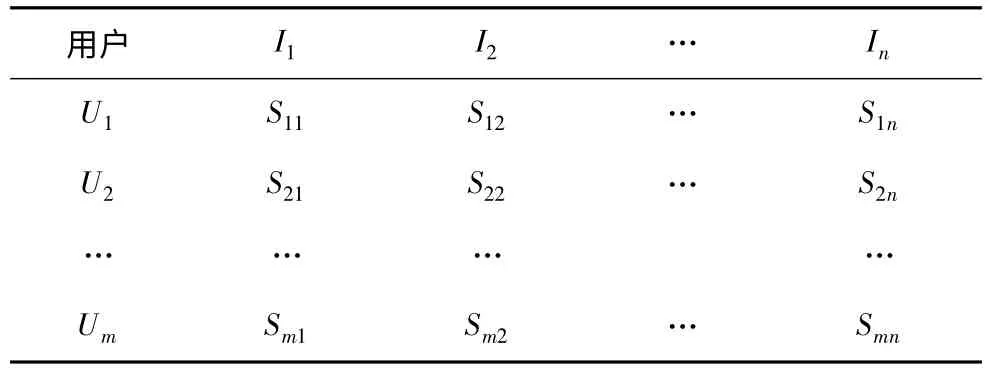
表1 user-item 评分矩阵S(m,n)
其中,表1 共有m 行n 列,分别代表m 个用户与n 个项目;Smn表示用户Um对于项目In的评分值。
然后以评分矩阵为基础,采用基于用户或基于项目的余弦相似度、修正的余弦相似度[1]或者相关相似度[11]来计算用户间或者项目间的相似度的值。并将其作为用户间或项目间的最终相似度。根据相似度的值找出最近邻用户或最近邻项目,以此为基础通过评分算法计算出预测评分。最后根据预测评分的排序序列进行推荐。
在余弦相似度计算方法中,对于用户没有做出评分的项目评分全部置为0 分,在用户空间非常大且数据非常稀疏的情况下,这种假设会极大地影响相似度的计算[12]。在相关相似度的计算方法中,虽然在未评分项目的处理上,采取了一些措施来缓解其带来的影响(在计算用户相似性是采用用户间共同评分的项目作为参评对象),并且通过减去用户对所有项目评分的平均评分来修正不同用户存在的评分偏见。但是这种做法在数据稀疏性的情况下,仍不能有效地计算出实际的相似度[13]。
3 本文算法
在本文的算法中,从用户与项目2 种角度来解决相似度的计算问题,将基于用户间共同评分项目与项目间共同评分用户的影响因子,与修正的余弦相似度的乘积计算用户间及项目间的相似度。并根据2 种相似度计算方法,分别提出不同的预测评分计算算法,即融合影响因子的用户协同过滤算法(Fused Impact Factor of User Based Collaborative Filtering,IFUBCF)、融合影响因子的项目协同过滤算法(Fused Impact Factor of Item Based Collaborative Filtering,IFIBCF)、融合影响因子的加权协同过滤算法(Weighted Collaborative Filtering Based Impact Factor,IFBWCF)。
3.1 融合影响因子的用户协同过滤算法
用户的相似度表示用户间兴趣的重合程度,相似度的计算是协同过滤算法较为关键的环节。选择当前用户a 与任意用户b,用户a 与用户b 已评分的项目集合分别为Ia与Ib,其评分项目集合的并集Iab=Ia∪Ib。在Iab上,用修正的余弦相似度[11]计算用户a 与用户b 的相似度公式如下:
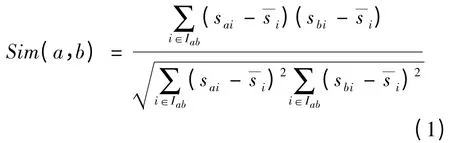
其中,sai表示用户a 对于项目i 的评分;sbi表示用户b 对于项目i 的评分表示项目i 的平均被评分值。由于仅仅根据式(1)得出的相似度的值,有可能会产生一些不准确的情况[13]。例如,2 个用户共同评分的项目较多,但是根据式(1)所得出的相似度的值却有可能较低。并且用户间共同评分项目的个数,是反映用户行为及兴趣重合程度的重要因素。因此,在计算相似度时应充分考虑其对相似度值的影响。所以本文用基于用户间的共同评分项目的个数的影响因子来修正相似度的计算,影响因子βu的计算公式如下:

其中,cab表示用户a 和用户b 之间共同评分过的项目的个数;αu是为了避免式中分母为0 导致无意义或者βu的值为0 导致式(1)中计算出的相似度为0而添加的常数参数;c—u 表示其他任2 个用户共同评分过的项目个数的平均值。由于当用户空间非常大时的值可能会趋于非常小,进而导致βu的值过大,从而使得式(1)中计算的相似度对最终相似度值的影响过低。所以,需要根据不同的数据集调整αu,以修正影响因子的取值。
因此,相似度的最终计算公式为:

为了得到用户a 对于未评分项P 的预测评分,首先根据式(3)中计算的相似度的值,得到其他用户与用户a 的相似度序列,找出用户a 的k 邻近用户。根据k 邻近用户与当前用户的相似度与未评分项目P(P∈Iab)被评分的平均值,通过公式计算出未评分项目P 相对于当前用户a 的预测评分Sa(因为a 为任意用户,为体现一般性,用Susr代替Sa),即IFUBCF 算法,计算公式如下:
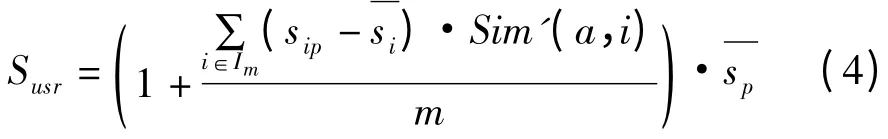
其中,m 为k 邻近用户中对于未评分项目P 有评分的用户的个数,显然1≤m≤k,Im即为此m 个用户空间即为用户i 对于项目P 的评分为用户i 平均评分值为项目的P 的平均评分。则基于用户相似度的预测评分即体现为:k 邻近用户对于未评分项的评分与该用户评分均值偏差的和,与其相对于当前用户相似度的乘积对于未评分项平均评分的影响。
3.2 融合影响因子的项目协同过滤算法
项目的相似度表示项目间的相似程度,对任意项目i 评过分的用户集合为Ui,对项目j 评过分的用户集合为Uj,其评分用户并集Uij=Ui∪Uj。在Uij上用基于项目的修正余弦相似度[11]来计算项目i 与项目j 之间的相似度,公式如下:
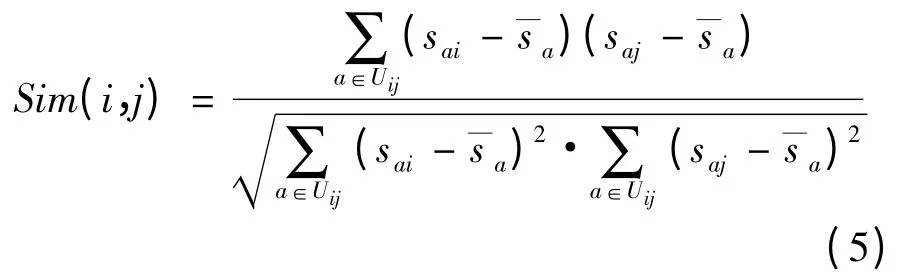

其中,cij表示对项目i 和项目j 共同评分用户的个数表示其他任意2 个项目间共同评分用户个数的平均值;αi为修正β 的常数参数。其最终相似度计算公式如下:

根据式(7)所得出的相似度序列,计算出项目P的k 邻近项目,从而得出用户a 对于未评分项目P的预测评分(因为P 为任意项目,为体现一般性,用Sitem来代替Sp),即IFIBCF 算法,计算公式如下:
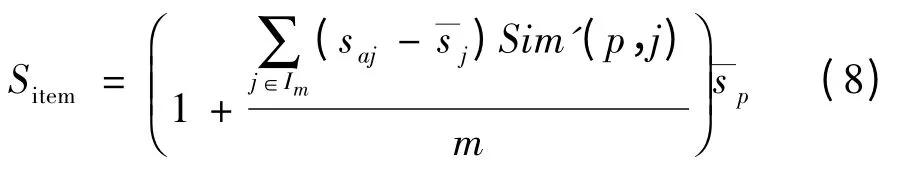
3.3 加权的协同过滤算法
用户与项目作为影响整个推荐系统推荐质量的2 个重要因素,单独选择其中一个作为预测评分的主要基准,是不合理的[14]。因此,本文将2 种算法结合起来,通过引入加权系数,平滑2 种情况下的预测评分,使预测评分更加合理与精确。具体做法是,将基于用户的k 邻近用户中对于未评分项有评分的个数m 与基于项目的k 邻近项目中相对于当前用户被评分项目的个数n 做为加权系数,得出基于影响因子的加权协同过滤算法IFBWCF,即:

其中,Susr表示根据IFUBCF 算法计算出的预测分值;Sitem表示根据IFIBCF 算法计算出的预测分值。根据式(9)计算出当前用户对于未评分项目的最终预测评分,根据TopN 算法为当前用户推荐得分最高的N 个项目。
4 实验结果与分析
实验所采用的PC 机的配置为Intel(R)Core(TM)i5 2.8 GHz CPU,4 GB 内存,操作系统为Windows XP,算法使用Matlab 实现。
4.1 数据集与实验方案
本文中所做实验采用的数据集为MovieLens 数据集,此数据集是常用的基于Web 的衡量推荐算法质量的数据集。对每个电影采取5 分制的评分策略。本文选取的是其公开的一部分数据,包括943 个用户对于1 682 部电影的100 000 条评分记录。其中,每个用户都至少对20 部电影进行了评分。分数的数值越高表示用户对于这部电影的喜爱程度越高。为缓解采用单一数据集导致的实验结果缺乏说服力,本文采用All But One 算法对数据集进行处理。并将数据集分为训练集与测试集两部分,在最近邻居k 值的选取对推荐结果的影响上,将本文算法与多类属概率潜在语义的协同过滤算法PLSA(Probabilistic Latent Semantic Analysis)[9]相对比。
4.2 算法的评价标准
一般来说,评价一个推荐算法质量的标准有统计精度度量方法和决策支持精度度量方法。本文实验所采用的是属于统计精度度量方法的平均绝对误差(Mean Absolute Error,MAE)[11]作为检验推荐算法的标准。MAE 通过预测的用户评分与实际的用户评分之间的偏差来度量预测的准确性。算法的MAE 越小表明算法的预测越准确,意味着算法的推荐质量越高。设预测用户评分的集合表示为{p1,p2,…,pN},对应的实际用户评分集合为{q1,q2,…,qN},则:

4.3 算法的复杂度分析
一个算法质量的优劣将直接影响到算法乃至整个程序的效率,为了检验算法性能与改进算法,需对算法进行复杂度分析。在本文所描述的3 种算法中,算法的时间复杂度主要由两部分组成:计算相似度矩阵与找出k 邻近用户或项目并计算预测评分所需的时间来决定的。假设某数据集中,用户数为m,项目数为n。在IFUBCF 与IFIBCF 算法中,计算相似度矩阵的时间复杂度分别为O(m2n)与O(mn2)。在IFBWCF 算法中则为O(m2n)+O(mn2)。在IFUBCF 与IFIBCF 算法中,时间复杂度分别为O(mn2)与O(m2n)。在IFBWCF 中为O(m2n)+O(mn2)。所以,在用户数大于项目数的情况下,3 种算法的时间复杂度分别为O(m2n)、O(mn2)与O(m2n),否则分别为O(mn2)、O(m2n)与O(m2n),与传统的User-based 协同过滤算法(O(mn2))和Item-based 协同过滤算法(O(m2n))基本一致。
4.4 参数的取值分析
由于本文对于数据集采用All but one 算法进行处理,即每次评分数据的隐藏都是随机的,相当于每次进行运算的数据集都在变化,这也必然导致根据评分算法得出的预测评分的上下浮动。因此,本文对于α 值的选取采用在每个节点计算5 次,然后取其均值。本次实验中在选取不同邻居点数目情况下,分别使α取0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0 对3 种算法进行测试,以便求出使各算法最优的α 值。α 值对3 种算法影响的实验结果如图1~图4 所示。
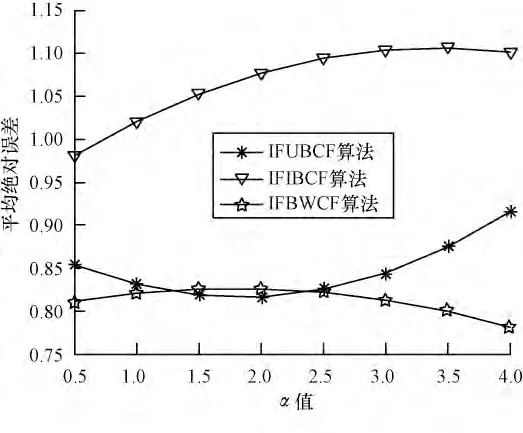
图1 最近邻居数为10 时α 对算法的影响
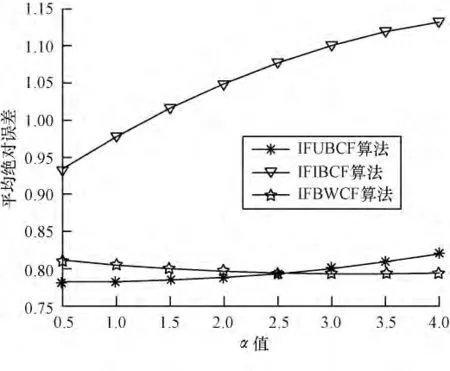
图2 最近邻居数为20 时α 对算法的影响
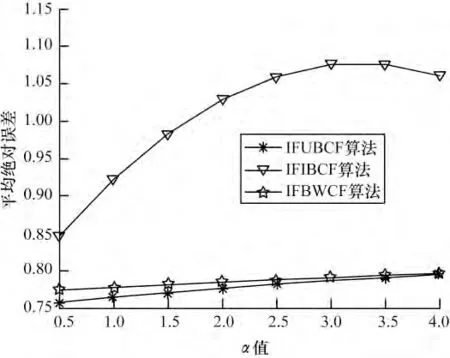
图3 最近邻居数为30 时α 对算法的影响
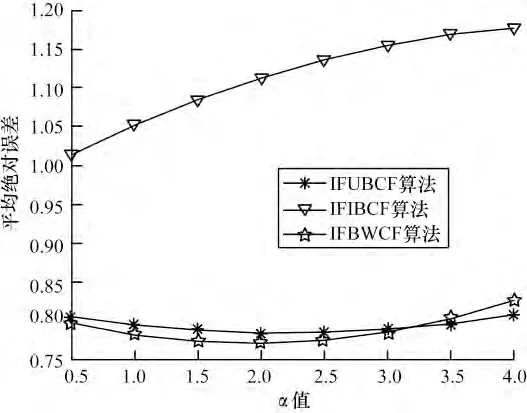
图4 最近邻居数为40 时α 对算法的影响
可以看出,随α 值的增加:图1 中IFIBCF 算法与IFUBCF 算法呈递增趋势,IFWBCF 算法呈递减趋势,在1.0 与1.5 处,3 个算法总体MAE 最小;图2 中IFIBCF 算法呈递增趋势,IFUBCF 算法在1.5~2.0 间取得最小值,IFWBCF 算法在2.5 以后逐渐下降;图3表明3 个算法在1.0~1.5 间总体MAE 最小;图4 中3个算法都呈递增趋势α 值越小,总体MAE 越好。分析可得,当α 取1 时,3 种算法的总体MAE 值较小,也即3 种算法在此时预测评分最准确。因此,本文对算法进行评价性测试时,α 统一为1。
4.5 算法分析
通过对PLSA 算法与本文所给出的3 种算法进行试验对比,从数据集中随机抽取98 个用户的评分数据。对于这些数据采用All But One 算法进行隐藏处理,然后对这些被隐藏评分的项目进行预测评分。最后计算预测评分与实际评分的偏差值,通过MAE 的值来度量预测评分的准确度。在最近邻居数分别选取5,10,15,20,25,30,35,40 时分别运行IFUBCF、IFIBCF、IFBWCF、PLSA 算法,对每个算法在各邻居点分别运行5 次取其均值。实验结果如图5所示。
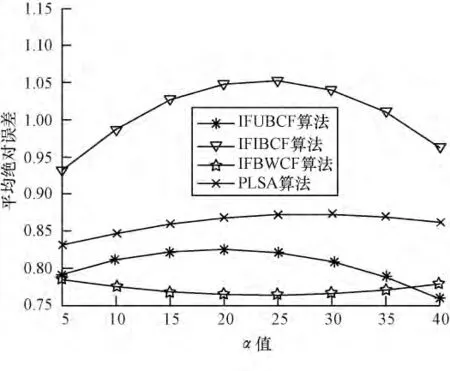
图5 各协同过滤算法的对比
实验结果表明,本文提出的基于影响因子的加权协同推荐算法与其他算法相比,具有较小的MAE值,推荐的准确度较高,能够获得更好的推荐质量。
5 结束语
本文从基于用户与基于项目2 个角度对协同过滤算法进行改进,在计算用户相似性时,考虑了用户间共同评分项目的个数对于相似性的影响。在计算项目相似度时,考虑对项目有共同评分的用户的个数对于相似度的影响。这种方法增加了相似度计算的合理性,使得对于未评分项的预测更为准确。并且在这2 种改进算法的基础上,提出一种基于影响因子的加权协同过滤算法,能更加客观地把2 种情况下的预测评分综合起来平滑2 种情况下的得分,使得预测评分能够更加接近实际得分值,进而获得更好的推荐质量。下一步将研究一种能够根据不同用户的选择自动修正评分算法的新方法,以进一步提高算法的推荐质量与智能性。另外,基于海量数据的推荐算法优化也是今后一个重要的研究方向。
[1]胡福华,郑小林,干红华.基于相似度传递的协同过滤算法[J].计算机工程,2011,37(10):50-51,54.
[2]Shahab I C,Chen Y S.An Adaptive Recommendation System Without Explicit Acquisition of User Relevance Feedback[J].Distributed and Parallel Databases,2003,14(2):173-192.
[3]Deshpande M,Karypis G.Item-based Top-n Recommendation Algorithms[J].ACM Transactions on Information Systems,2004,22(1):143-177.
[4]夏小伍,王卫平.基于信任模型的协同过滤推荐算法[J].计算机工程,2011,37(21):26-28.
[5]Papagelis M,Plexousakis D,Kutsuras T.Alleviating the Sparsity Problem of Collaborative Filtering Using Trust Inferences[M].Berlin,Germany:Springer,2005.
[6]Lam X N,Vu T,Le T D,et al.Addressing Cold-start Problem in Recommendation Systems[C]//Proceedings of the 2nd International Conference on Ubiquitous Information Management and Communication.[S.1.]:ACM Press,2008:208-211.
[7]Melville P,Mooney R J,Nagarajan R.Content-boosted Collaborative Filtering for Improve Recommendations[C]//Proceedings of National Conference on Artificial Intelligence.London,UK:MIT Press,2002:187-192.
[8]George T,Merugu S.A Scalable Collaborative Filtering Framework Based on Co-clustering[C]//Proceedings of the 5th IEEE International Conference on Data Mining.Texas,USA:IEEE Press,2005:4.
[9]侯翠琴,焦李成,张文革.一种压缩稀疏用户评分矩阵的协同过滤算法[J].西安电子科技大学学报,2009,36(4):614-618.
[10]Chun Zeng,Xing Chunxiao,Zhou Lizhu.Similarity Measure and Instance Selection for Collaborative Filtering[C]//Proceedings of the 12th International Conference on World Wide Web.Budapest,Hungary:ACM Press,2003:652-658.
[11]汪 静,印 鉴,郑利荣,等.基于共同评分和相似性权重的协同过滤推荐算法[J].计算机科学,2010,37(2):99-104.
[12]Sarwar B,Karypis G,Konstan J,et al.Item-based Collaborative Filtering Recommendation Algorithms[C]//Proceedings of the 10th International Conference on World Wide Web.USA:ACM Press,2001:285-295.
[13]Massa P,Avesani P.Trust-awareCollaborative Filtering for Recommender Systems [M].Berlin,Germany:Springer,2004.
[14]Ghazanfar M,Prugel-Bennett A.NovelSignificance Weighting Schemes for Collaborative Filtering:Generating Improved Recommendations in Sparse Environments[C]//Proceedings of 2010 International Conference on Data Mining.[S.1.]:IEEE Press,2010:215-223.

