基于GPU的SAS成像算法并行实现研究＊

（海军工程大学电子工程学院 武汉 430033）

1 引言

合成孔径声纳（Synthetic Aperture Sonar，SAS）是一种高分辨率水下成像声纳，基本原理是［1～3］：利用小尺寸基阵沿空间匀速直线运动来合成大孔径基阵，获得不依赖于距离和波长大小的高方位向分辨率图像。SAS被广泛应用在海底地形测绘、海洋地质考察、沉底物打捞以及水雷的探测和识别。随着SAS成像技术的发展和实际应用需求，对回波数据实时处理的要求也越来越迫切。由于SAS成像算法本身的复杂性和数据量大，传统的处理方式难以满足实时成像的要求，采用并行技术是实现高性能SAS成像的必经之路。文献［4］中指出，RD［5］算法能够兼顾成熟、简单、高效和精确等因素，至今仍是使用最广泛的成像算法。本文首先给出了多子阵［9］合成孔径声纳的RD算法，然后研究了基于GPU 的RD成像算法的并行处理方法。

2 多子阵RD 算法简介

假定发射信号为线性调频信号，易知多子阵合成孔径声呐第i个接收阵在距离为r处的点目标的回波信号基带形式［9］可写为

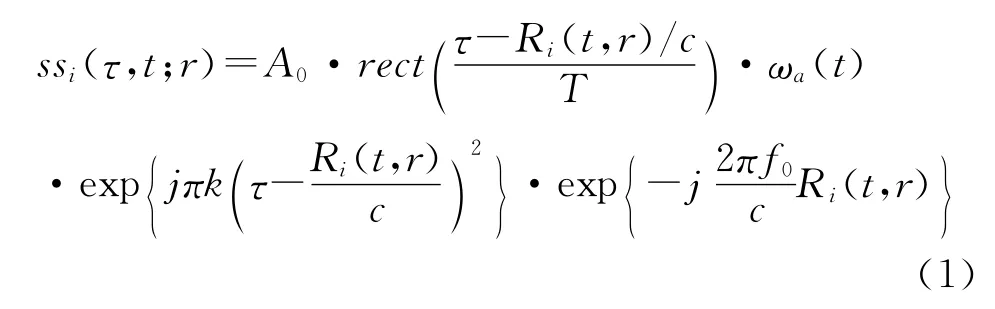
式中A0为幅度函数，可视为常数，ωa（·）为方位向包络函数，k为发射信号调频斜率，c为声速，f0为信号中心频率，R0（t，r）为延时距离误差。

首先对式（1）距离向快变时间和方位向慢变时间作傅立叶变换，进入fr-fa域：

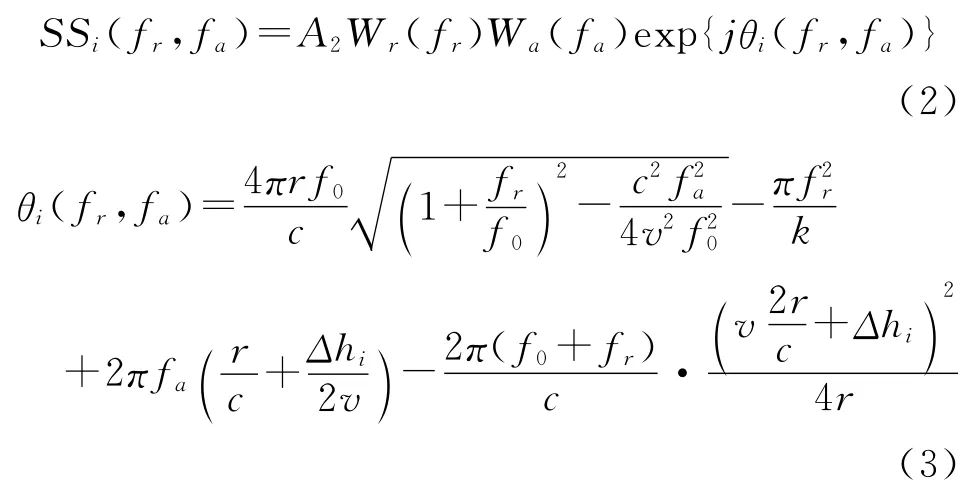
其中A2为常数，Wr（·）为距离频谱包络，Wa（·）为方位频谱包络，fr为距离向瞬时频率，fa为方位向瞬时频率，Δhi表示为第i接收子阵中心与发射阵中心的间距。

将上述公式中的根式对fr做泰勒展开并舍弃二次以上项［8］并作距离向进行反傅立叶变换，进入RD 域：

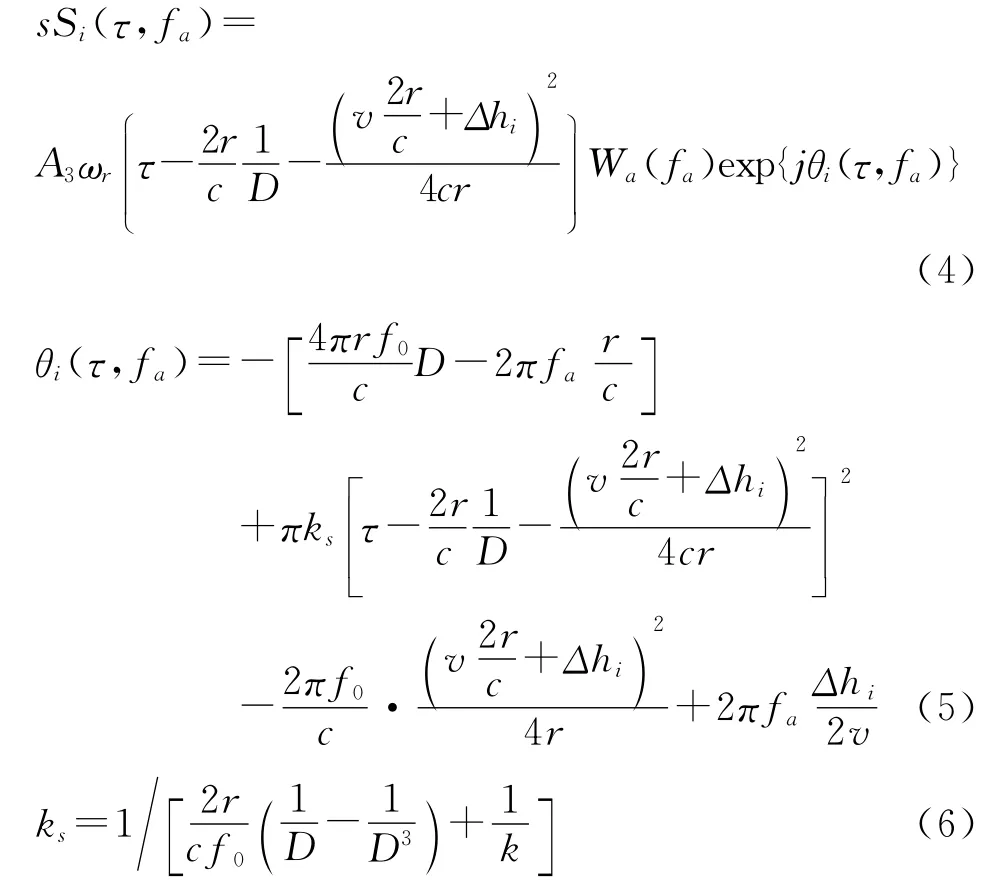
这里ks为距离多普勒域新的距离调频率，D＝

从式（5）中可以发现，第一项为方位调制项，它包含两部分内容：方位脉压函数φa1和方位走动函数φa2。

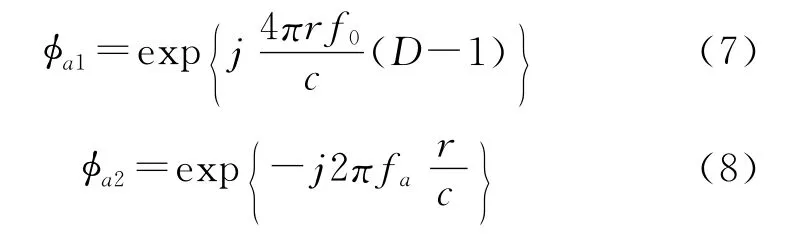
第二项为距离弯曲项，时间徙动量为Δτ：

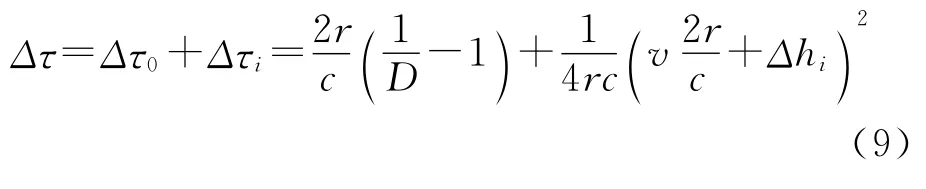
其中Δτi为停走停近似及各个接收阵接收路径不同造成的延迟误差，与方位向无关，因而可以在距离脉压后的回波数据中分别予以补偿。

式（5）第三项为停走停近似及不同接收阵引入的固定相位φi，也与方位向无关，也可以在各接收阵回波数据中分别予以补偿。

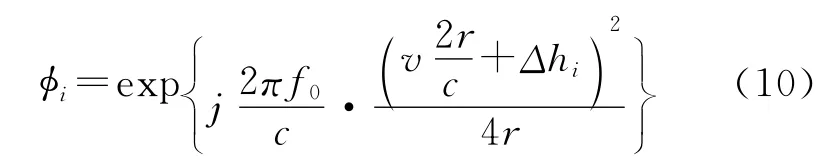
式（5）最后一项为只与各接收阵的方位位置有关的相位项，其物理意义可表征为各接收阵数据方位向的间隔为Δhi／2顺序排列。

至此完成了多接收阵的距离多普勒算法，其流程图如图1所示。

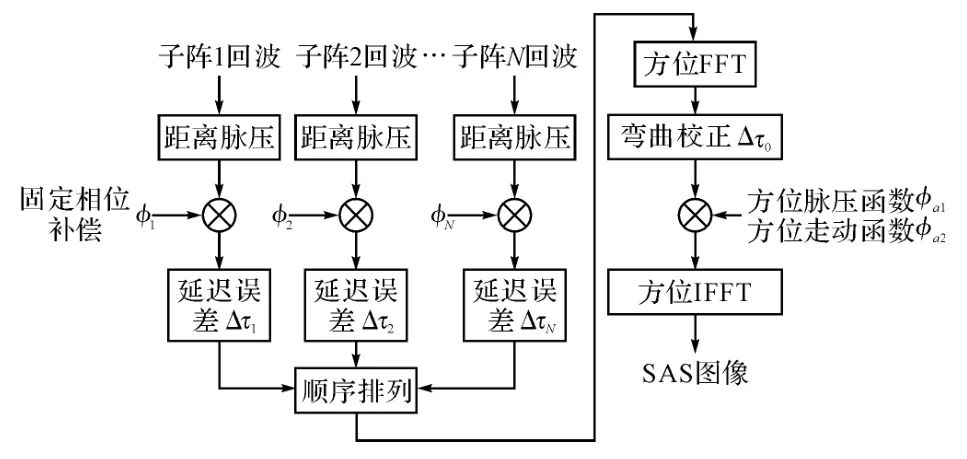
图1 多接收阵RD 成像算法流程图

3 基于CUDA的GPU 并行技术简介

CUDA 采用了统一处理架构，降低了编程的难度，并且NVIDIA GPU 引入了片内共享存储器，提高了效率。这两项改进使CUDA 架构更加适合进行GPU 通用计算。CUDA 中线程按照两个层次进行组织、共享存储器和栅栏同步［6］。这些关键特性使得CUDA 拥有了两个层次的并行：线程级并行实现的细粒度数据并行，任务级并行实现的粗粒度并行。

CUDA编程模型是将CPU 作为主机端（Host），将GPU 作为设备端（Device），同时在一个系统中可以存在一个主机和多个设备或者多个主机和多个设备［7］，即GPU 集群。CUDA 程序的核心是内核（Kernel）函数，其在设备端执行并通过主机端调用，主要任务是完成数据的并行处理。一个完整的CUDA程序是由若干个运行在Device端的Kernel函数并行处理步骤和Host端的串行处理步骤共同组成。在主机端调用时需要设置内核函数的执行参数。执行参数设置主要是指线程块、线程网格维度的设计、共享存储空间的分配以及流的设计等。

4 RD 算法的GPU 并行实现

本文选择RD 算法进行SAS的成像［9］，首先对距离进行脉冲压缩，再进行距离徙动校正，然后进行方位向脉冲压缩。距离脉压和方位脉压在这里使用频域匹配滤波实现，主要涉及的是傅里叶变换、向量和矩阵的点乘和逆傅里叶变换。在CUDA中包含了CUFFT 库，可以利用CUFFT 库实现傅里叶变换［10］和逆傅里叶变换在GPU 上的并行计算。然后，通过编写的核函数实现向量和矩阵的点乘和转置运算。具体算法流程如图2所示。

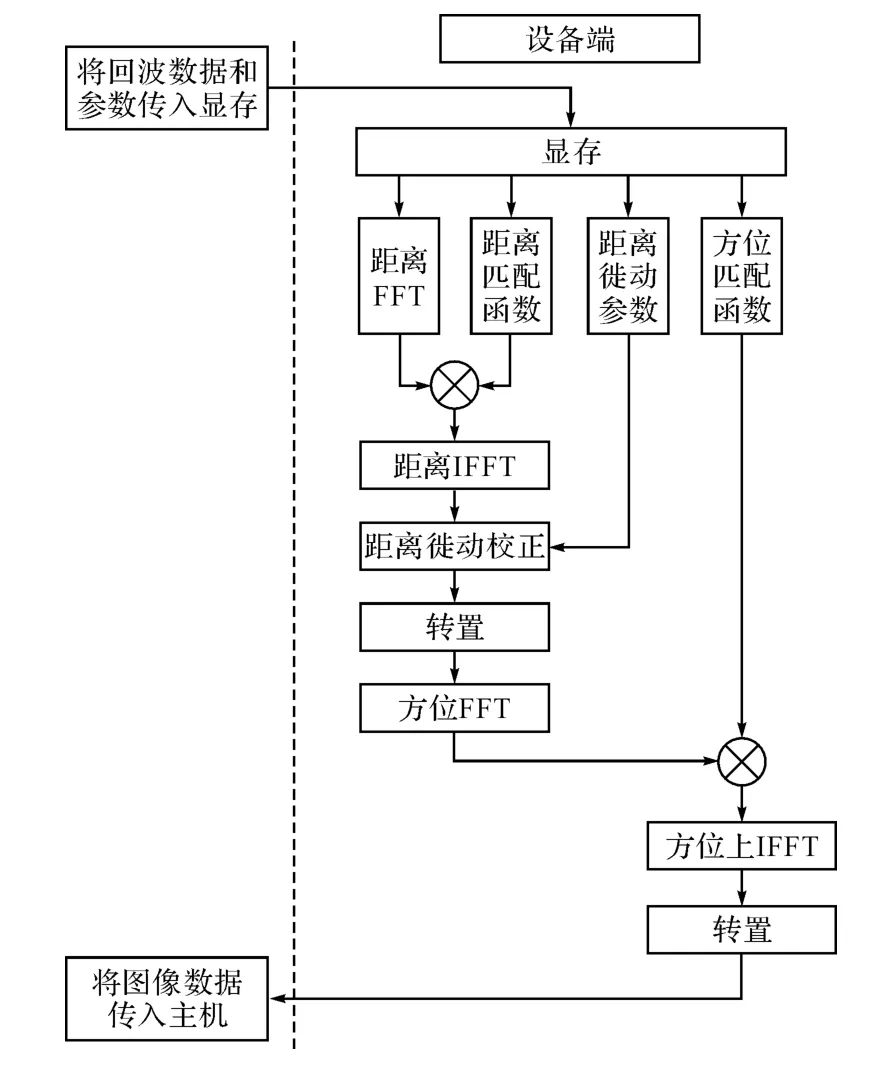
图2 基于CUDA 的RD 成像并行算法流程图

利用CUDA开发的RD成像算法实现流程如下：

1）将回波数据和参数传入到显存。

2）调用CUFFT 库实现距离向的傅里叶变换并行运算，同时计算距离匹配函数、方位匹配函数和距离徙动参数。

3）编写的点乘核函数实现距离向数据和距离匹配函数的点乘，然后调用CUFFT 库并行实现距离向的逆傅里叶变换，完成距离向脉冲压缩。

4）利用距离徙动参数在GPU 上实现距离徙动校正，然后用核函数实现数据的并行转置。

5）调用CUFFT 库实现方位向数据的傅里叶变换，然后用点乘核函数实现与方位匹配函数的点乘，最后调用CUFFT 库并行实现方位向的逆傅里叶变换，完成方位向脉冲压缩。

6）将图像数据传回主机端。

5 实验与结果

为了验证本文所提出的SAS成像方法的有效性，本文进行了五个点的SAS 成像仿真实验。本实验采用的计算机CPU 为Intel（R）G840CPU 双核2．8G，内存4G，显卡为GeForce 210，显存为1G，运算能力为1．2，运算精度为单精度。软件使用的是Windows XP下的CUDA 4．0．和VS2008。数据来源于合成孔径声纳接收回波的计算机仿真。仿真参数如表1所示。

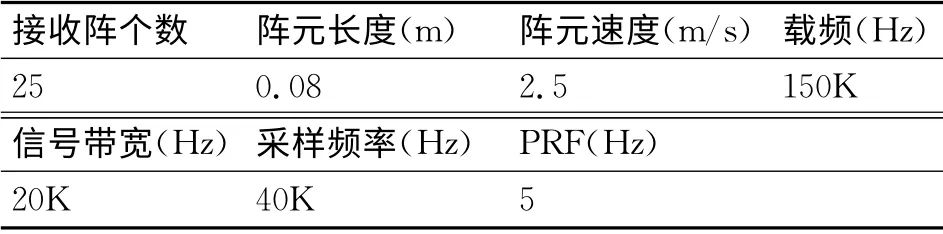
表1 SAS信号仿真参数

针对不同数据大小的回波，在CPU 和GPU 上分别进行RD成像仿真效率的比较，其结果如表2所示。

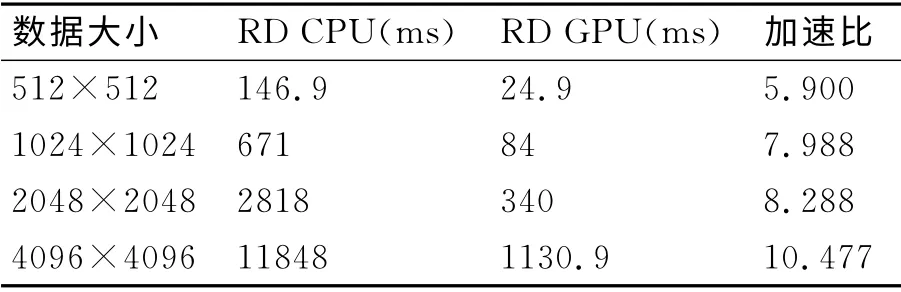
表2 CPU 和GPU 上RD 算法效率比较

从表2的计算效率比较结果可以看出，随着原始回波数据量的增加，并行RD 算法的加速比也在逐步增加，可见对于高维数的SAS回波，更能够体现并行算法的优势。

图3和图4分别是RD 算法在GPU 和CPU上局部放大后的1024×1024个复数成像的结果。

图3 GPU 成像结果

图4 CPU 成像结果

从图3和图4可以看出，基于GPU 的仿真结果和基于CPU 的仿真结果在成像结果上的一致性，但是从表2可以看出两者的运算速度却有明显的差距。

由测试的结果可以知道，基于GPU 的RD成像算法，具有较高的效率，能够满足实时成像的要求。

6 结语

本文设计了基于GPU 的SAS成像并行算法，并对该并行成像算法进行了计算机仿真，验证了算法的可行性和高效性。实验结果表明，基于CUDA开发出来的SAR 成像并行算法，实现了实时成像，可满足下一步处理的需要。

［1］张学波，唐劲松，张森，等．多接收阵合成孔径声纳线频调变标成像算法［J］．系统工程与电子技术，2013，35（7）：1415-1420．

［2］张学波，唐劲松，钟何平．合成孔径声纳多接收阵数据融合CS成像算法［J］．哈尔滨工程大学学报，2013，34（2）：240-244．

［3］杨海亮，张森，唐劲松．宽测绘带多接收阵合成孔径声纳成像处理方法［J］．系统仿真学报，2011，23（7）：1424-1428．

［4］禹卫东．合成孔径雷达信号处理研究［D］．南京：南京航空航天大学博士论文，1997．

［5］保铮，邢孟道，王彤．雷达成像技术［M］．北京：电子工业出版社，2006．

［6］张舒，诸艳利．GPU 高性能运算之CUDA［M］．北京：水利水电出版社，2009．

［7］桑德斯（美）．GPU 高性能编程CUDA 实战［M］．聂雪军，等译．北京：机械工业出版社，2011．

［8］Cumming I G，Wong F H．合成孔径声纳雷达成像-算法与实现［M］．洪文，等译．北京：电子工业出版社，2007，10．

［9］杨海亮．多接收阵合成孔径声纳成像算法研究［J］．博士论文．海军工程大学，2009．

［10］赵丽丽，张胜兵，张萌，等．基于CUDA 的高速FFT 计算［J］．计算机应用研究，2011，28（4）：1556-1559．