EMD在海洋内波研究中的应用＊

（海军潜艇学院 青岛 266071）

1 引言

内波过程是非线性的，对其观测资料进行的处理分析往往是建立在一些必要假定的基础上［1］。在对内波资料进行处理分析的过程中，如果能尽量减少对假定性条件的依赖，在实际应用中就很有意义。黄锷提出了一种新的数据处理方法—经验模分解方法［2～4］，它的特点是能够对非线性、非平稳过程的数据进行线性化和平稳化处理，并在分解的过程中保留了数据本身的特性，再对各分量进行Hilbert变换，得到各自的瞬时频率和瞬时振幅，而瞬时振幅在频率—时间平面上的分布就是Hilbert谱，Hilbert谱在客观性和分辨率方面都具有明显的优越性。与此同时，它也解决了非线性、非平稳过程数据距平值变量的求取问题［5～6］。而对于实测内波波动资料中内波信息的提取，通常采用滤波的方法，对于内波垂向模态，以往多为通过方程解算得到，而通过实测数据获取垂向模态目前并没有较实用的方法［7～10］。

2 采用数据描述

实验时间为2010年6月30日到7月6日，实验地点为E111°12′，N19°30′，实验仪器为温度链与CTD。温度链共18个探头，其中两个深度探头，16个温度探头，采样频率为1min，从海表至海底16个温度探头对应深度为10m、18m、20．5m、23m、28m、33m、38m、43m、48m、53m、58m、63m、68m、73m、75．5m、81m、89m。CTD测量是利用实验船侧边小吊勾吊CTD入水测取垂向温盐密剖面，采样间隔为1m，采样频率为1h，因跃层处的温度波动最明显，我们取跃层深度处的温度波动，如图2所示。

3 基于EMD 分解方法的内波温度波动分析

取此次测量过程中一次明显的内波过程，图1为2010年7月2日4点到11点的温度等值线图，其中横轴为时间，纵轴为深度，从图中可以看出明显的内波波动。

图2为取整个内波过程时间范围内各测层温度的时间平均为该测量点未产生内波时的海水温度值，即平衡位置时的温度。

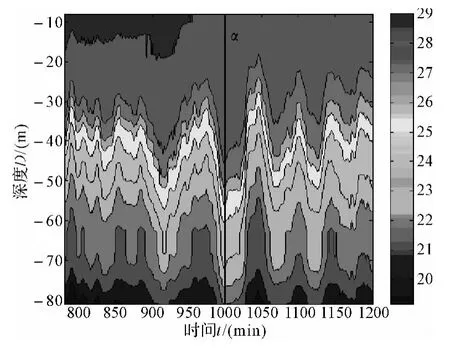
图1 2010年7月2日温度等值线图

图3中，图3（a）为跃层处温度随时间波动图，图3（b）～图3（g）为内波波动EMD 分解的六个模态，图3（h）为EMD 分解的余项。

图2 跃层处温度等值线图

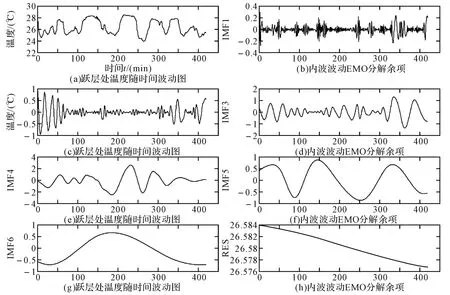
图3 海洋内波温度波动及其EMD 分量IMF与余项

余项表示的是整个温度波动的大趋势，从图3（h）中可以看出，整个波动过程中温度的整体趋势为下降的，观测时间段内，从4 点～11 点的过程中，天气转阴，海面风力加大，海面温度降低，水体的温度整体降低，这与实际相符。

摒除高频部分的干扰，采用正弦曲线逼近与fourier曲线逼近两种方法，对低频模态IMF4、IMF5、IMF6和余项进行函数拟合并叠加，图4为IMF4、IMF5、IMF6和余项的拟合函数叠加构造的波动函数与原温度波动的对比，其中红色线为拟合的波动函数，蓝色线为原温度波动曲线。

介于直接对原温度波动进行拟合的难度，采取EMD 分解后，对低频模态分解并叠加的方法能较好地解决这一问题，且从图4中可以看出，其拟合的效果较好。

4 基于EMD 分解方法的内波垂向模态获取

4．1 垂向位移的求取方法

图5中红线为沿图1中a线由海表至测深底层截取的温度垂向分布，蓝线表示图2中相应时刻平均温度从海表至海底的垂向分布，在图6中选取蓝线上的b点，其深度为h1，其对应的相对于平衡点的温度波动深度为图中黑线对应的坐标轴点c，记深度为h2，则b点对应的内波垂向位移即为h1～h2，对垂向上各个测深点做相应的计算，可以得到垂向上的位移分布如图6a所示。

4．2 应用EMD 方法获取垂向模态函数

对图6a的垂向位移分布EMD 分解，其余项部分表示位移在垂向上的变化趋势，将余项部分归一化，所得的图6d即为内波在该时刻该测点的垂向模态函数，由于测深并未沿至海底，垂向模态函数只表示到测深80m 左右。

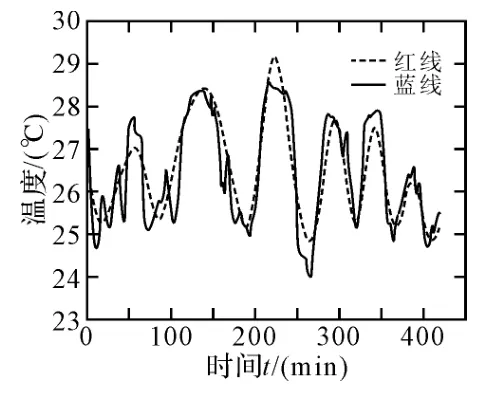
图4 各模态拟合函数叠加图

图5 截取时间点的垂向温度分布与平均温度垂向分布对比

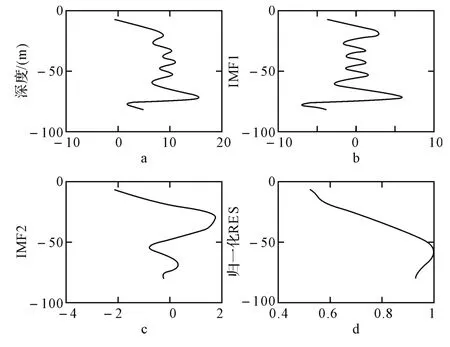
图6 海洋内波垂向位移分布及其EMD分量IMF与余项

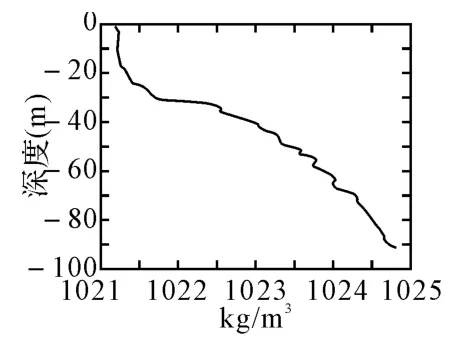
图7 测点的垂向密度分布

图8 根据密度计算所得的垂向模态函数

图7为图1a线时刻CTD 同步测得的垂向密度分布，图8为根据图7的密度分布计算得到的第一模态的垂向模态函数，通过对比图8和图6（d），两者存在很高的一致性，进一步验证了上述求取垂向模态函数方法的有效性。

5 结语

本文从EMD 方法入手，对内波引起的温度时间波动进行了分析，采用对低频模态的拟合，构造出了温度时间波动的函数，经对比与原温度波动相似度较高。采用了一种新的根据实测温度链数据利用EMD 方法获取内波垂向模态的新思路，经实测CTD 密度数据计算验证，该方法获得的经验模态函数有效性较高。

由于该方法计算量较大，所以目前的计算量还无法覆盖全部的观测数据，下一步要加大计算量，对观测到的内波数据进行批量的计算，充分验证上述的两个方法。

［1］方欣华，杜涛．海洋内波基础和中国海内波［M］．青岛：中国海洋大学出版社，2005：159-205．

［2］Norden E，Huang Z S，Steven R，Long，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］．Proceedings of the Royal Society of London．Series A：Mathematical，Physical and Engineering Science，1998，454：899-995．

［3］Huang W，Shen Z，Huang N E，et al．Eng ineering Analysis of Biological Variables：An Example o f Blood Pressure Over 1Day［J］．Proceedings of the National Academy of Sciences，1998，95（9）：4816-4821．

［4］Huang N E，Wu M L，Qu W D．A pplicafions of Hilbert-Huang Transform to Non-Stationary Finaneial Time Series Analysis［J］．Applied Stochastic Models in business and industry，2003，19（3）：245-268．

［5］Li Yu-jun，Peter W Tse，Yang Xin，et al．EMD-Based Fault Diagnosis for Abnormal Clear ance Between Contacting Components in a Diesel Engine［J］．Mechanical Systems and Signal P rocessing，2010，24（1）：193-210．

［6］李卿，张国平，刘洋．基于EMD 的拉曼光谱去噪方法研究［J］．光谱学与光谱分析，2009，29（1）：142-145．

［7］Small J，Hallock Z，Pavey G，et al．Observations of large amplitude internal waves at the Malin Shelf edge during SESAME 1995［J］．Continental Shelf Research，1999，19（11）：1389-1436．

［8］Ramirez C，Renouard D．Generation of internal waves over a shelf［J］．Dynamics of atmospheres and oceans，1998，28（2）：107-125．

［9］T．Kubota D R S K，Dobbs L D．Weakly-nonlinear，long internal gravity waves in stratified fluids of finite depth［J］．Journal of Hydronautics，1978，12（4）：157-165．

［10］Henyey F S，Wright J，FlattéS M．Energy and action flow through the internal wave field：An eikonal approach［J］．Journal of Geophysical Research：Oceans（1978-2012），1986，91（C7）：8487-8495．