测试系统中波形的神经网络识别方法＊

曾 翔 姜本清 徐 涛

（1．海军航空工程学院研究生管理大队 烟台 264001）（2．海军航空工程学院电子信息工程系 烟台 264001）

1 引言

在测试系统中，经常需要测量不同器件输出的各种信号波形，可以说这是测试系统的基本任务之一。测量得到的直接结果是波形数据，测试系统利用这些数据与模板库中的标准参数进行比较，以判定该被测对象工作是否正常，而在计算波形参数之前首先要判定波形的形状，因此波形识别方法的研究是测试系统研究的一个重要方向。

关于波形识别的方法，通常分为两大类。一类方法通过分析信号波形时域特征，从而进行波形模板匹配识别，即对某一待测波形提取其时域特征参数与预测输出的标准模板波形进行对齐、比较和匹配判断。计算待测波形与模板波形的最大相关系数是目前最常用的经典算法（MCC 算法），通过验证发现这种方法存在对波形差异不够敏感的问题；文献［5］针对这一不足提出了一种改进的模板匹配算法，称之为最大相关差值法（MCD 算法），此方法缺点在于要求被检信号的幅值或宽度不能超过模板信号的两倍，否则相关系数将大于1；文献［6］提出用Hausdroff距离度量波形的相似度，在此过程中对度量时分界点的选择有严格的要求，诸如此类方法在处理过程中都需要进行待测波形与模板波形的“对齐”，不利于自动检测系统所要求的快速高效识别，且如果将此类方法应用于测试系统波形的自动识别中，显然会使存储的模板值太多。另一类方法通过分析提取波形频域特征以识别待测波形，即利用傅里叶变换、小波变换等方法提取信号波形频域特征，并与模板频域特征加以比对识别，如文献［7］用上述方法提取特征建立二维时频域空间，并应用子空间投影法进行波形识别，但该方法需要最优选择二维窗函数参数，识别无法做到快速、自动；文献［8］同样利用傅氏变换提取频域特征，通过比对加以识别，但系统无法做到自动对比，而且这些方法在通用性、快速简单高效方面存在不足。

因此本文提出一种方法，从信号时域方面入手，采用离散余弦变换提取波形特征以降低频域特征提取过程的复杂度，同时也能省去时域识别方法中提到的“对齐”操作，结合时域分析中的模板匹配思想与神经网络的方法对信号波形加以识别，即：对采集到的波形提取其相关频域信息特征，根据子空间模式识别理论，并结合BP 神经网络的方法，自动识别测试系统中的信号波形类型。最后通过对比验证实验，取得了良好的效果。

2 波形识别方法

本文所使用的波形识别方法按顺序可简要概述为三个部分：1）波形特征提取过程，该过程提取出模板波形的特征信息，为下一步建立识别网络提供原始数据；2）波形模板建立过程，该过程利用第一步中提取出的特征信息建立识别波形类型的神经网络；3）待测波形分类识别过程，在波形识别网络建立完成后，即可将待检测波形送入该网络中进行波形类型的识别。其识别流程图如图1所示，具体识别过程如图1所示。

图1 神经网络识别方法流程图

2．1 波形特征提取［9～10］

由于实际测试系统中待处理的原始信号是连续的模拟信号，而计算机只能处理离散信号，所以在对原始信号进行分析处理之前首先就要依据采样定律将之变换为离散序列，然后利用离散傅里叶变换对离散序列进行分析处理。然而常用的离散傅氏变换往往会牵涉到复数计算，相对增加了计算量，得到的结果往往也是二维复数序列，不便于测试系统的快速高效测量。Ahmed于1974年提出的离散余弦变换（DCT），作为一种实数域变换，它克服了傅氏变换在复数域运算的缺点，因此在数字信号处理、频谱分析等领域有广泛应用。同时，促使其广泛应用的原因包括：1）它有趋于统计最佳变换KLT 变换的渐进性质，且比DFT 逼近程度更好，2）随着其快速算法的出现，人们发现其运算量比DFT 少，处理速度比DFT 快。离散余弦变换公式定义为

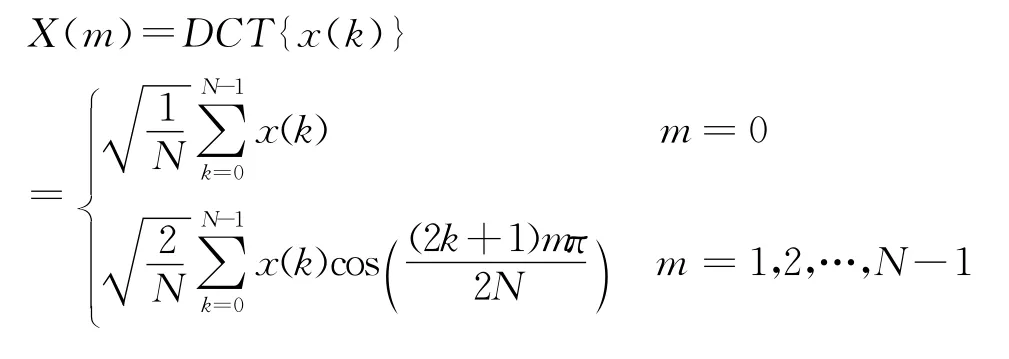
从公式可以看出，DCT 是将信号分解为许多个余弦项之和，所不同的是余弦信号的谐波频率不同。而同DFT 一样，DCT 也是一种正交变换，即满足变换后时域、频域能量保持不变的Parseval定理，对大部分信号来说，能量都集中在DCT 变换后的低频部分，那么可以人为设定一门限值，略去小于此门限的谐波量，得到一个有限长的实数序列。

2．2 波形模板建立［11～12］

在波形特征提取后，接下来进行的工作即是待测波形与模板波形的匹配识别，这其中所使用的理论即是子空间模式识别法。子空间的本质是通过不同的基矢量反映一个数据集。子空间模式识别中的一个线性子空间代表一个模式类别，每个模式类别通过一定规则映射到向量空间，成为其中的一个元素，每一个模式因有反映其特征的特征集而相互区别。即：

假设将一系列如同F＝｛a1，a2，a3，…，an｝的线性无关矢量归一化，得到

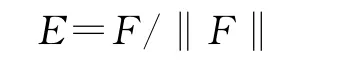
然后将所得的各向量作为矢量空间φ＝｛E1，E2，E3，…，Em｝的归一基，进而形成相应的空间：

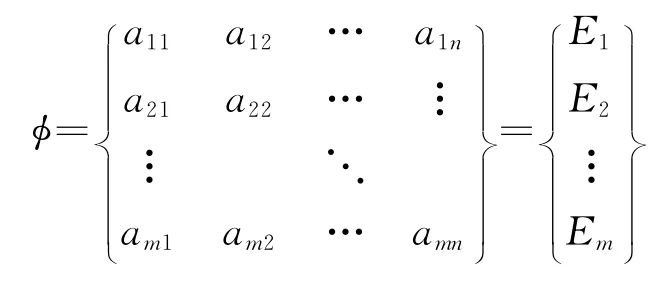
现有一待测矢量K，根据一定的法则将其分别与空间中的各矢量进行匹配度计算求解，而后选出其中匹配值最大的一个基，即认为该待测矢量分类于该空间中的此特征矢量可能性最大。

对于单一特定波形的识别可以直接利用离散余弦变换提取频谱特征，而后求它与各标准信号频谱的匹配度，找出其中对应匹配值最大的信号波形即识别出了该待测波形。但对于同一类不同参数的信号，诸如不同幅度、角频率或相位的正弦波，不同幅度、占空比的方波，亦或是不同幅度、占空比的三角波等等。上述方法具有很大的局限性：一方面若存在这样的空间则识别中计算量太大，另一方面也不可能穷举出所有波形，也就提取不了所有的特征矢量，即不存在这样一个空间。

随着神经网络的出现，关于这方面的问题得到了很好地解决。神经网络是近20多年来十分活跃的学科，通过模拟人脑结构和功能，相对于传统方法，具有一些明显优势，如容错性即能识别有噪声干扰或畸变的输入信息，模块化、高效、自适应的学习能力等等，所以在模式识别领域中具有重要的应用。其中由于神经网络具有记忆联想、优化计算等性质，在分类识别中有着广泛的应用。

于是利用前述的波形特征提取方法提取大量同类波形数据特征送入神经网络训练，使网络能够记忆和预测此类波形的特征，重复此种方法使网络能记忆、预测不同类波形特征，训练得出的每一类波形的特征可看做是子空间模式识别法中所说的子空间的一个特征集，不同的特征集便组成一个子空间。

本文中采用BP 神经网络的方法对波形进行分类识别。神经网络是一种多层前馈神经网络，即信号前向传递，误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。每一层神经元状态只影响下一层神经元状态。如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使预测输出不断逼近期望输出。通过网络训练，使其具有联想记忆和预测能力。其拓扑结构如图2所示，图中X是输入值，Y是输出值，W和U为神经网络权值。

2．3 待测波形分类识别

在完成波形模板建立后，可对待测波形进行分类识别，其过程为：首先，利用离散余弦变换分别提取波形频域特征信息，并根据门限限制设定本文在验证中取每个波形变换后得到的矢量的前18项元素数值作为特征矢量。

在将这些矢量送入神经网络学习训练之前，首先要将其各元素做归一化处理，使之都转化为［0，1］之间的数，避免因数量级差别过大引起较大的网络预测误差，这是神经网络预测前的一种常用处理方法，该方法的函数式表示为

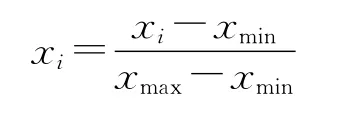
在创建BP神经网络过程中，根据识别波形的种类设置输出层个数和期望输出向量，并根据输入输出层的个数选择最优的隐含层个数（例如本文在实验中最终待识别种类为正弦、余弦和三角波，最终设定BP神经网络结构为18—11—3，期望输出向量设定为正弦波［1 0 0］，方波［0 1 0］，三角波［0 0 1］。

在进行网络训练之前，还需预设训练参数。本文方法所用的参数设置为：最大训练时间为100个时间单位，学习率为0．1，训练目标为误差小于0．00001，经过大量BP神经网络实验分析，选择一组对预测误差和均方误差的影响最小传递函数，即输入层与隐含层之间的传递函数选为S 型函数“logsig”，它能将输入映射到区间［0，1］中，隐含层与输出层之间的传递函数选为纯线性传递函数“purelin”，其他参数保持默认值。在神经网络结构初始化之后，即可进行神经网络的学习训练，用以从大量的数据样本中根据网络预测误差，筛选出最优的权值和阈值。

最后，将待检测波形各自的频域特征向量分别送入已训练好的神经网络进行学习训练，并通过神经网络的分析得出结果实现对各待检测波形的分类识别。

3 波形识别实例与实验结果分析

在实际仿真验证中，本文用BP 神经网络从已有的标准波形数据库中选择正弦波、方波和三角波三种类型的波形各300组送入神经网络进行训练，建立分类识别待测波形时所需的神经网络。为对比本文所用方法的效果，选取前述提到的MCC 法和MCD 法加以对比。

实验中所用的待测波形存在诸如白噪声干扰，频域干扰，信号局部畸变等等不利影响，现列举部分识别对比情况如下：

第一种情况为待测波形是正弦波叠加噪声后三种方法的识别情况，其中方波、三角波占空比都为0．5，且各信号间无时延，各波形识别时幅度已归一化不产生影响。如图3所示。

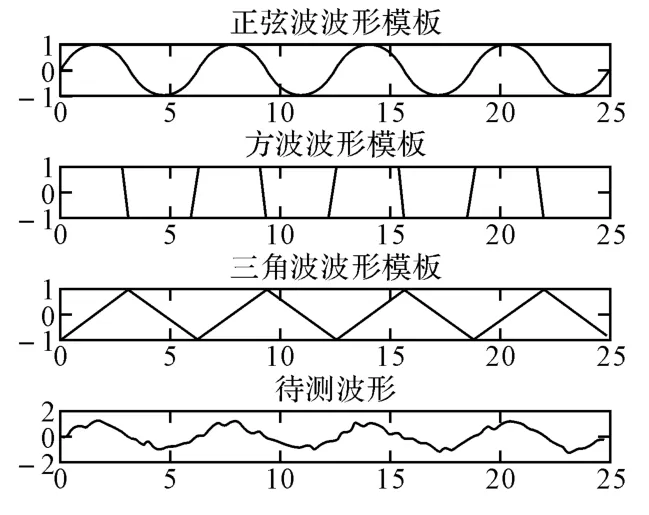
图3 叠加噪声干扰时的待测波形与模板波形

利用MCC法时对正弦波、方波、三角波各自的相似度为0．9979、0．8897、0．9997，判断为三角波；MCD 法时对应相似度为0．9954、0．9963、0．9919，判断为方波；本文方法经网络判断后判定为正弦波。

第二种情况为待测波形是正弦波相对模板时延0．25个周期并发生局部畸变时三种方法的识别情况，其中方波、三角波占空比都为0．5，各波形识别时幅度已归一化不产生影响。如图4所示。

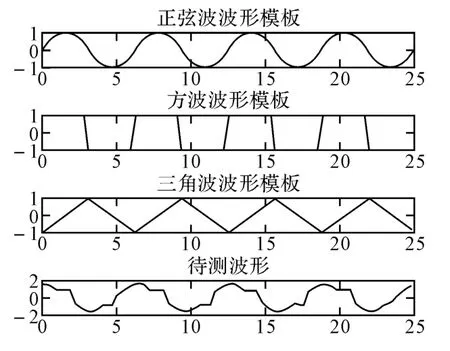
图4 局部放生畸变时的待测波形与模板波形

利用MCC法时对正弦波、方波、三角波各自的相似度为0．9679、0．9719、0．9645，判断为方波；MCD法时对应相似度为0．9985、0．9634、0．9975，判断为正弦波；本文方法经网络判断后判定为正弦波。

第三种情况为待测波形是方波经频域干扰时三种方法的识别情况，其中方波、三角波占空比都为0．5，各波形识别时幅度已归一化不产生影响。如图5所示。

利用MCC法时对正弦波、方波、三角波各自的相似度为0．8721、0．9801、0．7833，判断为方波；MCD法时对应相似度为0．9844、0．9913、0．9890，判断为方波；本文方法经网络判断后判定为方波。

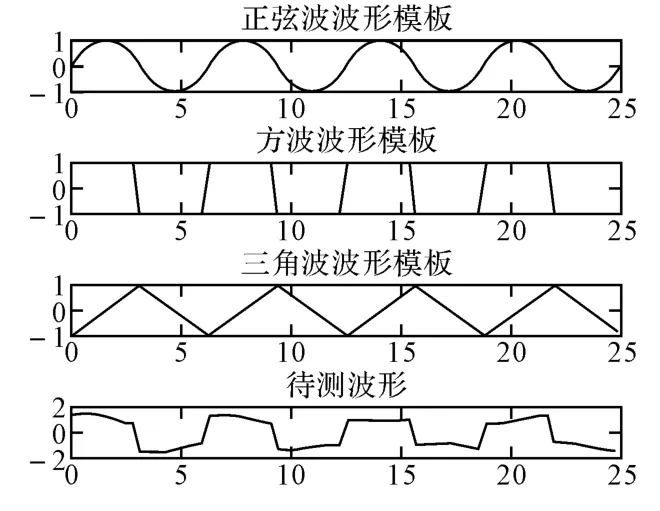
图5 存在频域干扰时的待测波形与模板波形

为对比本文方法与其他方法的整体通用性能好坏，将一定数量（三种波形混合共计300组）的存在上述各种干扰的待测样本分别用上述三种方法进行波形的分类识别，并统计各自的识别正确率，三种方法最终判别误差如表1所示。

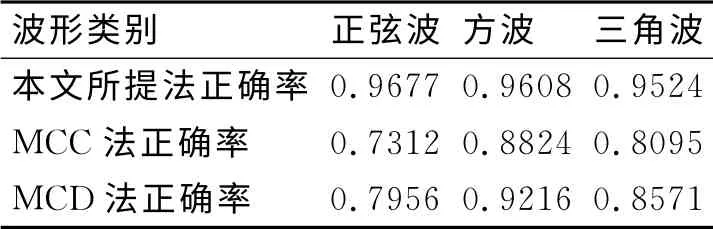
表1 识别正确率结果

通过单一情况对比，可以发现，在信号存在噪声干扰的情况下，MCC、MCD 都存在误判的情况；信号存在局部畸变时MCC 有误判，MCD 识别结果上正弦波、三角波相似值极接近，效果不突出；信号有频域扰动时三种方法都识别正确。进一步通过大量数据对比整体通用性，结合上表结果可以发现，应用空间模式识别结合神经网络的方法对波形进行分类识别在识别效果上明显优于其他两种方法。

4 结语

本文所提方法很好地解决了待测波形与模板波形匹配过程中的相位对齐过程，省去了其他波形识别算法中所常用到的“波形对齐”操作，识别过程简易高效，识别效果良好，可以应用到测试系统对信号波形的分类识别中，具有一定的实际应用性。但同时，本方法在对待测波形的识别上要求信噪比不能过高，在识别极小（少于0．005）占空比的方波与三角波方面也存在不足，导致表中会有误判的情况，可作为以后进一步深入研究改进的方向。

［1］Craelius W，Restivo M，et al．Techniques for processing of cardiac sigals：fiducial formulae for fidelity［J］．High-resolution Electrocadiography．Futura Publishing Co Inc．Mount Kisco NY，1992：21-49．

［2］Lander P，Berbari E J．Princeple and signal processing techniques of the high-resolution electrocardiogram［J］．Prog in Cardiovasc Dis，1992，35：169-188．

［3］Escalona O J，Mitchell R H．Frequency bandwidth limitations in the signal-averaged ECG by the maximum coherence matching technique［J］．Automedica，1991，13：177-186．

［4］Craelius W，Restivo M，et al．Signal processing options for detecting conduction abnormalities in ischemic ven-tricles［J］．Electrocardiology，1987，20（suppl）：119-124．

［5］程小明，林金森，张正国．高分辨心电图中模板匹配算法的改进［J］．中国生物医学工程学报，1999，18（1）：85-96．

［6］练仕榴，郑刚，牟善玲．用于心电波形分析的相似性度量策略［J］．计算机工程，2011，37（9）：263-265．

［7］王俊，张守宏．一种基于子空间匹配投影的暂态信号检测方法［J］．系统工程与电子技术，2000，22（1）：22-24．

［8］姜新华，金玮，范征宇，等．基于数字信号处理的局部放电在线监测系统［J］．计算机自动测量与控制，2000，8（1）：28-30．

［9］刘瑞阳，张端强．基于离散余弦变换的时间序列相似性检索［J］．计算机系统应用，2012，21（9）：195-197．

［10］曾泳泓．基于离散余弦变换快速算法［J］．数值计算与计算机应用，1994（1）：52-58．

［11］王洪，吕幼新，向敬成．一种新的子空间模式识别方法［J］．电子科技大学学报，2004，33（1）：5-8．

［12］E．奥亚．子空间法模式识别［M］．蔡国廉，杨文瑜，译．北京：科学出版社，1987：61-82．