Δ（G）≤2的图的Cordial性

徐丽平，李治

（长江大学信息与数学学院，湖北 荆州434023）

1987年Cahit引出Cor dial图的概念［1］，给定图G的顶点集合V（G）一个0－1标号，记为f，以导出G的边集合E（G）上的标号，记Vi＝Vi（G）＝｛u／u∈V（G），f（u）＝i｝，Ei＝Ei（G）＝｛uv／uv∈E（G），f（uv）＝i｝，i＝0，1。并以vi（G），ei（G）分别表示它们的基数，若图G存在一个标号f，使得则称G是Cor dial图，f是一个Cordial标号；若v0（G）＝v1（G），e0（G）＝e1（G），则称G 是严格Cordial图，f是一个严格Cordial标号。这种标号引起人们的广泛兴趣，已有很多论文如文献［1－7］研究了各种图的Cordial性，但是关于并图的Cordial性的研究仅限于分支十分简单的图，如关于圈的并只限于2个分支Cm∪Cn［2］，或虽是多个分支但各图的阶数必须相同的情况［2］，而对于路与圈的并图的Cordial性尚无人考虑。下面，笔者研究Δ（G）≤2的图的Cordial性，包括了分支为路或圈的各种情况，旨在为今后研究Δ（G）≤3的情况作好准备。

Δ（G）≤2的图可以分为Δ（G）＝0、Δ（G）＝1、Δ（G）＝2这3类。下面，笔者分别讨论这3类图的Cor dial性。

1 Δ（G）＝0的图的Cordial性

Δ（G）＝0表示图G中所有的顶点都是孤立点。若图G有2n个顶点，那么只需对其中n个标0，另外n个标1，则v0（G）＝v1（G）＝n，e0（G）＝e1（G）＝0，即得到图G的一个Cordial标号；若图G有2n＋1个顶点，只需对其中n＋1个顶点标0，另外n个标1，则v0（G）－v1（G）＝1，e0（G）＝e1（G）＝0，即得到图G的一个Cor dial标号。因此，当Δ（G）＝0时，图G是Cor dial图。

2 Δ（G）＝1的图的Cor dial性

定义 符号D（i1，i2，…，ik）表示顶点度组成的集合为｛i1，i2，…，ik｝的一类图。

Δ（G）＝1这样的图可以分为D（1）和D（1，0）。

引理1［4］设f是图G的一个标号。

1）若V0（G）中奇度点的数目为奇数，则e0（G）与e（G）的奇偶性相异；

2）若V0（G）中奇度点的数目为偶数，则e0（G）与e（G）的奇偶性相同。

D（1）是由P2构成的图类，当G∈D（1）且e（G）＝4k＋2时，假设该图G有Cor dial标号，则v0（G）＝4k＋2为偶数，e0（G）＝2k＋1，与引理1矛盾，从而当e（G）＝4k＋2时，G不是Cor dial图；容易验证对于 ∀G∈D（1），当e（G）＝4k、e（G）＝4k＋1、e（G）＝4k＋3时，G是Cor dial图。

D（1，0）是由P2和孤立点构成的图类，容易验证每个D（1，0）图是Cor dial图。

3 Δ（G）＝2的图的Cor dial性

当Δ（G）＝2时，这样的图又可以分为D（2）、D（2，0）、D（2，1）、D（2，1，0）4类。

3.1 D（2）

D（2）是由圈构成的图类，也称二正则图，由文献［4］知，∀G∈D（2）当且仅当时，G是Cordial图。

3.2 D（2，0）

D（2，0）是由圈和孤立点构成的图类，则D（2，0）是偶度图，由文献［4］推论1知，当G∈D（2，0）且e（G）≡2（mod4）时，G不是Cor dial图；易验证对于∀G∈D（2，0），当e（G）≡0（mod4）、e（G）≡1（mod4）、e（G）≡3（mod4）时，G 是Cor dial图。

3.3 D（2，1）

D（2，1）是由圈和路构成的图类，且至少有一个分支为路，但不能每个分支都是P2。

引理2 若图G＊＝G1∪Ck是Cordial图，则G＝G1∪Ck＋4也是Cordial图。

证明 由文献［4］中的引理2可得出结论。

引理3 若图G＝G1∪Pk是Cor dial图，则G＊＝G1∪Pk＋2也是Cor dial图。

显然：

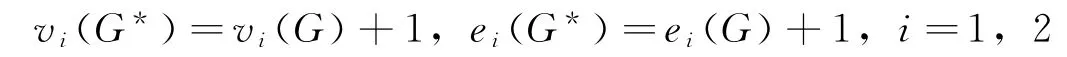
从而：

即g是G＊的Cor dial标号，从而G＊也是Cor dial图。

由引理2、3知，欲证D（2，1）的图G的Cor dial性，可假定G的分支都是C6，C5，C4，C3或P3，P2，并且至少有一个分支是P3或P2以及分支不能全是P2。

引理4 若图G1有标号f1，使得且G2是Cordial图，则G＝G1∪G2是Cor dial图。

证明 设G2有标号f2，使得：

由于G＝G1∪G2，那么：

设：

首先把G2的顶点的0，1标号互换，这不影响G1的标号，且仍有e0（G2）＝e1（G2）＋1，只是v0（G2）＝v1（G2）＋1变成v0（G2）＝v1（G2）－1。于是：

从而G＝G1∪G2是Cordial图。

证明 由于这些图比较简单、具体，寻找满足条件的标号f很容易。仅以（8）和（11）为例给与证明。（8）中3个C3的顶点标为（0，0，1），一个C3的顶点标为（1，1，1），即得到满足条件的标号f；（11）中C6的顶点标为（0，0，1，0，1，1），2个C5的顶点分别标为（0，0，0，1，1），（1，1，1，0，0），则得到满足条件的标号f。

设G＝m1C6∪m2C5∪m3C3∪m4C4∪n1P3∪n2P2。由引理4及引理5的（1）（2）（3）（8）（9）（13）知，只需对情况m4＝n2＝0，m1∈｛0，1｝，｛m2，m3，n1｝⊂｛0，1，2，3｝，但m1，m2，m3，m4不同时为零，n1，n2不同时为零。又由（4）可假设m2，m3至少有一个为零，由（6）（7）可假设m2与n1及m3与n1至少一个为零。

图G经过以上约简后，会出现4种情况：

1）约简后的图为空图。由引理4知，原来的图G是Cor dial图。

2）约简后的图为2P2。因为D（2，1）必有2度点，则在约简的过程中一定删除了2C6或C4或C3∪C5、4C3、4C5、P3，那么可在约简的过程中保留一个删减的分支，易验证2C6∪2P2、C4∪2P2、C3∪C5∪2P2、4C3∪2P2、4C5∪2P2、P3∪2P2都是Cordial图。由引理4知，原来的图G是Cordial图。

3）约简后的图为C6或2C3或2C5。因为D（2，1）必有1度点，则在约简的过程中一定删除了含有1度点的图。当约简后的图是C6时，必删除了4P2或P3或C5∪P2或C3∪P2，可以验证4P2∪C6、P3∪C6、C5∪P2∪C6、C3∪P2∪C6都是Cor dial图；当约简后的图为2C3时，必删除了4P2或P3或C3∪P2，易验证4P2∪2C3、P3∪2C3、C3∪P2∪2C3都是Cordial图；当约简后的图为2C5时，必删除了4P2或P3或C5∪P2，易验证4P2∪2C5、P3∪2C5、C5∪P2∪2C5都是Cor dial图；由引理4知，原来的图G是Cordial图。

4）约简后的图为C6∪P2或3C5或3C3或C5∪P3或C3∪P3，由于这些图不在定理5中，所以在约简过程中不能被删掉，但容易验证这些图都是Cordial图。由引理4知，原来的图G是Cor dial图。

由以上讨论可以得到：每个D（2，1）图都是Cor dial图。

3.4 D（2，1，0）

D（2，1，0）是由D（2，1）中的图和孤立点构成的图类。由每个D（2，1）图都是Cor dial图及Cordial图添加孤立点后仍为Cor dial图可得，每个D（2，1，0）图也是Cor dial图。

从以上讨论可知，除了D（1）、D（2）和D（2，0）中边数为4k＋2的图外，其余的Δ（G）≤2的图都是Cordial图。

［1］Cahit R.Cordial graphs：A weaker version of gracef ul and har monious graphs ［J］.Ars Co mbinatoric，1987，23：201－208.

［2］Joseph A.Gallian，A Dyna mic Survey of Graph Labeling ［J］.The Electr onic Jour nal of co mbinatorics，2005，5：41－42.

［3］Cahit I.On Cor dial and 3－equit bale labeling of graphs ［J］.Utilitas Mat h，1990，37：189－198.

［4］徐丽平，刘峙山，倪臣敏 .二正则图的Cordial性 ［J］.延边大学学报（自然科学版），2008，34（1）：21－22.

［5］陈丽娜，刘峙山 .一类图的Cordial性 ［J］.数学研究，2007，40（4）：446－451.

［6］张升，堵根民 .圈轮的Cordial性 ［J］.内蒙古师大学报自然科学（汉文）版，1999，28（4）：7－11.

［7］堵根民 .轮族的Cordial性问题 ［J］.内蒙古师大学报自然科学（汉文）版，2008，37（2）：180－184.