随机扰动下的金融混沌系统动力学演化分析

徐玉华，谢承蓉，李军

（郧阳师范高等专科学校数学与财经系，湖北 十堰442000）

目前，人们不仅关心通过数据的研究验证混沌现象，也普遍关注随机现象对金融复杂系统的动力学行为是如何影响的［1－2］。通过分析随机现象对金融复杂系统动力学的影响，可以了解受随机扰动（内部扰动和外部扰动）下的金融复杂系统的动力学特征，这样有利于分析如何保持金融复杂系统的稳定性，避免金融风险。由混沌理论可以知道，对混沌系统的微小冲击可以显著地改变系统的行为，由于随机金融模型和非随机金融模型的数学结构是不同的，随机扰动对系统的动力学特征会产生一定的影响［3－6］。

黄登仕等［7］建立的金融模型给出了某些长期行为具有无规则性及其对状态初值的参数变化极端的敏感性，该模型简化仅含3个最主要参数的简单模型：

式中，x表示利率；y表示投资需求；z表示价格指数；a为储蓄量；b为投资成本；c为商品需求弹性。下面，笔者将分析系统（1）在外部和内部扰动情况下的动力演化性质。

1 混沌动力系统外部扰动情形

考虑如下随机外部扰动下的金融系统：

式中，a＝0.9；b＝0.2；c＝1.2；σ（t）是有界噪声扰动函数；wi（t），i＝1、2、3是一个1维布朗运动。

为了分析微小扰动对混沌系统动力学的影响，假设噪声扰动函数是有界的，且很小，当扰动较大时，对金融系统可能产生颠覆性的影响，系统的动力学就会完全改变。

设σ（t）˙w1＝0，σ（t）˙w2＝d sin wt，则系统（1）变为：

1.1 耗散性和吸引子的存在性

对于金融系统（3），有下列表达式：

因此随机有界扰动的金融混沌模型（3）是耗散的，其指数收敛形式如下：

即体积元V0在时刻t时收缩为体积元V0eft＝V0e－2.3t。这表明当t→∞，系统轨线的每个体积元均以指数率z收缩到0。因此运动轨迹固定在一个吸引子上。

1.2 分数维与李雅普洛夫指数

李雅普洛夫指数是刻画系统邻近轨道平均分离快慢的平均量，若系统的最大的李雅普洛夫指数大于零，则通常认为系统是混沌系统。对于系统（3），当d＝0.1，w＝0.1时，计算得到系统的李雅普洛夫指数为L1＝0.3573，L2＝－0.0005，L3＝－0.4532，李雅普洛夫分数维是：

1.3 平衡点的稳定性

令：

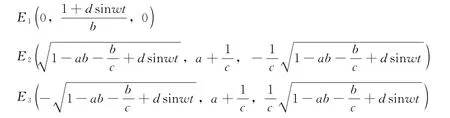
经计算，系统的特征方程都为：

则其中之一特征根为λ1＝－b＜0，另外2个特征根由下列方程决定：

即：

从上面讨论可知，扰动d sin wt显然会影响系统的稳定性。

另外，对于平衡点E1，x＝0，y＝z＝0， 将d sin wt＝σ（t）˙w2代入E1， 则y＝即σ（t）d w2＝（yb－1）d t，两边取期望Eσ（t）d w2＝Ε（yb－1）d t，如要得到理性预期均衡点，可假设金融系统随机扰动满足E d w2＝0即可，也就是Eσ（t）d w2＝Ε（yb－1）d t＝0，即对于平衡点E2，3也可作类似讨论。

1.4 边界、重心、谱图，庞开莱图和分岔图

当d＝0.1，w＝0.1时，经仿真可得到动力系统扰动后的边界为：

而系统扰动前的边界为：

显然，扰动后的系统边界扩大。同时边界也表明混沌系统是有界的。另外，也可得到吸引子的重心（见图1），它表明吸引子轨迹运动围绕重心达到平衡。图2显示了金融系统的连续宽带特征。图3为新系统在x＝1上庞开莱映像，映像中的吸引子的叶片被折叠，这就导致了金融混沌系统复杂的动力学行为。另外，对于参数变化，金融系统的分岔图（见图4）展示了金融系统有复杂的分岔特性。

图1 吸引子的重心

2 混沌动力系统内部扰动情形

考虑如下随机有界扰动下的金融系统：

图2 金融混沌系统的功率谱

图3 金融混沌系统的庞开莱图（x＝1）

设σ（t）˙w1＝0，σ（t）˙w2＝0，σ（t）˙w3＝d sgn z，系统（5）变为：

下面仅讨论扰动项对动力系统形成机制的影响。从仿真图5～图10可看出，扰动项对混沌系统形成机制是有影响的，扰动后的混沌系统是由2个涡卷共同形成的。

混沌动力系统内部扰动情形的其他性质类似于外部扰动的分析，这里省略。

图4 金融混沌系统的分岔图（0≤c≤2）

图5 当d＝－0.9时系统的相图

图6 当d＝－0.7时系统的相图

图7 d＝－0.3时系统的相图

图8 d＝0.3时系统的相图

图9 d＝0.7时系统的相图

图10 d＝0.9时系统的相图

3 结语

通过分析在扰动的情况下金融混沌系统的动力学演化性质可知，在扰动不太大的情况下，系统仍然能保持混沌特征；但是对金融混沌系统的微小外部扰动或者微小内部扰动都可以显著地改变金融混沌系统的动力学行为，如平衡点的稳定性、吸引子边界的范围、李雅普诺夫指数的大小、分数维的大小、吸引域的范围，甚至是系统的形成机制都有所改变。

［1］徐寅峰 .经济模型及经济混沌 ［J］.西安交通大学学报，1994，125（2）：92－95.

［2］李红权，罗思哲 .金融市场的复杂性与金融风险调控 ［J］.金融理论与实践，2009，385（5）：8－11.

［3］辛宝贵，陈通，刘艳芹，等 .一类分数阶混沌金融系统的复杂性演化研究 ［J］.物理学报，2011，4（048901）：（1－6）.

［4］何孝星，赵华 .关于混沌理论在金融经济学与宏观经济中的应用研究述评 ［J］.金融研究，2006，313（7）：166－173.

［5］马军海，盛昭瀚，陈春旺，等 .经济时序动力系统的分形及混沌特性研究 ［J］.系统工程学报，2000，15（1）：13－18.

［6］姚洪兴，石桃丽 .一类金融市场模型的混沌控制 ［J］.微计算机信息，2007，23（9）：50－53.

［7］黃登仕，李后强 .非线性经济学的理论与方法 ［M］.成都：四川大学出版社，1993.