运用“一题多解” 提高复习效率——数学思想与方法的融合

◆陈兴国

(杭州市公益中学)

教育家苏霍姆林斯基说过:“真正的学校是一个积极思考的王国。”数学教学中，高效的复习课堂特别重视学生拓展性思维能力的培养，这已是所有教师的共识。要培养学生进行灵活思考，多角度看问题，多方位处理问题进行拓展性思维，其主要方法就是拓宽思路，一题多解，善于联想，发散思维。特别针对中学几何证明和求解的多样性，要求学生在做题时能善于观察、思考，从不同角度分析问题，力求灵活驾驭所学知识。一个数学问题，如果我们只有一个解法，无论是自己想出来的还是查答案看到的，都或多或少会存在认识上的局限性。只有在得出两个或多个解法后，学生才能对问题的实质有真正的了解，通过解题而加强知识之间的联系以形成知识网络，从而培养解题能力的目的才有可能得以实现。我们仅以下面这道题目来说明这个道理。

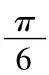
本题的第(1)问相对比较简单，这里就不展开介绍，给出一种参考答案如下:

第(2)问解法一:

分析:由已知条件直径AB=2，再利用角平分线性质过点E作EF⊥AB于点F，根据勾股定理、三角形相似可求出相应线段长度及关系。

解如图2，过点E作EF⊥AB于点F

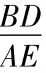
解法二:

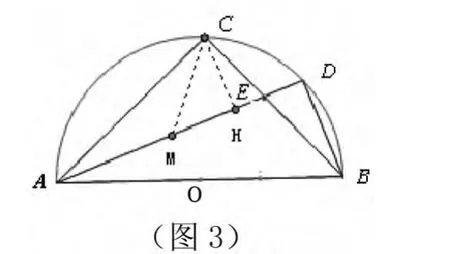
分析:如图3，可以找AE中点M，根据直角三角形斜边上中线等于斜边的一半得AE=2CM，然后作CH⊥AE根据相似求得，再由CM、CE之间的关系求出答案。

解:如图3，找AE的中点M且连接AM，作CH⊥AE交AE于点H，

∵AB是直径，∴AC⊥BC，∴Rt△ACE中AE=2CM ，AM=CM，

又∵CH⊥AE，AD⊥BD∴CH∥BD ∴△CHE ～△BDE，

又∵ Rt△MHC 中∠CMH=22.5 o×2=45 o

解法二巧妙地利用相似找出DB与CH的关系，由CH与CM的关系发现CM=DB，再通过直角三角形斜边上的中线的性质得出AE是CM的2倍，从而得到的比值。这里利用线段CE、CM为桥梁，培养了学生一种“转化思想”。

解法三:

分析:如图4，连接OD交CB于点P，根据OD∥AC可以推得

解:连接OD交CB于点P，∴OD∥AC，

∴∠DPB=∠ACB=90° 又∵∠DBP=∠CAE ∴△CAE～△BDP

解法四:

分析:我们可以先把△ACE独立出来，在Rt△ACE中求出tan22.5°的值，然后根据三角函数值直接计算出相应线段的长度，这种先求出基本图形的函数值再求解的方法在解题中应用比较广泛，值得我们所关注。

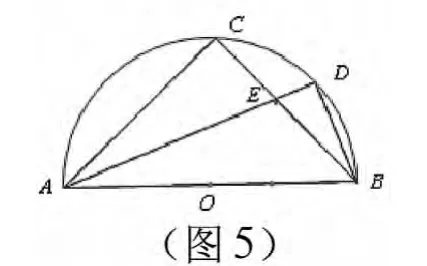
解:如图5，在Rt△ACB中因为AE平分∠CAB，

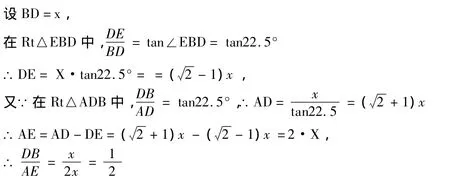
解法四把复杂图形简单化。根据这个图形里面都有22.5°的Rt△，我们先把这个22.5°的Rt△从中抽象出来，然后由这个基本图形的模型分析出他们对应的数量关系，再把这些数量关系带回到原有图形中求出的值，培养了学生一种“建模思想”。

由此例可见，在平时的数学教学中，教师不但要教会学生常规解题的方法，还应向学生提出“一题多解”的问题。这道例题第二小问的六种解法或利用了三角形角平分线的性质、三角形中线的性质、三角形相似的性质、角平分线的性质等求解，或利用了添加不同的辅助线、利用不同的已知条件求解。在这种多种几何图形组合的问题中，往往蕴含着多种几何性质，由此必然蕴含着多种解题思路。

通过对一道题探究多种解法的训练，不仅能够激发学生的学习热情，还提高了学生的思维发散能力，加深了对知识深层次的理解，同时也给学生提供了合作交流与竞争的平台。这样的课堂是高效的课堂，是一种精神与思想的陶冶与洗礼的课堂，对师生均是一种享受。这样的课堂不仅巩固了学生平时所学的基础知识，也对这些知识进行了灵活的综合运用，同时又培养了学生的独创思维，拓宽了解题思路，提高了数学能力。另外，一题多解对促进分层教学也是一种有益的尝试，班级授课通常采用的单一解法有时不能满足学生个性化的需求，一题多解正好能够弥补这方面的不足。

总之，“一题多解”指导思想的根源在于引导学生多反思题境，多总结方法并对所涉及的知识进行剖析、归纳、总结，就能在头脑里形成一个比较完整的知识体系，从而提高运用知识、驾驭知识的能力从而达到提高课堂复习的效率。“学而不思则罔”，只有通过学生尽可能多的反思自己的解题，才能促进学生提高解决实际问题的能力。

［1］周红曼.一题多解，提高复习的效率［J］.中学生数理化?教与学，2011，(4).

［2］王育财.拓宽思路一题多解［J］.数学教学与研究，2012，(5).

［3］袁建华.注重一题多解构建知识网络［J］.中学教学参考，2009，(12).