简单多边形裁剪算法

宋树华，濮国梁，罗 旭，陈 东，陈润强

（1.北京大学 遥感与地理信息系统研究所，北京100871；2.中国资源卫星应用中心，北京100094；3.中煤科技集团公司，北京100013；4.北京应用气象研究所，北京100029）

0 引 言

在多边形裁剪算法中，根据裁剪处理的对象不同，裁剪可分为线段裁剪和多边形裁剪。多边形裁剪较线段裁剪具有更高的使用频率，且多边形越复杂，多边形裁剪算法的难度也越大。经典的多边形裁剪算法，如Sutherland－Hodgeman［1］、 梁－Barsky［2］、 Foley［3］、 Maillot［4］、 Andereev［5］等算法要求裁剪多边形是矩形，罗畏［6］提出的算法则要求裁剪多边形是圆形，而一般多边形裁剪更加实用。Weiler算法［7］、Vatti算法［8］以及 greiner－Hormann算法［9］、刘永奎［10］和彭杰［11］提出的多边形裁剪算法可对处理一般多边形。同时，赵红波［12］和周清平［13］对等值线图的任意多边形窗口裁剪进行研究，陈占龙［14］采用基于要素模型实现多边形裁剪，刘雪娜［15］、王结臣［16］对复杂多边形裁剪进行了探讨。其中，Weiler算法采用树形数据结构，Vatti和greiner－Hormann算法采用双线性链表数据结构，刘永奎、周清平、陈占龙和刘雪娜等的裁剪算法采用单线性链表，彭杰、赵红波和王结臣等的裁剪算法则采用单链表、单指针的数据结构。虽然后两种在复杂性上优于前几种算法，但必须判断多边形顶点的顺时针和逆时针性，增加了多边形裁剪算法的难度。

针对这些问题，本文提出了一个新的多边形裁剪算法，裁剪多边形和被裁剪多边形都可以是一般多边形，且不需要规定多边形输入方向。本算法采用矢量数组结构，只需遍历裁剪多边形和被裁剪多边形顶点即完成多边形的裁剪，具有算法简单、运行效率高的特点。

1 基本概念与定义

为了便于下文对算法的描述，本节将介绍多边形裁剪中涉及的一些概念。

1.1 多边形、顶点及边

由平面上闭合多线段S：｛E0，E1，…，En－1｝（n≥3）称为多边形，其中连接相邻顶点的线段n－1）称为S的边，Pi为顶点。Ei－1，Ei称作Pi的邻边，并规定i的增序方向为S的正方向，否则为反方向。若多边形中不相邻的边不相交，则称该多边形为简单多边形。

1.2 交点、前驱与后继

对于S，若沿着S正方向，则Pi为I在S中的前驱（predecessor），Pi＋1为I在S中的后继 （successor）；若沿着S反方向，则Pi＋1为I在S中的前驱，Pi为I在S中的后继。同理，对于C，若沿着C正方向，则Pj为I在C中的前驱，Pj＋1为I在S中的后继；若沿着C反方向，则Pj＋1为I在S中的前驱，Pj为I在S中的后继。若Ei与Ej交点I为Pj，则在C中，I的前驱和后继均为Pj，如图1（a）中的I8点。

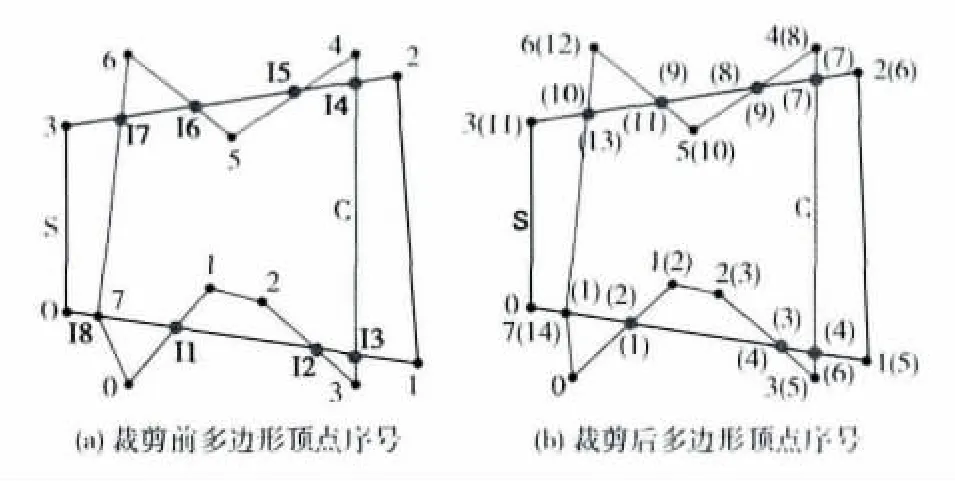
图1 裁剪多边形S和被裁剪多边形C

2 算法的数据结构

多边形裁剪算法的核心是数据结构，它决定了算法的复杂度和计算效率。目前，多边形裁剪常用数据结构为线性链表结构、双向链表结构和树形结构。在算法的复杂性上，线性链表最简单，树形结构最复杂。同时，线性链表比双向链表少一个指针域而节省了存储空间，但指针依然占用空间。因此，兼顾数据结构简单和节省存储空间的目的，本文提出了基于矢量数组vector的数据结构。多边形矢量数组的每个元素表示多边形顶点，且按顶点输入的顺序存储。顶点或交点的数据结构如下：

Vertex＝ ｛double x，y；bool IsInPolygon；｝

交点的前驱后继数据结构如下：

CrossPointIndex｛

int nPredecessorIndex＝0；／／前驱序号

int nSuccessorIndex＝0；／／后继序号

｝

线段的数据结构如下：

Segment｛

int nStartIndex＝0；／／顶点1序号

int nEndIndex＝0；／／顶点1序号

int＊pIndexes；

int nIndexCount；

｝

Vertex用来存储多边形的顶点或交点，x，y表示顶点的坐标，IsInPolygon为true表示该点在多边形内部或在多边形的边上，否则，表示该点在多边形外部。CrossPointIndex用于记录交点在多边形中的前驱与后继的序号信息，以及记录同一交点在两个多边形中顶点序号。即若P为多边形S与多边形C的交点，为了表示P在S和C中为同一点，则可用CrossPointIndex记录用nPredecessorIndex记录P在S中的序号、用nSuccessorIndex记录P在C中序号。Segment表示多边形在另一个多边形内 （外）的线段，nStartIndex为Segment起始顶点的序号，nEndIndex为Segment终止顶点的序号，pIndexes为起始顶点与终止顶点之间的顶点序号集合，nIndexCount为pIndexes中元素个数。

3 算法设计

多边形裁剪算法分为3个阶段。第1个阶段，采用射线法［17，18］计算并判断S （或C）在C （或S）内，并修改S（或C）顶点Vertex的IsInPolygon的值。第2个阶段，按正方向遍历S与C，计算S与C的交点集，交点的前驱后继信息、交点在S和C中对应关系，以及相交多边形弧段集。此阶段是本算法的核心部分。第3个阶段，对弧段集进行合并，生成并输出结果多边形。

第1个阶段文献 ［17，18］讨论的很充分，这里就不再赘述了。下面从第2个阶段开始介绍，以图1为例，具体步骤如下。

步骤1 按正方向遍历S与C并计算交点集Vector＜Vertex＞CrossPointSet，同时生成交点在S和C中前驱、后继信息Vector＜CrossPointIndex＞ CrossPointIndexSetS和Vector＜CrossPointIndex＞CrossPointIndexSetC。其中，CrossPointSet中元素IsInPolygon的值为true。若Cross－PointSet元素为多边形的顶点，如图1（a）中I8与C中序号为7的点为同一点，则CrossPointIndexSetC中对应的元素nPredecessorIndex与nSuccessorIndex的值相等，均C顶点的序号7。表1为交点在在S和C中前驱与后继信息统计表。

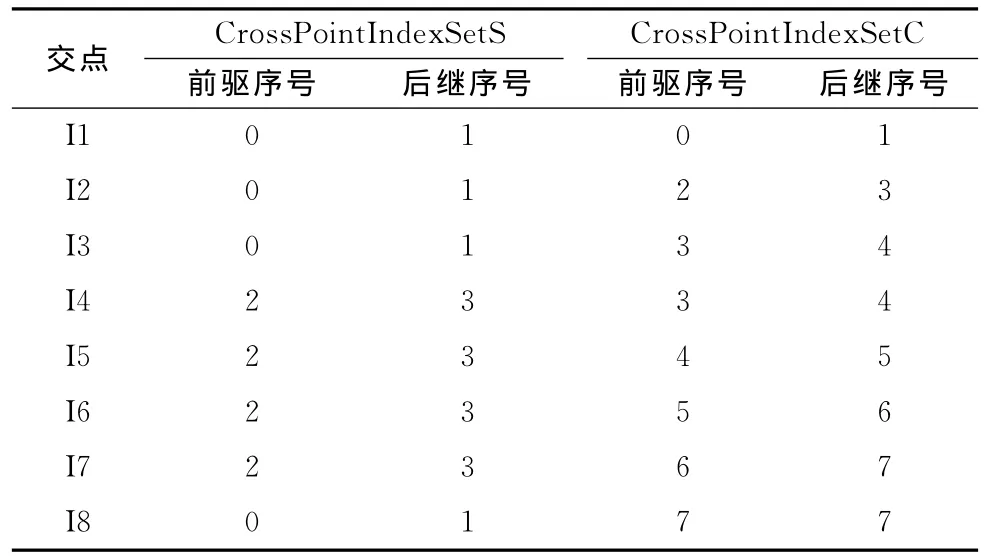
表1 交点在S和C中前驱与后继信息

步骤2 判断CrossPointIndexSetS或CrossPointIndex－SetC中首尾元素的nPredecessorIndex与nSuccessorIndex值是否相等。若相等，则将尾部元素放置到首部位置。重复判断操作，直到首尾元素值不相等为止。表2为表1调整后的结果。

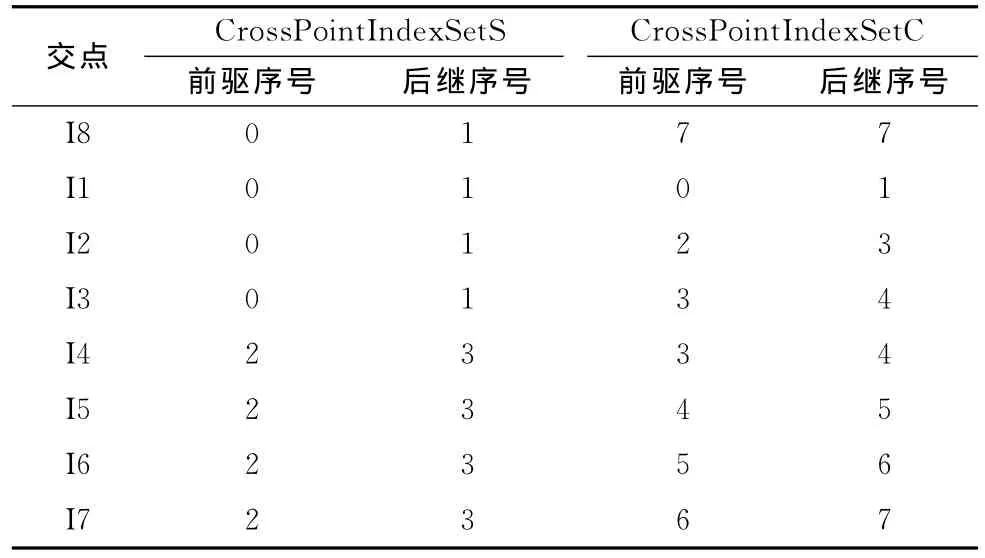
表2 交点集合元素顺序调整后的结果

步骤3 按倒序将CrossPointIndexSetS和CrossPoint－IndexSetC中的元素插入到S和C中，计算原多边形顶点的序号信息，并建立交点在两个多边形中顶点序号对应关系集合。

假设插入交点后的S和C成为S’和C’。插入同时，建立交点在S’和C’中顶点序号对应集合Vector＜Cross－PointIndex＞CorrespondingCrossPointIndexSet，并用nPredecessorIndex记录S’中顶点序号、nSuccessorIndex记录C’中顶点序号。其中，以CrossPointIndexSetS和Cross－PointIndexSetC中前驱序号为0的元素开始，交点序号在前驱序号的基础上顺序递增。根据交点的前驱后继集合信息，S和C顶点在S’和C’中的序号具有如下变化规律：

式中：nPredecessorIndex ［i］、nSuccessorIndex ［i］——S、C序号为i的顶点在S’和C’中的序号，ni——S和C中序号为i与i＋1之间的交点个数。表3是将图1（b）中的交点插入到S和C后顶点序号变化统计表。其中，图1（b）中括号前的数字表示交点插入前顶点序号，括号中的数字表示交点插入后的顶点序号。

表3 多边形顶点序号变化

步骤4 释放CrossPointIndexSetS和CrossPointIndex－SetC空间，修改交点对应集合CorrespondingCrossPointIndexSet的元素值，见表4。

表4 交点对应集合元素值

步骤5 按正方向分别连接S’和C’中Vertex的IsInPolygon为true且相邻的顶点，生成线段集Vector＜Segment＞SegmentSetS和 Vector＜Segment＞ Segment－SetC，见表5。

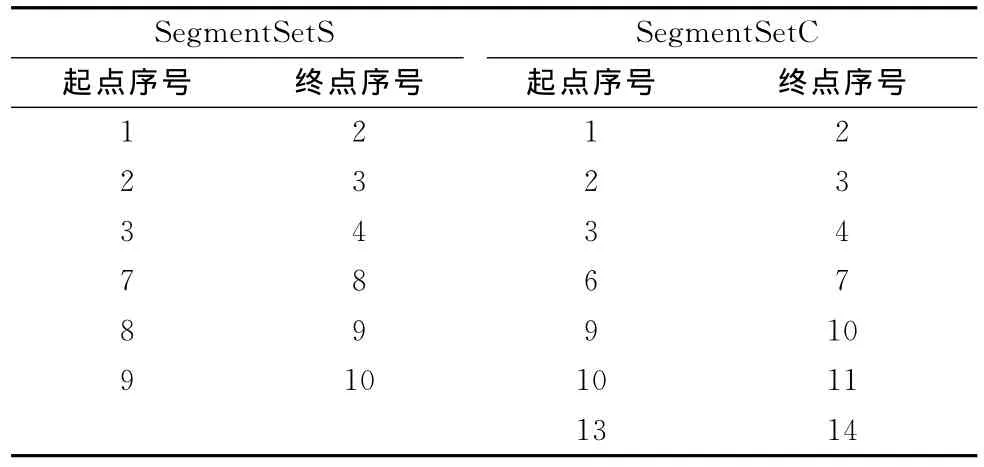
表5 多边形线段集元素的顶点序号表

步骤6 遍历SegmentSetS元素并取第i号元素的中点Pi，采用射线法判断Pi是否在C中，若不在C中，则删除SegmentSetS中第i号元素。同理，删除SegmentSetC中元素的中点不在S’中的项。表6为SegmentSetS和Segment－SetC按照步骤6操作后的结果。

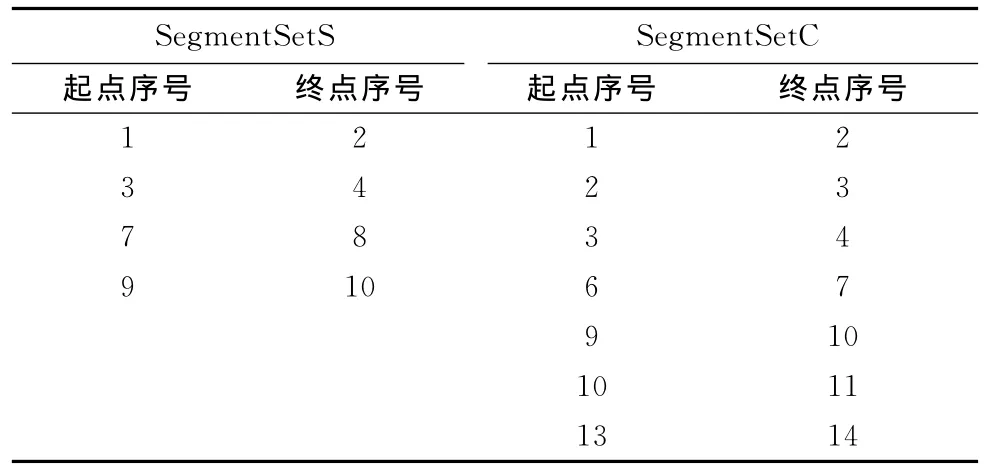
表6 线段集合删除在多边形外元素后的结果

步骤7 分别合并SegmentSetS和SegmentSetC中为相邻边的元素。表7是表6线段合并后的结果。

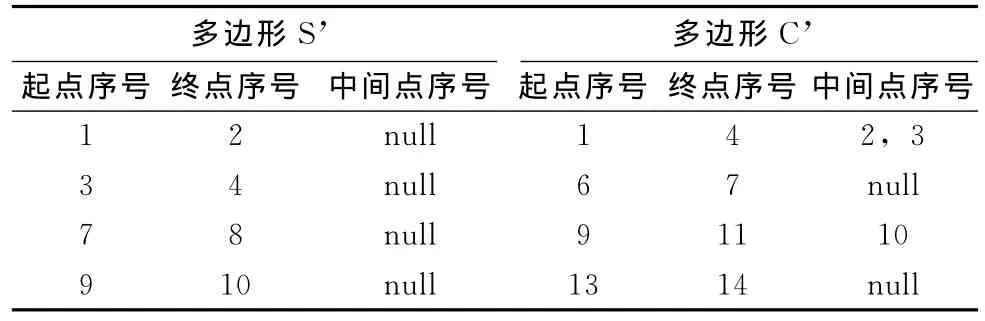
表7 S’和C’的线段合并后的集合

步骤8 遍历SegmentSetS和SegmentSetC，利用CorrespondingCrossPointIndexSet交点在S’和C’的对应关系，将S’和C’互为相邻边或相交的线段连接起来。若SegmentSetS中某元素和SegmentSetC中某元素的值相等或交叉相等，则表示为闭合多边形。线段连接算法如下：

int i＝j＝0；

while（i＜SegmentSetS.Size（））

｛

Segment seg1＝ SegmentSetS［i＋＋］；

int nStart＝seg1.nStartIndex；

int nEnd＝seg1.nEndIndex；

for（j＝0；j＜CorrespondingCrossPointIndexSet.Size（）；j＋＋）

｛

遍历CorrespondingCrossPointIndexSet，得到与S’的nStart、nEnd序号相等顶点的C’序号，用nStart和nEnd记录与S’顶点相应的C’顶点序号。此处，可以删除满足条件的CorrespondingCross PointIndexSet，减少下次循环的次数。

｝

for（j＝0；j＜ Polygon2segments.Count；j＋＋）

｛

Segments seg2＝SegmentSetC［j］；

Segments seg3＝SegmentSetC［j＋1］；

if （（nStart＝ ＝ seg2.nStartIndex ＆ nEnd＝ ＝seg2.nEndIndex））

｛

若线段seg1的起始节点与seg2的起始节点、seg1的终止节点与seg2的终止节点相等，表示线段seg1与seg2组成为一个相交多边形，那么只需将seg2中的点倒序加入到seg1点的后面即可，即点的顺序为：seg1起始点－seg1中间点 （顺序）－seg1终止点－seg2中间点 （倒序）。其中，括号中的顺序是指按Segment中pIndexes元素序号从小到大的先后顺序插入，括号中的倒序则是按pIndexes元素序号从大到小的顺序插入。后面的意义相同。

｝

else if （（nStart＝ ＝ seg2.nEndIndex ＆ nEnd ＝＝seg2.nStartIndex））

｛

若线段seg1的起始节点与seg2的终止节点、seg1的终止节点与seg2的起始节点相等，表示线段seg1与seg2组成为一个相交多边形，那么只需将seg2中的点顺序加入到seg1点的后面即可，即点的顺序为：seg1起始点－seg1中间点 （顺序）－seg1终止点－seg2中间点 （顺序）。

｝

else if （（nStart＝ ＝ seg2.nEndIndex ＆ nEnd ＝＝seg3.nStartIndex））

｛

若线段seg1的起始节点与seg2的终止节点、seg1的终止节点与seg3的起始节点相等，表示线段seg2－seg1－seg3为相交多边形的一部分，那么只需把线段seg1和seg3顶点和中间点追加到线段seg2后面即可，点的操作顺序为：seg1起始点 （或seg2终止点）－seg1中间点 （顺序）－seg1终止点 （或seg3起始点）－seg3中间点 （顺序）。同时，将seg3从SegmentSetC中删除。

｝

else if （（nStart＝＝ seg2.nStartIndex ＆ nEnd ＝＝seg3.nEndIndex））

｛

若线段seg1的起始节点与seg2的起始节点、seg1的终止节点与seg3的终止节点相等，表示线段seg3－seg1－seg2为相交多边形的一部分，那么只需把线段seg1和seg2顶点和中间点追加到线段seg3后面即可，点的操作顺序为：seg1终止点 （或seg3终止点）－seg1中间点 （倒序）－seg1起始点 （或seg2起始点）－seg2中间点 （顺序）。同时，将seg2从SegmentSetC中删除。

｝

｝

算法结束，即可输出结果多边形。根据上述算法，结果多边形形成的过程见表8。

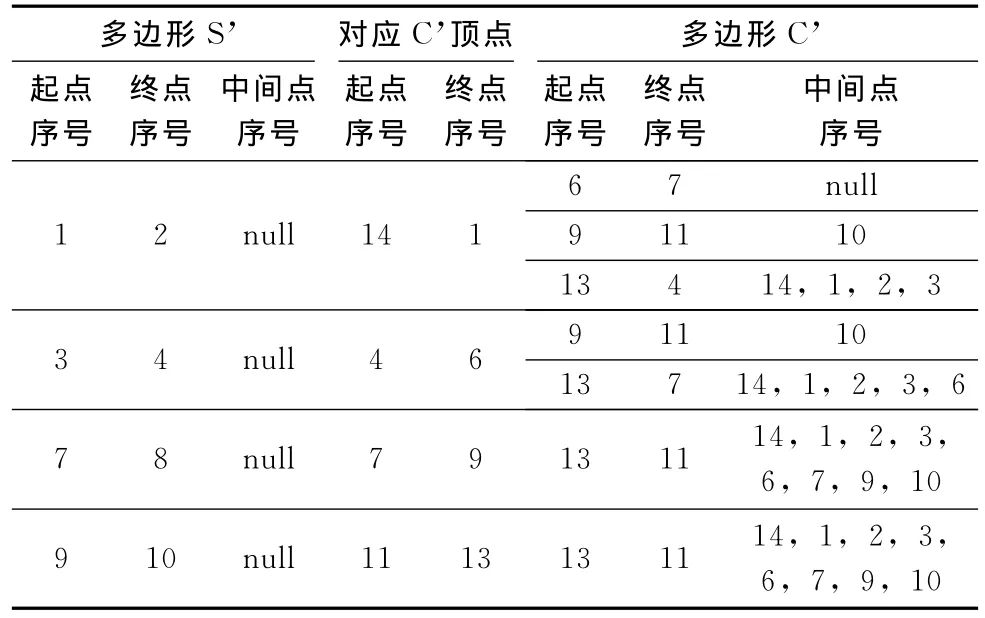
表8 结果多边形形成的过程

该算法不仅可以求多边形的 “交” （多变形的裁剪），而且也可以求多边形的 “并”和 “差”。例如，在求多边形的 “并”时，只需将交点与被裁减多边形和裁剪多边形的外点 （IsInPolygon为false）连接，即为结果多边形；而对于多边形的 “差”，只需将交点与被裁减多边形外点 （IsIn－Polygon为false）连接，即可结果多边形。

4 算法分析

下面从空间复杂性和时间复杂性上对算法进行分析。

首先对空间复杂性分析。假设S和C的顶点数分别为n和m（m＞n），交点数为k。根据文献 ［10］所述，文献［10］中算法需要5（n＋m）＋6k个存储单元，Vatti算法和Greiner－Hormann算法占9（n＋m＋2k）个存储单元。

对于本文的算法，每个顶点和交点只占用3个存储单元，交点前驱后继数据结构占2个存储单元，弧段占用4个存储单元。由于交点前驱后继数据结构在对每个多边形都记录一次，因此一个交点的前驱后继占用4个存储单元；在申请弧段结构时，前驱后继结构是不同时存在的，那么在整个算法实现过程中，交点前驱后继信息和弧段信息始终为4个存储单元。因此，本算法总的存储单位为

因此，本算法中的顶点占用的空间比文献 ［10］的顶点所占用的空间将尽少一半，交点占用存储空间比文献［10］算法多k个单元。而相对于 Vatti算法和Greiner－Hormann算法，则节约6（n＋m）＋11k个存储单元，几乎少用了2／3的存储空间。

其次，时间复杂度分析。第1阶段生成交点以及点是否在多边形内，遍历多边形1次，其时间复杂度为o（m×n）；第2阶段步骤1，判断多边形交点对应关系，遍历交点前驱后继集1次，时间复杂度为o（k×k）；步骤6判断线段集合元素的有效性，遍历线段集合和多边形1遍，其中线段集合元素最多不超过k、多边形边数不超过 （m＋k），因此最坏情况下的时间复杂度为o（（m＋k）×k）；步骤7和步骤8，分别是线段合并和线段连接，遍历线段集合1遍，由于线段集合、顶点对应集合的元素的个数均不超过k，所以最坏情况的时间复杂度为o（k×k）。因此，本算法的时间复杂度为o（（m＋k）×k）。

5 结束语

本文综合考虑现有多边形裁剪算法的优缺点，提出了一种基于多边形顶点遍历的简单多边形裁剪算法。本算法通过采用矢量数组结构、遍历多边形顶点并记录裁剪多边形和被裁减多边形交点及其前驱、后继信息，而无需考虑输入多边形的方向、形状等，即可很好地处理多边形边重合、边顶点相交等特殊的情况，实现多边形裁剪。结果表明，本算法具有算法简单、易于实现、运行效率高的特点。

［1］Sutherland I E，Hodgeman G W.Reentrant polygon clipping［J］.Communications of the ACM，1974，17 （1）：32－42.

［2］Liang Y，Barsky B A.An analysis and algorithm for polygon clipping ［J］.Communications of the ACM，1983，26 （11）：868－877.

［3］Foley J D，Dam A，Feiner S K，et al.Computer graphics，principles and practice［M］.MA：Addison－Wesley，1990.

［4］Maillot P G.A new，fast method for 2Dpolygon clipping：Analysis and software implementation ［J］.ACM Transactions on Graphics，1992，11 （3）：276－290.

［5］Andereev R D.Algorithm for clipping arbitrary polygons ［J］.Computer Graphics Forum，1989，8 （2）：183－191.

［6］LUO Wei，ZOU Zhengrong.An algorithm of polygon clipping against a circular window ［J］.Science of Surveying and Mapping，2011，36 （3）：234－235 （in Chinese）.［罗畏，邹峥嵘.一种基于圆形窗口的多边形裁剪新算法 ［J］.测绘科学，2011，36 （3）：234－235.］

［7］Weiler K，Atherton P.Hidden surface removal using polygon area sorting ［C］／／Proceedings of the SIGGRAPH.New York：ACM Press，1977：214－222.

［8］Vatti B R.A generic solution to polygon clipping ［J］.Communications of the ACM，1992，35 （1）：56－63.

［9］Greiner G，Hormann K.Efficient clipping of arbitrary polygons［J］.ACM Transactions on Graphics，1998，17 （2）：71－83.

［10］LIU Yongkui，GAO Yun，HUANG Youqun.An efficient algorithm for polygon clipping ［J］.Journal of Software，2003，14 （4）：845－856 （in Chinese）.［刘勇奎，高云，黄有群.一个有效的多边形裁剪算法 ［J］.软件学报，2003，14（4）：845－856.］

［11］PENG Jie，LIU Nan，TANG Yuanbin，et al.An efficient algorithm for polygon clipping based on intersection points sorting ［J］.Journal of Zhejiang University （Science Edition），2012，39 （1）：107－111 （in Chinese）.［彭杰，刘南，唐远彬，等.一种基于交点排序的高效多边形裁剪算法 ［J］.浙江大学学报 （理学版），2012，39 （1）：107－111.］

［12］ZHAO Hongbo，ZHANG Han.Algorithm for contour clipping against general polygon window ［J］.Computer Engineering and Applications，2012，48 （32）：170－175 （in Chinese）.［赵红波，张涵.一种等值线图的任意复杂多边形窗口裁剪算法 ［J］.计算机工程与应用，2012，48 （32）：170－175.］

［13］ZHOU Qingping，CHEN Xuegong.Algorithm for contour clipping against general polygon ［J］.Computer and Modernization，2012 （4）：196－200 （in Chinese）.［周清平，陈学工.大规模等值线图任意多边形裁剪算法 ［J］.计算机与现代化，2012 （4）：196－200.］

［14］CHEN Zhanlong，WU Liang，LIU Huanhuan.Simple feature model polygon clipper algorithm base on sorting edges table ［J］.Microelectronics ＆ Computer，2012，29 （9）：145－148（in Chinese）.［陈占龙，吴亮，刘焕焕.基于排序边表的简单要素模型多边形裁剪算法 ［J］.微电子学与计算机，2012，29 （9）：145－148.］

［15］LIU Xuena，HOU Baoming.An improved algorithm for polygon clipping in complex polygon window ［J］.Computer and Modernization，2009 （11）：36－38 （in Chinese）.［刘雪娜，侯宝明.复杂多边形窗口的多边形裁剪的改进算法 ［J］.计算机与现代化，2009 （11）：36－38.］

［16］WANG Jiechen，SHEN Dingtao，CHEN Yanming，et al.An efficient algorithm for complex polygon clipping ［J］.Geomatics and Information Science of Wuhan University，2010，53 （3）：369－372 （in Chinese）.［王结臣，沈定涛，陈焱明，等.一种有效的复杂多边形裁剪算法 ［J］.武汉大学学报（信息科学版），2010，53 （3）：369－372.］

［17］JIANG Ping，LIU Minshi.Improved ray method to judge the relation of point and polygon including simple curve ［J］.Science of Surveying and Mapping，2009，34 （5）：220－222（in Chinese）.［江平，刘民士.射线法判断点与包含简单曲线多边形 关系 的完善 ［J］.测 绘科学，2009，34 （5）：220－222.］

［18］LIU Minshi，WANG Chun.The improved algorithm to determine the inside and outside relationships between point and polygon by ray method ［J］.Journal of Chuzhou University，2010，12 （2）：14－16 （in Chinese）.［刘民士，王春.射线法判断点与多边形内外关系的改进算法 ［J］.滁州学院学报，2010，12 （2）：14－16.］