整体叶盘集成制造单元A 轴的摩擦补偿控制

赵鹏兵，史耀耀，赵 盼

（西北工业大学 现代设计与集成制造技术教育部重点实验室，陕西 西安 710072）

0 引言

整体叶盘是航空航天工业非常关键和重要的零件，其叶片型面的发展趋势为扭角增大、弦宽增加、叶身减薄［1］，叶片轮廓精度向20μm～30μm 水平发展，叶片表面粗糙度已经达到0.4μm～0.6μm，材料加工难度也在不断提高。目前，国产五坐标机床很难满足该类零件的高效精密制造要求，国内在整体叶盘制造工艺与装备方面普遍采用进口通用五坐标机床。另外，国外的整体叶盘制造现已基本形成集粗加工、精加工、自动化抛光、自动化检测和自动化上料于一体的全数字化集成制造单元，实现了整体叶盘的高效率、高质量及低成本制造［2］。为此，自主研发适用于整体叶盘集成制造的高效强力复合铣数控装备，对于支撑该类零件的高精加工及降低制造成本具有重要意义。强力复合铣中的“强力”主要体现在两方面：①将盘铣工艺引入整体叶盘的加工中，而钛合金属于难加工材料，采用大尺寸盘铣刀对叶盘通道进行开槽加工时需要较强的切削力；②进行扩槽加工与曲面成形时采用插铣刀的直径由原来的12mm 增加到20mm，需要采用大功率电主轴来提供较强的切削力。复合铣指盘铣、插铣与侧铣工艺的结合。

叶片轮廓与表面加工精度的提高使其对整体叶盘集成制造装备伺服系统的性能要求也随之提高，A 轴单元作为该集成制造装备的关键功能部件，其定位精度直接影响整体叶盘的加工精度和表面质量。A 轴单元的研究主要以提高运动精度和传动刚度为目标。对于本文所研究的大功率、大扭矩A轴单元，其机械传动系统的非线性摩擦成为影响其运动精度的首要因素。对非线性摩擦进行补偿控制，并使所设计的控制算法具有较强的鲁棒性和抗干扰性，是A 轴单元实现高精度控制的难点所在。对非线性摩擦进行补偿控制已成为精密运动控制研究的热点。文献［3］提出了基于神经网络的混合补偿方法，但混合神经网络模型结构复杂、训练时间长、算法实时性差；文献［4］设计了基于递归模糊神经网络的摩擦补偿策略，并通过李雅普诺夫稳定性理论证明了该控制器的渐进稳定性；文献［5］基于LuGre摩擦模型进行补偿，利用多目标输出反馈控制很好地解决了摩擦模型的变化和不确定参数对定位控制精度的影响；文献［6］将在线辨识与自适应控制相结合，通过自适应调节控制输入来补偿摩擦和齿隙非线性，并通过调整模糊控制参数保证系统的稳定性；文献［7］采用基于干扰观测器的滑模控制，其中滑模控制保证了控制系统的鲁棒性，干扰观测器估计外部扰动并生成补偿信号以抑制外部扰动；文献［8］通过对跟踪误差的测量数据进行分析，建立了相应的摩擦补偿模型，但是该方法的通用性不强；文献［9］利用模糊推理系统自适应学习被控对象的未知摩擦行为，并对其进行补偿，有效提高了系统速度突变时的跟踪精度，但单纯地采用模糊推理系统在提高控制精度和系统稳定性方面还有待作进一步改进。

为此，本文以自主研制的大功率、大扭矩、高刚度A 轴单元为研究对象，针对静态和动态摩擦模型的不同动力学特性，提出两种不同的积分型滑模控制器。根据不同的摩擦阶段，相应的摩擦补偿控制器被激活，两种摩擦状态系统在运动过程中不断切换，同时摩擦补偿控制器也在不断切换。积分型滑模控制的引入很好地消除了传统滑模控制的抖振现象，有效提高了A 轴单元的定位精度和跟踪精度，采用该摩擦补偿控制算法加工后的整体叶盘，其表面粗糙度、型面尺寸平均误差和表面波纹度均显著减小。

1 整体叶盘集成制造工艺及A轴设计

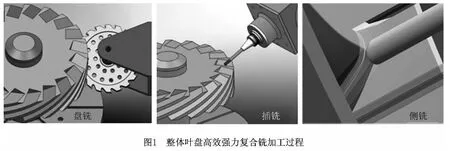
针对目前整体叶盘制造效率低、精度低、成本高等问题，本文在分析已有加工方法的基础上，结合整体叶盘的结构特点，提出一种高效强力复合铣集成制造工艺，即盘铣—插铣—侧铣复合加工。在此基础上，将盘铣、插铣与侧铣等加工工艺高度集成于一台数控设备中，研制了整体叶盘高效强力复合铣数控机床。该工艺的加工过程是：①利用盘铣切削效率高的特点对叶盘通道进行开槽，最大限度地去除材料；②通过插铣工艺对盘铣不可达区域（切削干涉区域）进行高效插铣，实现扩槽加工与曲面成形；③使用圆柱铣刀或球头铣刀进行侧铣，实现除棱清根。整个加工过程如图1所示。该加工过程中，盘铣与插铣阶段属于高效强力切削，侧铣阶段属于半精加工，插铣与侧铣功能主要由A 轴单元实现。自主研制的高精度、大扭矩、高刚度A 轴单元如图2所示，其中左主轴、主轴箱、右主轴通过左右两侧的转台轴承固定在一起。伺服电机安装在箱体上端的右后方，箱体右侧内由蜗轮及可调整反向间隙的双导程蜗杆构成传动机构。旋转轴端内置高分辨率角度编码器，可实现A 轴的闭环控制。箱体左侧内有液压锁紧机构，可将旋转轴在任意位置锁紧。主轴水平状态为零点，可向上摆动30°，向下摆动120°。

如图3所示，该A 轴控制系统的总体结构主要由研华IPC-610-H 工业控制机（上位机）、Turbo PMAC Clipper运动控制器（下位机）、伺服驱动器、西门子1FT7105型永磁同步交流电机、梯形齿同步带、蜗轮蜗杆、电主轴和海德汉RCN829±1″角度编码器构成。该系统利用角度编码器对电主轴的摆动角位移进行测量，并将其反馈给控制器，控制系统在每个采样周期内根据测量系统的反馈数据和系统指定输入计算电主轴摆动的角度偏差，并按照程序给定的控制算法计算控制输出量。控制器发出的控制指令通过D／A 转换器和伺服驱动器驱动交流电机，再由电机转矩通过同步带和蜗轮蜗杆机构驱动电主轴摆动，以实现零件加工所需的主轴摆动角位移。

2 摩擦模型描述

2.1 静态摩擦模型

为了较好地描述该大功率、大扭矩A 轴的静态摩擦动力学，这里采用一种新的静态摩擦模型［10］，该模型结合了静摩擦的两个重要特征——滞环和塑性，它由非线性弹性模块和塑性模块两个模块构成。由于这两个模块的作用，当给A 轴施加驱动力矩时，相应地会产生摩擦力矩。

令σs为A 轴所受的外力矩，θs为扭转弹性角位移，则非线性弹性效应可描述为

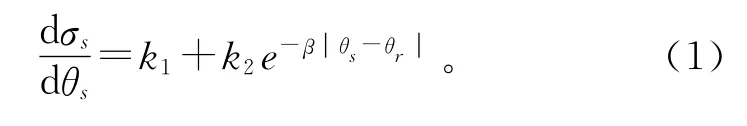
式中：k1，k2和β为正标量，θr为相关联的反向运动点处的角位移。式（1）与文献［10］中所述的反向点规则相结合便产生了滞环。

为了更好地描述塑性行为，引入了一种硬化状态θh。令σ为所施加的外力矩，θp为塑性变形，则塑性行为可描述为

式中f（|σ|）=|σn|／λ，α，λ和n 为正标量。

这样，静摩擦可分为爬行阶段和硬化阶段。根据文献［10］，静摩擦的动力学特性可用五种状态来描述，给控制器的设计带来不便，通过引入sgn（·）函数可得到如下简洁的状态方程表达式。

（1）爬行阶段（|σn|／λ＞θh）

（2）硬化阶段（|σn|／λ≤θh）

式中Cs为系统的等效阻尼系数。测得A 轴的输出角位移θ为

将以上各式与反向点规则结合，可得A 轴在静摩擦作用下的输出响应。公式中各参数值可根据文献［10］所述的测试方法进行参数辨识。本文从多组实验数据中选择了一组有代表性的值（如表1），用于A 轴传动系统中静摩擦补偿控制器的设计。

表1 静摩擦模型参数

2.2 动态摩擦模型

为了描述A 轴的动态摩擦行为，本节采用LuGre摩擦模型［11］，表述如下：

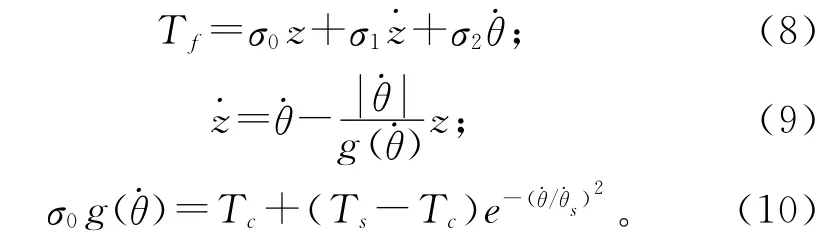
在摩擦力矩Tf的作用下，A 轴的动力学方程为

式中：θ为输出角位移，J 为转动惯量。

式（8）～式（10）中的参数值可根据文献［11］所述的实验方法进行辨识。通过测量多组施加给A轴的力矩及相应的A 轴角速度可得所需的实验数据，角速度可通过对角度编码器测得的角位移进行微分得到。通过对测试数据进行统计分析便可提取出摩擦响应的特征曲线，辨识所得参数值如表2所示。

表2 动摩擦模型参数

3 滑模控制器设计

3.1 基于静摩擦模型的滑模控制器设计

由于该静摩擦模型较为复杂，本节考虑采用一个名义线性系统，由式（7）得：

将式（12）代入式（3）和式（4），可以得到只包含测量状态的子系统，表达如下：

（1）爬行阶段

（2）硬化阶段

如果用一个“二阶线性转动惯量—旋转阻尼—扭转弹簧系统”（JCK）来名义上描述式（13）和式（14）的输出动态特性，则其可以描述为［12］：

（1）爬行阶段

（2）硬化阶段

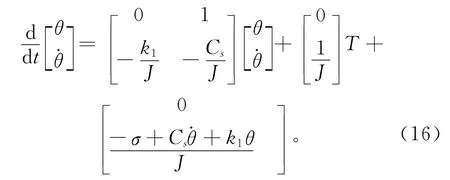
名义JCK 的刚度系数和阻尼系数的选择与式（5）和式（6）中的k1和Cs相同，等式右端的其他项可认为是系统干扰或偏差。

为了达到跟踪控制的目的，采用偏差描述系统的表达式，定义偏差为e=θ-θd，θd为期望的A 轴角位移，并假定其对时间二阶可导。

将式（17）代入式（15）和式（16），可得：

（1）爬行阶段

（2）硬化阶段

将式（18）和式（19）表达为如下通式：

现针对式（20）所表达的系统设计滑模控制律。

定义滑模面s为［13］

当s=0时，闭环系统方程变为

定义切换控制律为［14］

因此，滑模控制律为

3.2 基于动摩擦模型的滑模控制器的设计

基于摩擦估计的动态摩擦补偿策略在许多运动控制的研究中已有报道，本文采用基于LuGre动态摩擦模型的离线摩擦估计策略对动态摩擦力矩进行预补偿，如图4所示。由于估计误差，经前馈补偿后的系统动力学方程可表述为

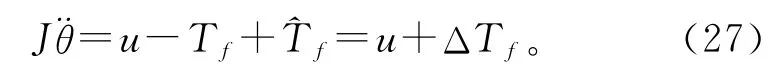
式中ΔTf=-Tf，表示摩擦力矩估计误差。

定义e=θ-θd和=-，式（27）可表述为

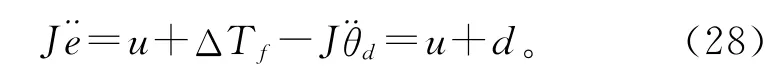
式中d=ΔTf-为系统所受干扰。式（28）可用如下状态方程描述：

定义滑模面方程为［15］

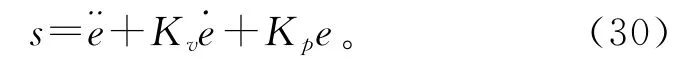
滑模控制律为

将式（31）代入式（28），根据滑模面的定义可得闭环系统方程为

这表明闭环系统的特征主要取决于式（32）。相应的滑模到达条件可由公式

针对动静态摩擦模型分别设计了两个相应的摩擦补偿控制器，整个A 轴系统的摩擦补偿控制策略如图5所示。根据摩擦学研究报告可知，这两个控制器的切换标准是一个非常复杂的问题。本文采用的方法是：通过交流伺服电机对A 轴系统由零开始逐步加载，记录电主轴由静止状态进入运动状态时角度编码器的读数，重复测量10组数值，最终取其平均值4.848×10-4°作为切换标准。

通过对控制系统进行多次调试，取表3所示的控制器参数。

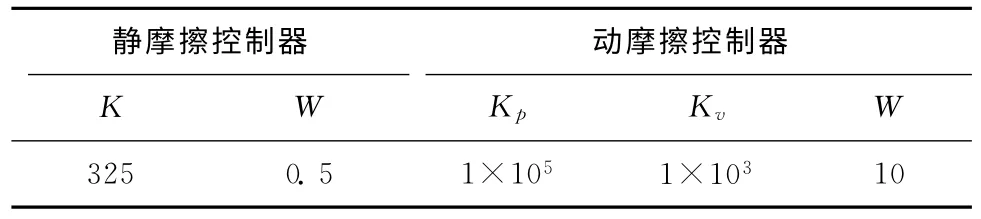
表3 控制器参数

4 实验验证

该实验采用研华IPC-610-H 工控机为上位机，主要进行控制程序的编辑和执行，实现人机交互并通过运动控制器实现整体叶盘加工过程中各种运动的控制；采用可编程多轴控制器（Program Multiple Axises Controller，PMAC）作下位机，直接控制伺服驱动器驱动交流电机完成各种所需运动，并监控运动过程中各状态量的变化；基于C++语言编写控制程序，包括摩擦补偿控制程序、数字信号和模拟信号的转换程序、控制系统的采样程序和角度编码器的测量程序等；采用研华PCL818L 数据采集卡、PCL730隔离数字量I／O 卡、PCL726模拟量输出卡进行数据的采集、转换和输出［16］。

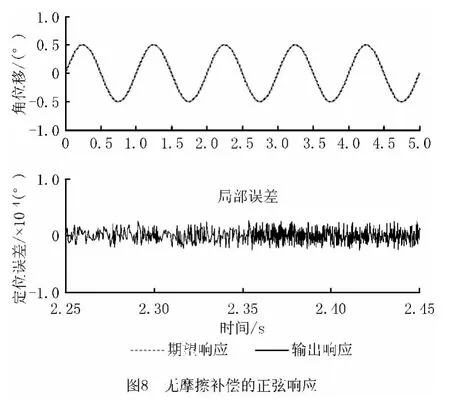
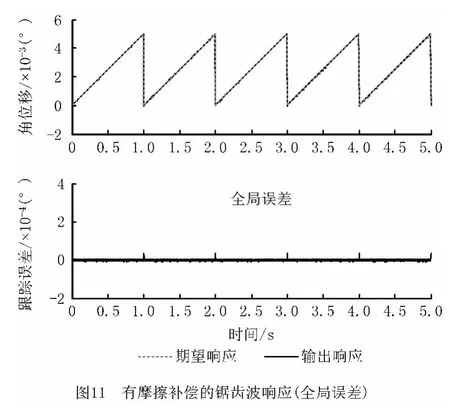
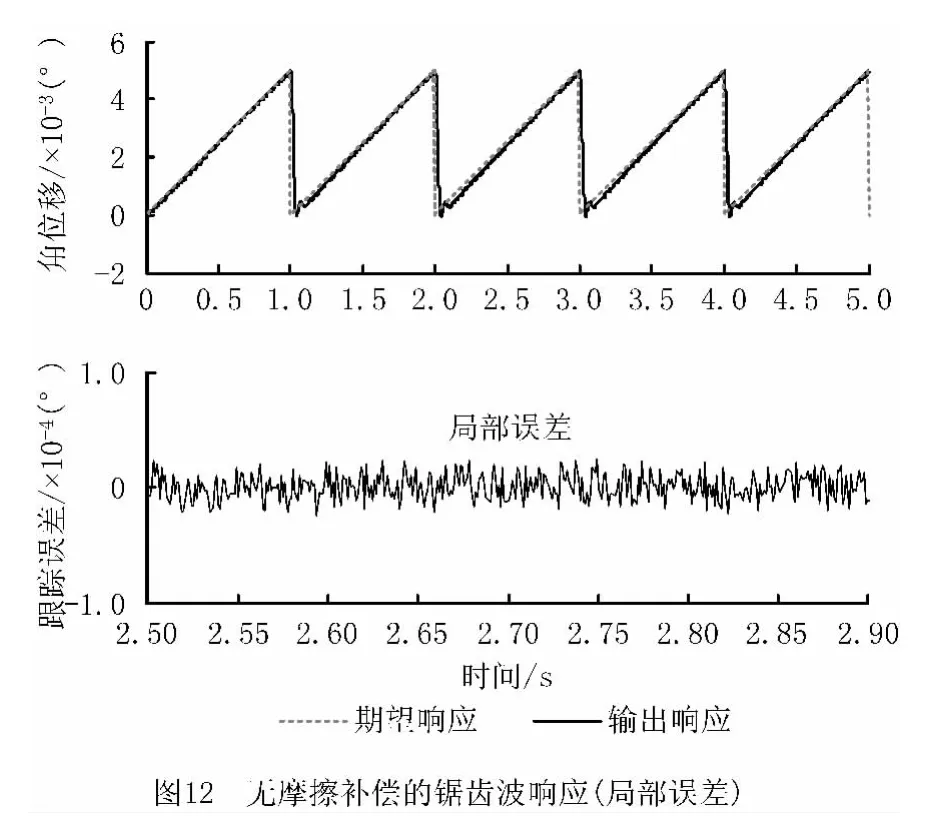
首先给系统施加r（t）=0.005°的阶跃信号以检验其定位控制性能，通过角度编码器测量系统在给定信号下的实际输出值，将实际输出值与给定信号值相减，便可得到系统的转角误差。由图6 和图7可知，受非线性摩擦干扰，系统稳态误差较大，通过摩擦补偿，稳态误差减小了69.51%。接着，采用r（t）=0.5sin（2πt）的正弦信号检验系统的跟踪控制性能，由图8和图9可知，通过采用摩擦补偿控制，系统的动态误差减小了65.11%，由此说明非线性摩擦是影响A 轴定位精度的主要因素。最后，为检验系统在恶劣工况下的工作性能，对其施加了幅值为0.005°、周期为1s的锯齿波信号，由图10和图11可知，受非线性摩擦影响，当控制信号由最大值陡落至0时，系统跟踪性能恶化，通过摩擦补偿，下降沿跟踪误差减小了85.86%。图12和图13为锯齿波上升过程中的跟踪误差对比，经摩擦补偿，信号上升阶段的跟踪误差减小了69.77%。表4所示为不同控制信号在有无摩擦补偿时的控制误差比较。由以上分析可知，采用基于摩擦模型的滑模补偿控制后，A 轴系统的定位精度大幅提高，但补偿后系统控制误差并没有完全消除，主要因为除了非线性摩擦干扰外，系统的控制精度还受反向间隙、参数摄动、测量噪声等的影响。

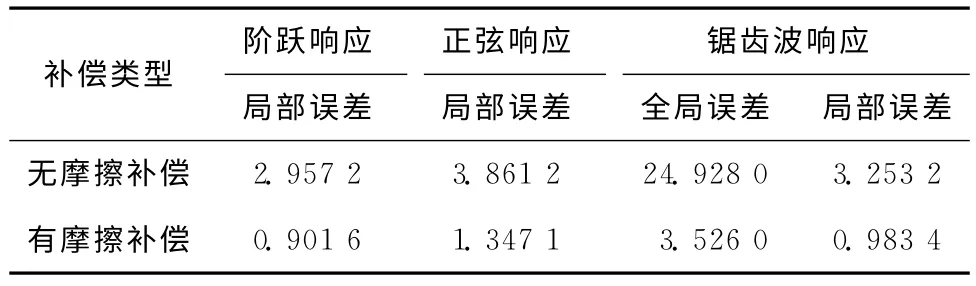
表4 控制误差比较 10-5（°）

为了进一步检验该摩擦补偿控制算法的有效性，在自主研制的整体叶盘高效强力复合铣集成制造单元上进行了加工实验。被加工的整体叶盘相关参数如下：外径318 mm、通道深度98 mm、通道最窄宽度22.3mm、通道数目20。采用直径Φ=160 mm、切宽d=20mm、齿数N=14的盘铣刀对叶盘通道进行开槽，径向切削深度ae=20mm，主轴转速n=100r／min，进给速度vf=60 mm／min，进给量fz=0.06mm；采用直径Φ=20mm、齿数N=2的K40整体硬质合金平底铣刀进行插铣，以实现扩槽加工与曲面成形，轴向切削深度ap=18 mm，径向切削深度ae=3mm，主轴转速n=1 600r／min，进给速度vf=200mm／min，进给量fz=0.08mm；采用刃径R=8 mm、柄径Φ=16 mm、刃长lr=32 mm、总长l=100mm、齿数N=3的硬质合金球头铣刀进行侧铣，径向切削深度ae=2.5mm，主轴转速n=2 000r／min，进给量fz=0.05mm，侧铣加工时根据刀具伸长量的大小变化，进给速度在vf=50 mm／min～100mm／min范围内波动。

采用DEA DELTA Slant三坐标测量仪对叶片型面尺寸平均误差和叶片表面波纹度进行测量，叶片型面尺寸平均误差指叶片轮廓平均误差，即实际测量的加工曲面与理论曲面之间的平均差异度。采用Taylor-hobson粗糙度仪对叶片表面粗糙度进行测量。图14和图15分别为未采用摩擦补偿和采用摩擦补偿加工后的整体叶盘，叶片表面质量性能指标的测试结果如表5所示。可见，加工后的表面波纹度减小了40.58%，型面尺寸平均误差减小了41.85%，表面粗糙度减小了38.60%。加工实验结果进一步证明了所设计的摩擦补偿控制算法的有效性和可行性。

表5 整体叶盘加工效果对比

5 结束语

本文针对目前整体叶盘制造效率低、精度低、成本高等问题，在分析已有加工方法的基础上，结合整体叶盘的结构特点，提出一种高效强力复合铣集成制造工艺，即盘铣—插铣—侧铣复合加工，阐述了自主研制的大功率、大扭矩、高刚度A 轴的结构组成及其控制系统工作原理，分析了静态和动态摩擦模型的动力学特性，并通过实验对摩擦模型进行了参数辨识。采用“二阶线性转动惯量—旋转阻尼—扭转弹簧系统”对复杂的静态摩擦模型进行了简化。根据静态和动态摩擦模型的不同动力学特性，设计了两种不同的积分型滑模控制器，并通过实验验证了该摩擦补偿控制器的有效性和可行性。

［1］DUAN Jihao，SHI Yaoyao，LI Xiaobiao，et al.Study on adaptive polishing method of flexible grinding head for blisk［J］.Acta Aeronautica et Astronautica Sinica，2011，32（5）：934-940（in Chinese）.［段继豪，史耀耀，李小彪，等.整体叶盘柔性磨头自适应抛光实现方法研究［J］.航空学报，2011，32（5）：934-940.］

［2］OLIVEIRA J F G，SILVA E J，GUO C，et al.Industrial challenges in grinding［J］.CIRP Annals-Manufacturing Technology，2009，58（2）：663-680.

［3］CILIZ M K，TOMIZUKA M.Friction modeling and compensation for motion control using hybrid neural network models［J］.Engineering Applications of Artificial Intelligence，2007，20（7）：898-911.

［4］HAN S I，LEE K S.Robust friction state observer and recurrent fuzzy neural network design for dynamic friction compensation with backstepping control［J］.Mechatronics，2010，20（3）：384-401.

［5］KHAYATI K，BIGRAS P，DESSAINT L.LuGre model-based friction compensation and positioning control for a pneumatic actuator using multi-objective output-feedback control via LMI optimization［J］.Mechatronics，2009，19（4）：535-547.

［6］SURANENI S，KAR I N，RAMANA O V，et al.Adaptive stick-slip friction and backlash compensation using dynamic fuzzy logic system［J］.Applied Soft Computing，2005，6（1）：26-37.

［7］ALTINTAS Y，VERL A，BRECHER C，et al.Machine tool feed drives［J］.CIRP Annals-Manufacturing Technology，2011，60（2）：779-796.

［8］XI Xuecheng，POO A N，HONG G S.Tracking error-based static friction compensation for a bi-axial CNC machine［J］.Precision Engineering，2010，34（3）：480-488.

［9］GARAGIC D，SRINIVASAN K.Adaptive friction compensation for precision machine tool drive［J］.Control Engineering Practice，2004，12（11）：1451-1464.

［10］HSIEH C，PAN Y C.Dynamic behavior and modeling of the pre-sliding static friction［J］.Wear，2000，242：1-17.

［11］XIANG Hongbiao.Research on model and compensation for open servo system［D］.Tianjin：Tianjin University，2010：22-25（in Chinese）.［向红标.开放式伺服系统的摩擦建模与补偿研究［D］.天津：天津大学，2010：22-25.］

［12］YANG Yiyong，JIN Dewen.Mechanical system dynamics［M］.Beijing：Tsinghua University Press，2009：24-37（in Chinese）.［杨义勇，金德闻.机械系统动力学［M］.北京：清华大学出版社，2009：24-37.］

［13］YAO Qionghui，HUANG Jiqi.Variable structure control systems［M］.Chongqing：Chongqing University Press，1997：14-28（in Chinese）.［姚琼荟，黄继起.变结构控制系统［M］.重庆：重庆大学出版社，1997：14-28.］

［14］XI Xuecheng，HONG G S，POO A N.Improving CNC contouring accuracy by integral sliding mode control［J］.Mechatronics，2010，20（4）：442-452.

［15］CHEN C L，LIN C J.A sliding mode control approach to robotic tracking problem［C］／／Proceedings of the 15th IFAC World Congress.Munich，Germany：IFAC，2002：21-26.

［16］LI Maoyue，FU Hongya，HAN Zhenyu.Design and machining for open intelligent controller［J］.Computer Integrated Manufacturing Systems，2011，17（7）：1441-1447（in Chinese）.［李茂月，富宏亚，韩振宇.开放式智能控制器的设计与加工实现［J］.计算机集成制造系统，2011，17（7）：1441-1447.］