基于附着系数曲线长度的路面识别仿真研究

张晓龙，孙仁云，林小龙，李锋

（西华大学 交通与汽车工程学院，四川成都610039）

不少学者将μ（s）曲线小滑移率阶段的斜率作为参数指标进行路面识别[1-2]，但是某些滑移率下μ（s）曲线斜率存在重叠相等的情况，所以只有在曲线斜率μ（s）差别明显的个别滑移率下才能完成识别，也就是通过曲线在个别点上的斜率特征进行识别。但是车辆制动时μ（s）曲线斜率可能出现波动，通过曲线上个别点的斜率进行识别可能产生错误识别。曲线的轨迹是由曲线上各点的斜率共同作用形成的，如果能将曲线某个区间上每个点的斜率特征作为识别参数将显著增加识别的可靠性。

1 轮胎模型及路面信号发生器

Kiencke等人在大量路面试验数据的基础上提出了一种实用的μ（s）（附着系数—滑移率）曲线，曲线方程如下[3]：

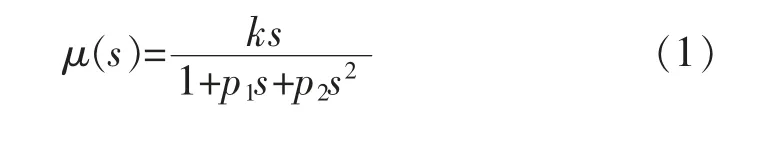
式中：k为μ（s）曲线斜率，一般取30；各路面的p1和p2值见表1。采用求极值的方法可以求出各路面最佳滑移率s0，见表1。

根据表1中p1和p2的值得到7种典型路面的μ（s）曲线，如图1所示。计算机仿真时利用此模型产生路面信号。

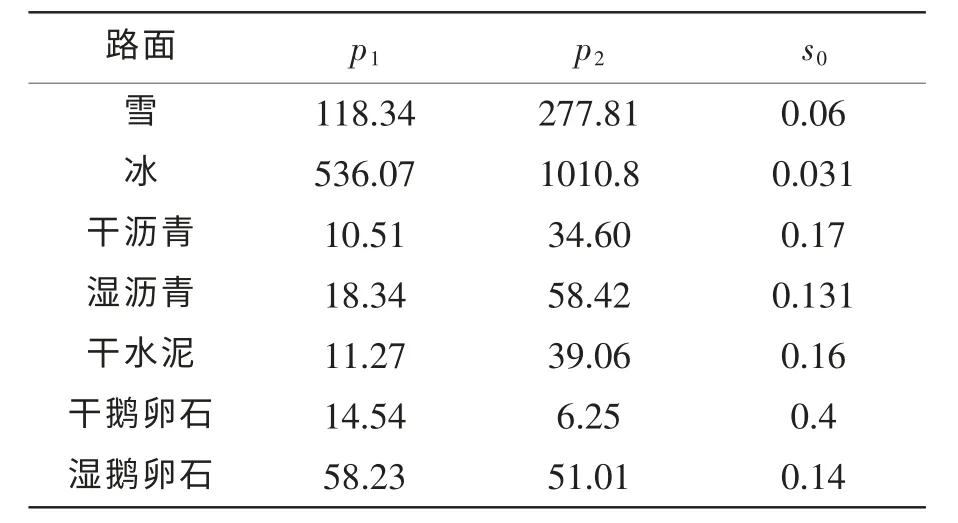
表1 轮胎模型中各典型路面参数值及最佳滑移率

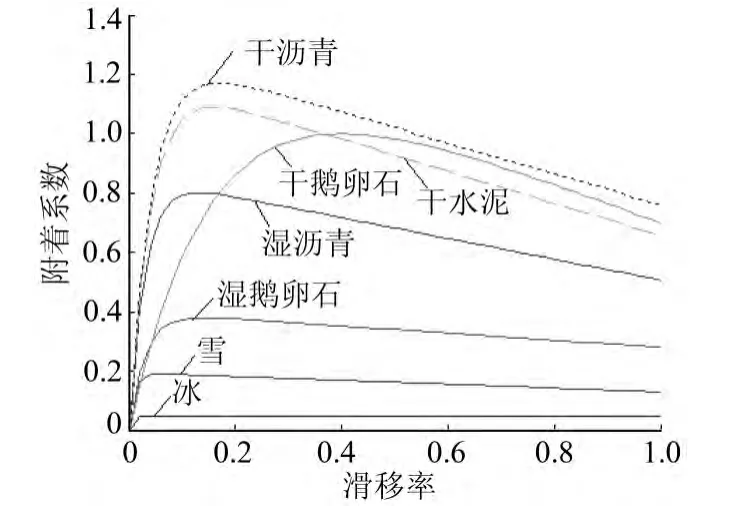
图1 典型路面的μ（s）曲线

2 路面状态自动识别方法

滑移率区间[0，b]上附着系数曲线长度为[4]

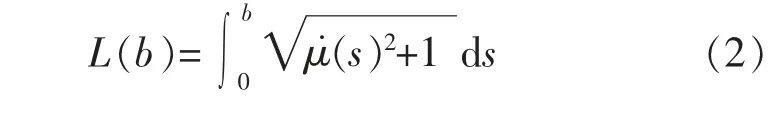
式中：μ（s）为附着系数曲线μ（s）的斜率。计算 L（b）时需要用到μ（s）曲线在滑移率区间[0，b]上每个点的斜率，所以L（b）包含 μ（s）曲线在滑移率区间[0，b]上每个点的斜率特征。如果把L（b）作为路面识别的参数指标，就等于间接将μ（s）曲线在滑移率区间[0，b]上每个点的斜率特征作为识别的参数指标。

将区间[0，b]分为n等份，则

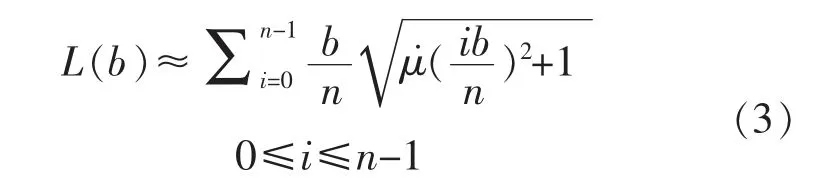
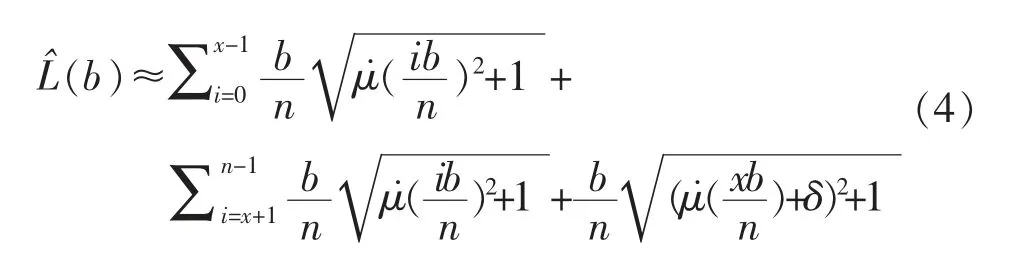
则有

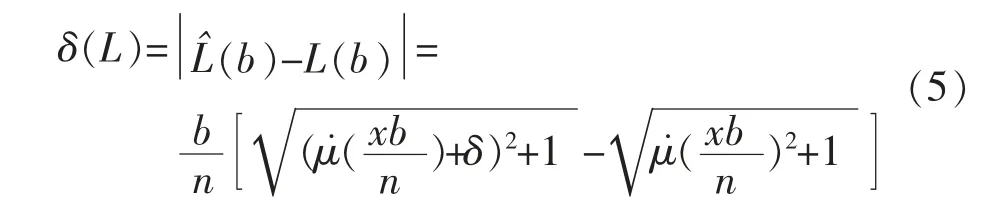
显然 limn→∞δ（L）＝0，所以随着采样点数的增加，个别点上曲线斜率的误差对曲线长度的影响越来越小。

综上所述，相比曲线斜率μ（s），曲线长度 L（s）作为参数指标进行路面识别的可靠性和抗干扰性更强。

由式（1）得

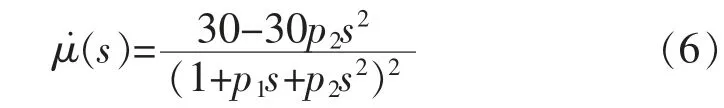
由式（2）和式（6）得

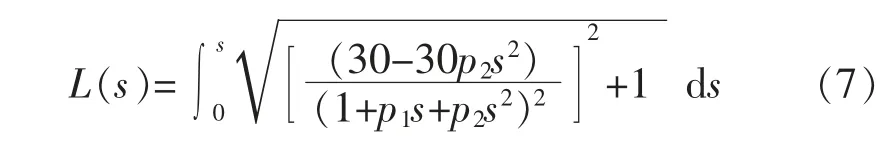
根据表1中的参数值可以计算各典型路面不同滑移率下的曲线长度，如图2所示。可以看出：当s＝0.1时，各典型路面附着系数曲线长度 L（0.1）差距明显，易于识别，同时考虑到干沥青和干水泥路面特性相似，可合而为一，因此可以将L（0.1）作为参数指标进行路面识别。

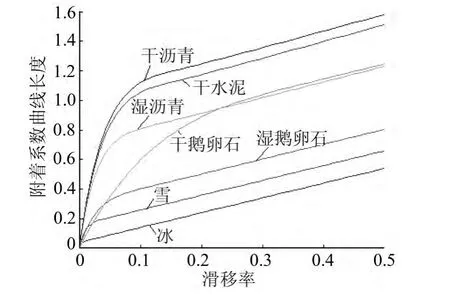
图2 典型路面附着系数曲线长度—滑移率关系图

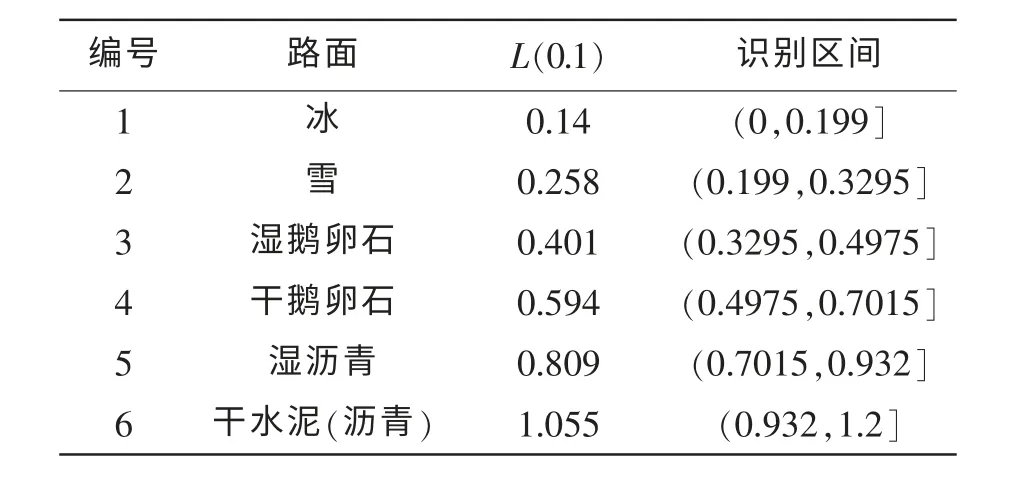
表2 各典型路面的L（0.1）和识别区间

2.1 典型路面识别区间

由式（7）和表1中的参数值计算出各典型路面的，根据L（0.1）划分6种典型路面的识别区间同时对路面进行编号，如表2所示。

2.2 附着系数曲线斜率的估算

前文定义的L（s）的算法中包含对附着系数曲线斜率μ（s）的估算。从式（8）可以看出，只要求出附着系数对时间的导数（t）和滑移率对时间的导数（t），即可求出（s）。忽略车轮滚动阻力，对车轮进行受力分析可得

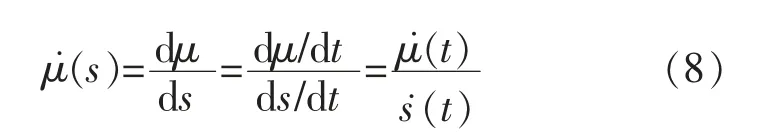
在已知车轮的角加速度、车轮制动器制动力矩、车轮受到的来自地面的法向作用力等的基础上，通过式（9）能够快速估算出当前路面实时的路面附着系数μ。

根据式（10）可求出s：

式中：V为车辆行驶速度，通过一定方法估计或相关传感器测得；ω为车轮转速，通过轮速传感器测得。

分别对μ和s 差分得到μ（t）和s（t），根据式（8）计算出μ（s）。

2.3 附着系数曲线长度的识别算法

在进行识别前，系统默认当前路面为路面6，即实时控制的目标滑移率初始值为0.16。当驾驶员踩下制动踏板后，制动踏板输入一定开度，汽车开始制动，滑移率从0 开始向0.16快速递增，实时估算μ（s），同时将与该时刻滑移率增量（当前滑移率与前一时刻滑移率之差）相乘，并将计算结果不断累加，当滑移率等于0.1时，完成累加，得到实时路面的L（0.1）。同时判断当前路面的L（0.1）落入哪一个识别区间，从而完成路面识别，并将识别路面的最佳滑移率作为控制器实时控制的目标滑移率。

2.4 跃变路面的识别算法

考虑到汽车大部分时间行驶在干沥青（水泥）路面上，所以制动过程中路面跃变为湿沥青路面的可能性最大，同时当滑移率等于0.131（湿沥青路面的最佳滑移率）时，各典型路面的附着系数差距明显，利于识别。所以当制动过程中路面发生跃变后，默认路面跃变为路面5（湿沥青），实时控制的目标滑移率立即调整为0.131，当实际滑移率调整到0.131附近时，判定当前路面的附着系数落入哪个具体的识别区间从而完成路面识别，并将识别路面的最佳滑移率作为控制器实时控制的目标滑移率。各典型路面的μ（0.131）及其识别区间如表3所示。

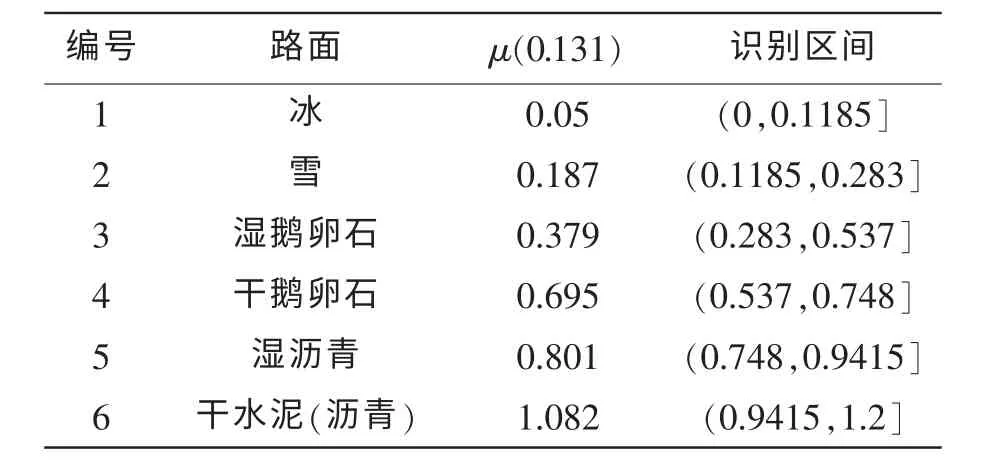
表3 各典型路面的μ（0.131）和识别区间

3 仿真试验

在制动单轮模型的基础上，以30 m·s-1的初速度制动，使用Matlab/Simulink软件在跃变路面上进行模拟试验。图3为路面识别仿真模型。采用PID控制器进行控制。

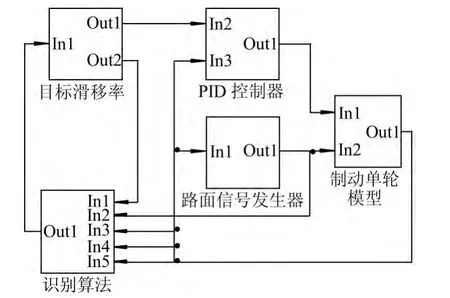
图3 路面识别仿真模型

3.1 制动单轮模型

为了简化问题，忽略侧向力、空气阻力以及车轮滚动阻力的影响，假设路面平直，采用制动单轮模型进行分析，如图4所示。式（11）为车辆方程，式（12）为车轮方程[5]。

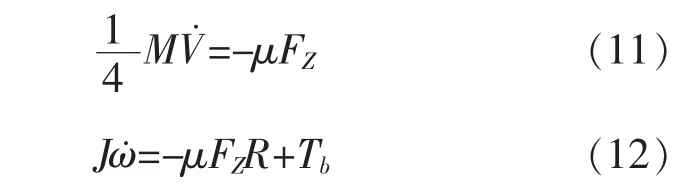
式中：M为车辆的质量；V为车辆的减速度；μ为路面的附着系数；FZ为车轮受到来自地面的法向作用力，通过加速度传感器及理论分析可得到；J为车轮的转动惯量，通常认为是常数；R为车轮的滚动半径；为车轮的角减速度，通过ABS 装备的轮速传感器可得到；Tb为车轮制动器的制动力矩，通过制动轮缸的压力进行计算，制动轮缸的压力可以通过压力传感器得到[6]。

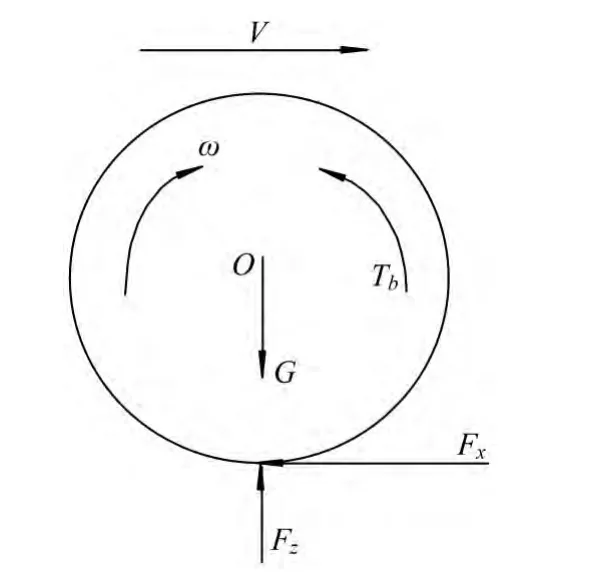
图4 制动单轮模型

3.2 路面识别仿真结果及分析

如图5所示，制动开始时预设路面为路面3，1s后跃变为路面6。

路面识别仿真结果如图6所示。制动开始时默认当前路面为路面 6（干沥青、水泥），0.025 s时识别出当前路面为路面3，1 s时路面跃变为路面6，系统默认跃变为路5（湿沥青），1.01 s时准确识别出路面跃变为路面6。

图7为滑移率—制动时间曲线，1s时路面状态发生变化，完成识别后目标滑移率及时调整，实际滑移率对最佳滑移率的跟踪快速准确，控制效果良好。

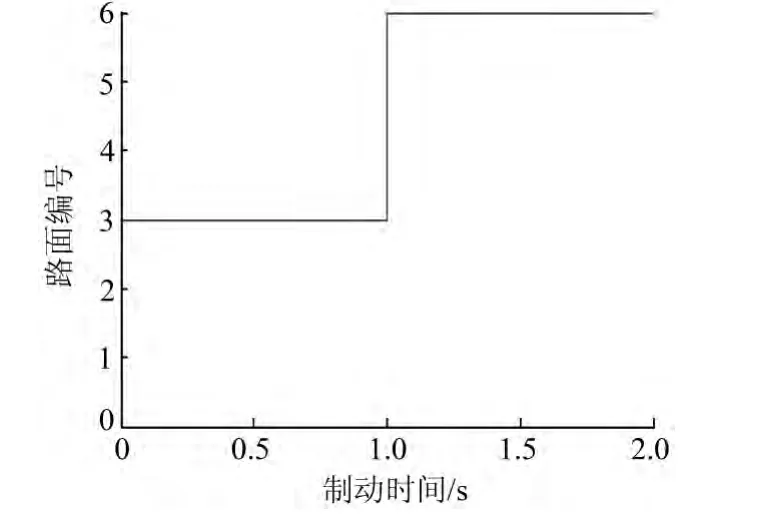
图5 预设路面—时间曲线

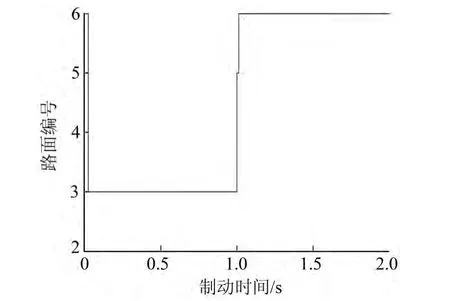
图6 路面识别仿真结果

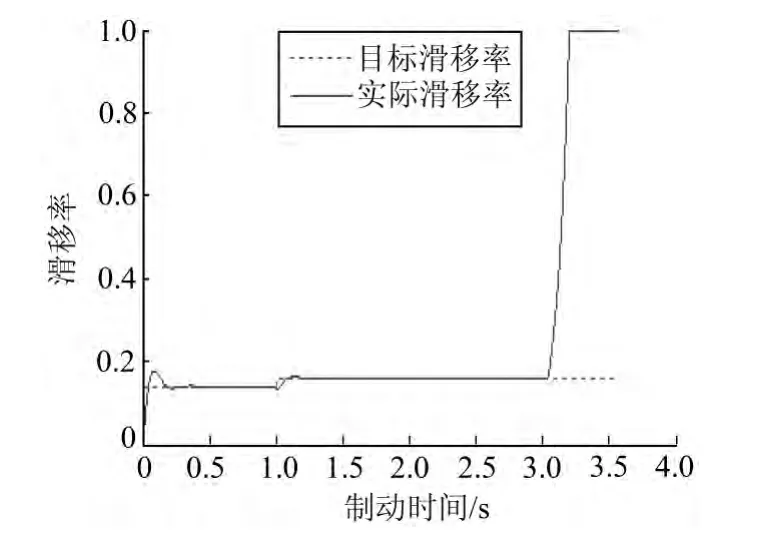
图7 滑移率—制动时间曲线

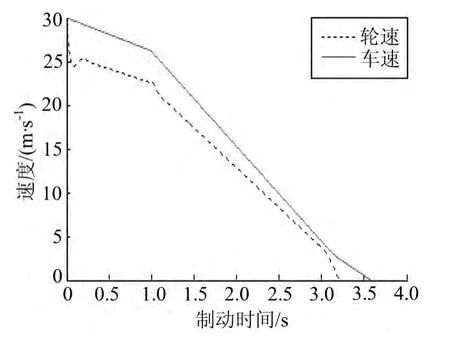
图8 速度—制动时间曲线

图8为速度—制动时间曲线，1 s时路面状态发生变化，从 3.05 s（车速等于4 m·s－1）开始，ABS系统不再起作用，轮速迅速减小，3.2 m·s－1时车轮抱死，3.6 s时制动完成。在ABS系统作用过程中，车轮没有出现抱死，充分利用了当前路面的附着条件，缩短了制动时间，制动效果良好。

4 结论

以7种典型路面在滑移率区间[0，0.1]上的附着系数曲线长度L（0.1）作为参数指标进行路面识别，与通过附着系数曲线个别点上的斜率进行路面识别的方法相比，L（0.1）包含了μ（s）曲线在滑移率区间[0，0.1]上每个点的斜率特征，可靠性更强。同时附着系数曲线上个别点的斜率出现误差对L（0.1）的影响很小，该识别方法的准确性和抗干扰性更强。通过仿真结果可以看出：各典型路面的识别时间均非常短，充分利用了路面的附着条件，提高了制动效能。

[1]Fredrik Gutafsson.Slip－based Tire－road Friction Estimation[J].Auromaricu，1997，33：1087－1099.

[2]Hideo Sado，Shin－ichiro Sakai，Yoichi Hori.Road Condition Estimation for Traction Control in Electric Vehicle[C].IEEE International Symposium on Industrial Electronics，1999：973 － 978.

[3]Kinche U，Dasis A.Estimation of Tyre Friction for Enhanced ABS－Systems[C].Tokyo：Proc.Aveg Congress，1994.

[4]同济大学数学系.高等数学（上册）[M].6版.北京：高等教育出版社，2007.

[5]余志生.汽车理论[M].4版.北京：机械工业出版社，2008.

[6]王博，孙仁云.基于状态特征因子的路面识别方法研究[J].汽车工程，2012，34（6）：506－510.

[7]王博.在线跟踪时变最佳滑移率的汽车 ABS 仿真[J].湖北汽车工业学院学报，2011（1）：1－5.