基于矩阵的多段支持度关联规则挖掘算法

张伟丰，杨丽华

（湖北汽车工业学院 经 济管理学院，湖北十堰442002）

关联规则作为一种重要的数据挖掘算法在商品零售领域的数据分析中获得了比较广泛的应用，经典的Apriori算法采用一种逐层搜索的迭代方法自下而上的寻找频繁集，在数据量比较大的情况下，算法需要反复扫描数据库，产生规模庞大的候选集，运行效率低下，影响其实际应用。为了提高算法的效率，出现了很多改进的算法，比较典型的有增加了事务标识的AprioriTid算法、频繁模式增长的FPGrowth算法、基于多段支持度的算法[1]（大项目集生成算法 Large Items Generation，LIG算法）以及基于矩阵计算的算法[2]，另外，出于处理大型数据库的需要，相继提出了数据分割、多支持度、数据采样等方法，这些改进一定程度上提高了算法运行效率。

为了进一步提高关联规则挖掘算法的效率，笔者在上述研究成果的基础上，提出了基于矩阵的多段支持度关联规则挖掘算法，算法采用分段计算支持度的方式，能使一次扫描数据库获得更多的信息，利用其重要性质来减少候选集的产生，同时将数据初始化为矩阵，利用矩阵进行支持度的计算，避免了多次扫描数据库。

1 多段支持度的基本思想和重要性质

多段支持度是把一个项集的支持度分段计算，每一个段记录该项集在相应规模事务中的支持度，利用其性质及时剔除不能连接生成频繁集的项集，缩减候选集规模[1]。

1.1 多段支持度定义

令数据事务规模 p∈[k，q]，项集 I的支持度为Sp，当k≤p＜q时，Sp为项集 I在规模为p的事务中出现的次数，当p＝q时，Sp为项集 I在规模不低于p的事务中出现的次数，则向量（Sk，Sk+1，…，Sq-1，Sq）称为项集I的多段支持度，则项集I的总支持度按式（1）计算：

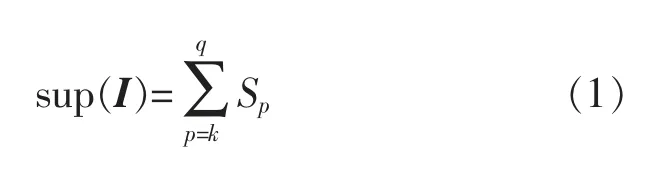
1.2 重要性质[2]

多段支持度关联规则挖掘算法可以利用如下4个性质提高运行效率：

1）频繁集的子集必为频繁集，非频繁集的超集必为非频繁集。

2）对于项集L，在一个已知事务数量的数据集D中，规模小于的事务不会影响其支持度计算。

3）已知数据集D中的一个频繁k项集Lk

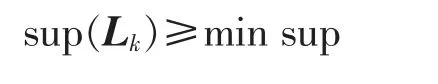
令数据集

若

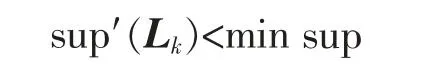
则对D中的任意一个频繁m项集Lm而言，一定有Lk⊄Lm。

4）若频繁k项集 Lki和Lkj的多段支持度分别为（ik，ik+1，…，iq）和（jk，jk+1，…，jq），满足

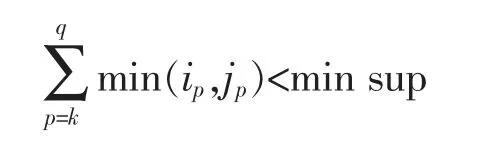
且

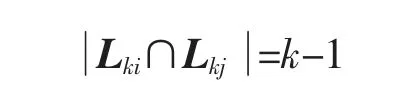
则不能由Lki和Lkj构成候选集Ck+1中的元素。

其中性质 1）、3）、4）减少候选集生成数量，性质2）缩小事务数据集的大小。

2 多段支持度关联规则算法

算法的基本思想是通过一次数据库扫描将事务数据转换为0-1 矩阵的形式，利用矩阵的直接计算特性来计算支持度，产生候选集和频繁集，同时根据多段支持度的性质快速高效地找到频繁集。

2.1 事务数据集的矩阵表示形式及支持度计算

令项的集合 I＝｛I1，I2，…，In｝，事务数据的集合

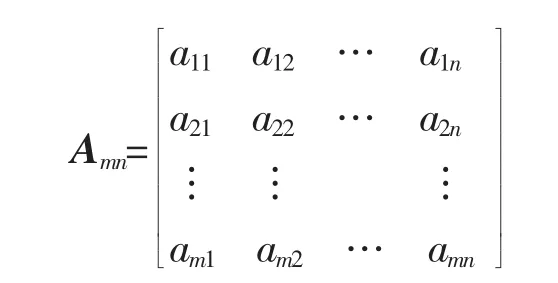
D＝｛D1，D2，…，Dm｝，则数据集可以用项的矩阵表示：

其中，aij∈I或aij＝0（0≤i≤m，0≤j≤n），为方便计算

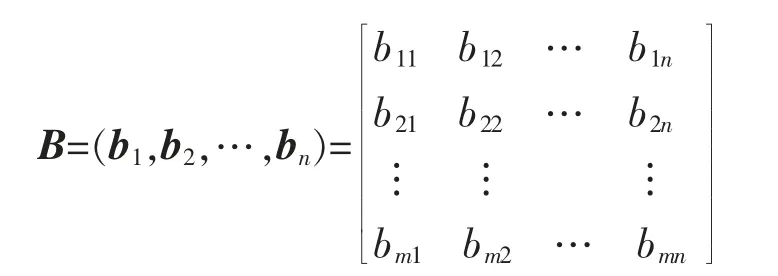
支持度，同时将数据集用计数矩阵B表示：

其中，若 Ij项在事务 Di中出现，则 bij＝1，否则，bij＝0。用向量C 记录事务数据集各事务的规模以用于分段支持度的计算：

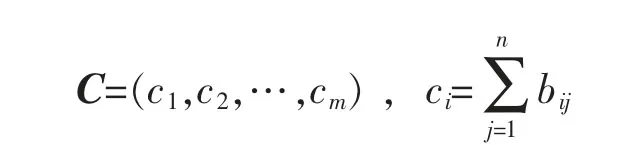
项的支持度按如下方式计算，构造m 维向量T＝（1，1，…，1），项目Ij的支持度按式（2）计算：

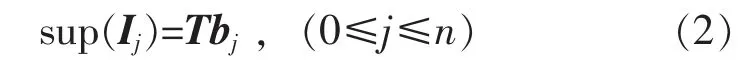
项目集 I1，I2，…，Ik的支持度按式（3）计算：

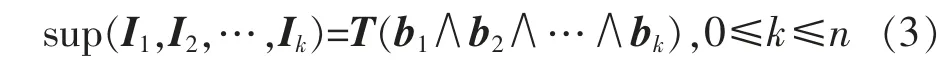
式中：∧表示逻辑与，如果支持度不小于最小支持度，那么该项集为频繁集。

2.2 算法描述

综上所述，算法的具体过程描述如下：

1）通过扫描数据库得到一项集的集合I，生成数据事务项的矩阵A以及计数矩阵B，并用向量C记录数据集中各事务项的规模。

2）候选集 C1＝I，根据式（2）计算各项支持度，剔除小于最小支持度的项而获得频繁集L1。

3）令项集大小k＝1，根据数据集事务项规模的情况确定分段支持度计算的分段数s。

4）分段计算频繁k项集Lk在数据事务规模为p∈[k，q]（q＝k+s-1）的支持度，将计数矩阵 B 按事务项规模划分为s个分段计数矩阵 ｛Bk，Bk+1，…，Bq-1，Bq｝，划分方式如下：扫描计数矩阵B和事务规模向量 C，如果 j＝ci（0≤i≤m，k≤j≤q-1），将 bi存入矩阵Bj中，否则将 bi存入矩阵 Bq中。

5）对各分段矩阵根据其维数构造向量Tj（k≤j≤q），对于频繁集 Lk中的每一项，由式（3）分别计算其在各分段矩阵中的支持度，得到各频繁集的多段支持度（Sk，Sk+1，…，Sq-1，Sq）。

6）由频繁集Lk按如下方式连接产生候选集Ck+1：令

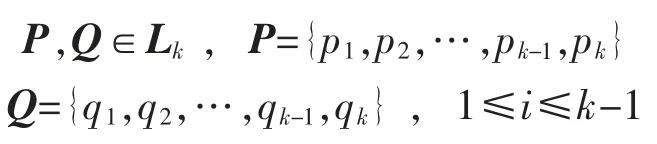
时 pi＝qi，而 i＝k时 pk≠qk，并且

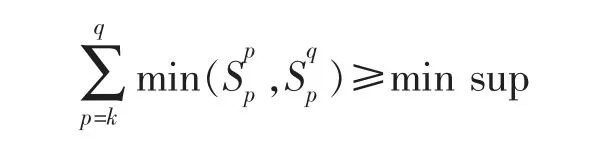
则可连接为｛p1，p2，…，pk-1，pk，qk｝。

7）根据性质2）剔除数据事务项矩阵A以及计数矩阵B中事务规模小于（k+1）的数据项，即 ci＜k+1的项。

8）由式（2）计算各候选集在剔除数据项之后的计数矩阵 B中的支持度，如果 sup（Ck+1）＜min sup，根据性质3）剔除此候选集，最后生成频繁集Lk+1。

9）如果 Lk+1≠Φ，令k＝k+1，转步骤 4）。

10）根据所有找到的频繁集生成满足最小置信度阈值的关联规则。

3 实例分析

给定事务数据库如表1所示，最小支持度min sup＝2，首先扫描数据库得到计数矩阵B和数据项规模记录向量C以及一项集I：

构造13维向量 T＝（1，1，…，1），则项目1的支持度为sup（1）＝Tb1＝7，同理其他项集支持度分别为（2，4，4，8，1，4，3，4），与最小支持度比较得到频繁集L1＝｛1，2，3，4，5，7，8，9｝。

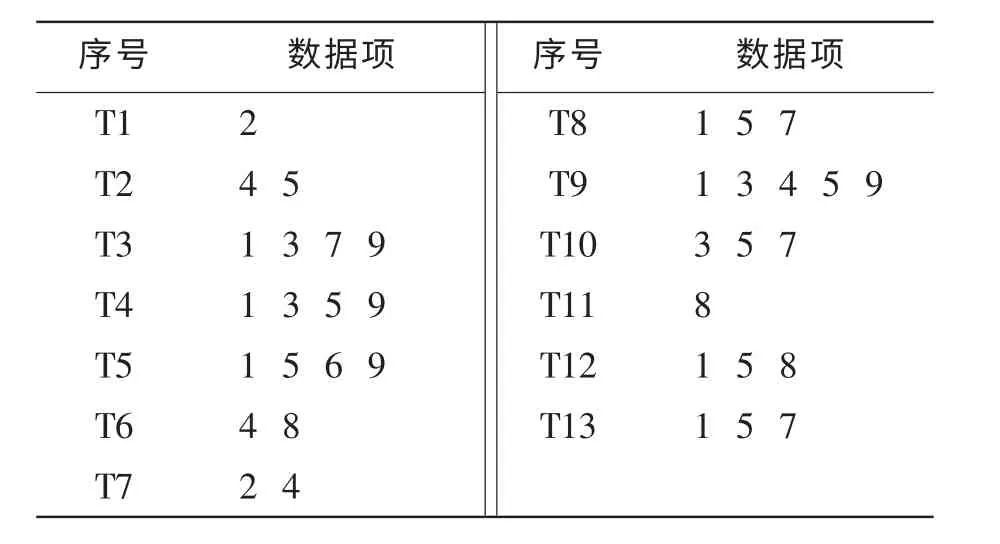
表1 事务数据库

取分段支持度计算的分段数s＝4，将矩阵B 按数据项规模 c＝｛1，2，3，≥4｝划分为4个分段矩阵：

并构造向量

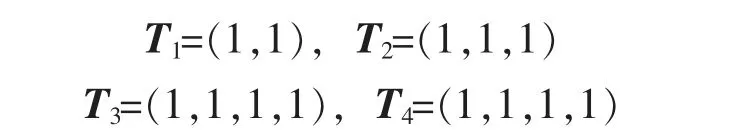
则项目1的分段支持度为

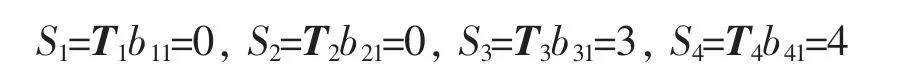
其他项的分段支持度计算同理，得到频繁项分段支持度如表2所示。

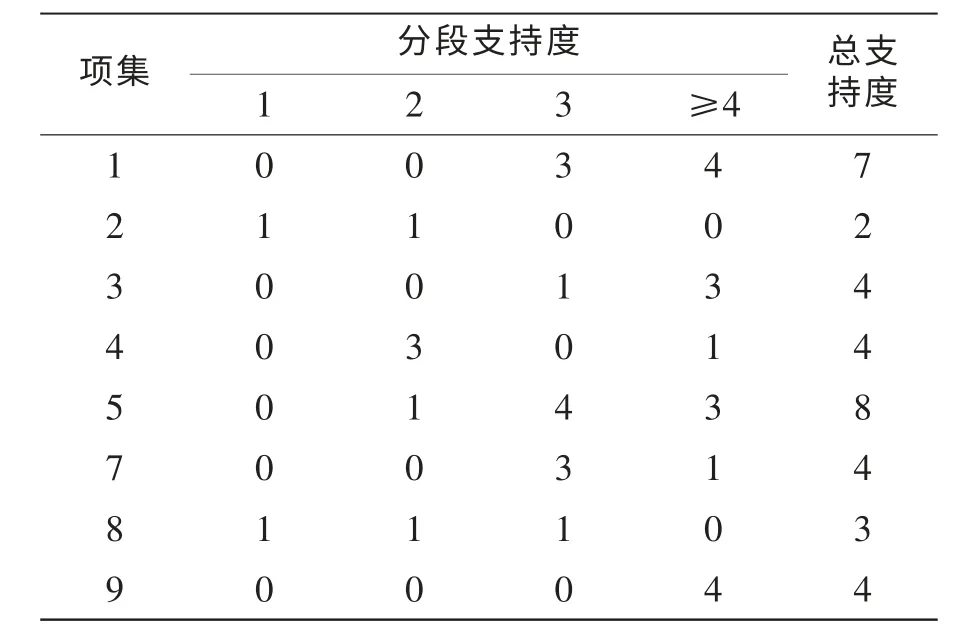
表2 频繁集L1 分段支持度

由性质3）可知项集2不可扩展，不可能继续生成频繁集，将其剔除，其余连接产生候选集C2，如

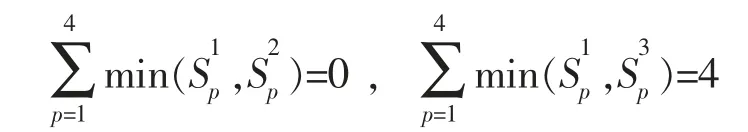
则可由项1和3 连接产生13，而不能由1和2 连接产生12，同理经过连接运算后产生的候选集C2：

C2＝｛13，15，17，19，35，37，39，45，57，58，59｝按式（3）计算候选集中各项支持度，如

其余各项同理计算，得到各项支持度为（3，6，3，4，3，2，3，2，3，1，3），剔除小于支持度阈值的项 58，得到频繁集L2：

L2＝｛13，15，17，19，35，37，39，45，57，59｝

剔除矩阵中ci小于2的行生成新的计数矩阵B，重复上述过程，产生新的候选集和频繁集，直到找不到更高一级的为止，计算结果如表3～4所示。

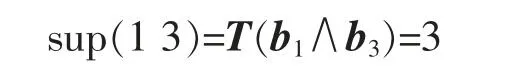
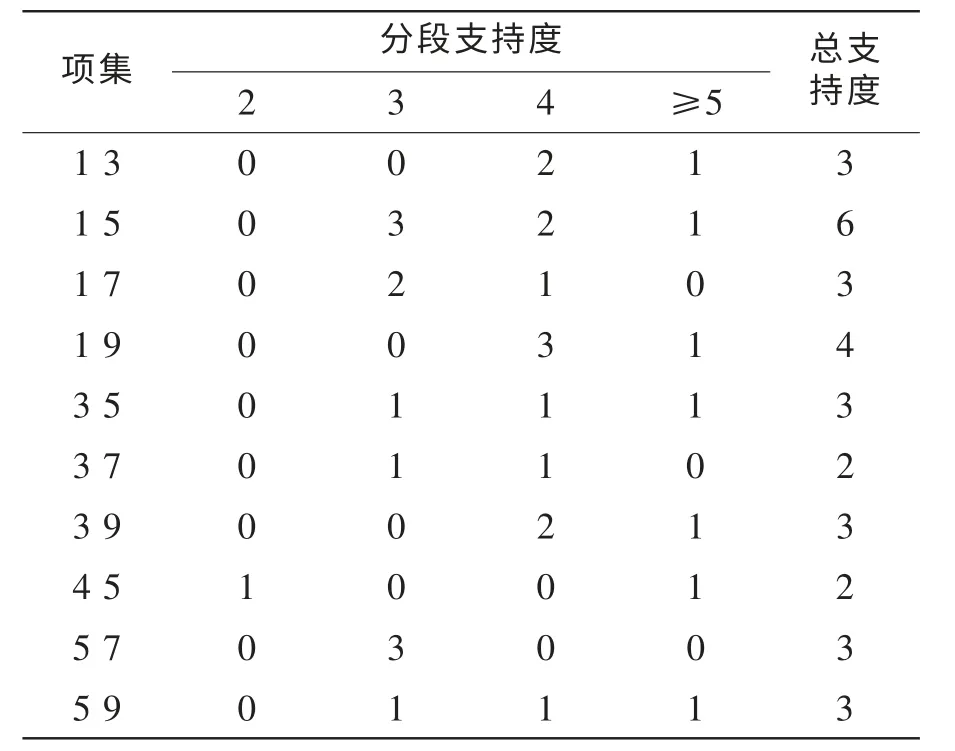
表3 频繁集L2 分段支持度

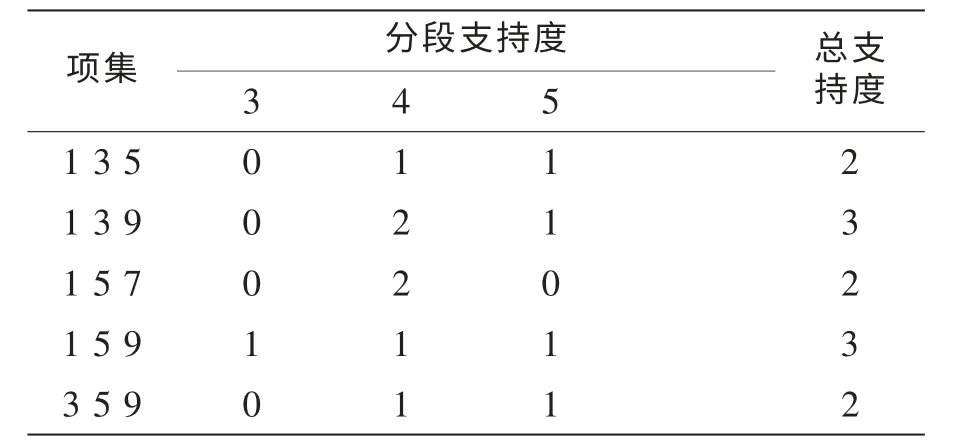
表4 频繁集L3 分段支持度

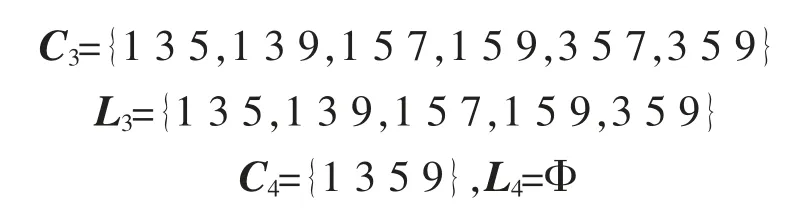
将本文算法的结果与Apriori算法比较，如表5所示。从比较结果可知，本算法具有以下特点：只需扫描数据库一次，能大幅度减少候选集的产生，支持度直接由矩阵快速计算，能比较高效地找出频繁集。

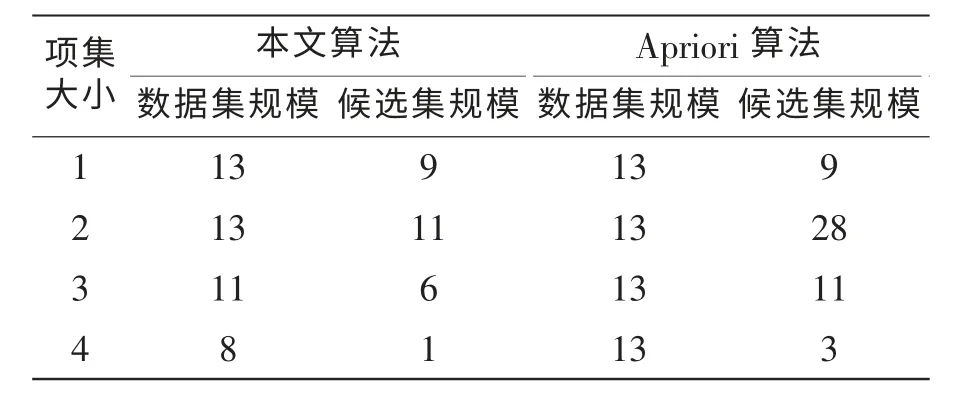
表5 算法运行效率比较

4 算法复杂度分析及实验仿真

4.1 算法复杂度分析

算法复杂度包括时间复杂度和空间复杂度，本算法采用矩阵计算的方式，只进行一次数据库扫描，初始化矩阵后数据库即不再使用，避免了耗时的I/O操作，并且采用支持度分段计算，在算法运行过程中不断剔除多余项集，矩阵规模和所需存储空间逐步减小，运算数据量很快减小，运行速度逐渐加快。

4.2 实验及结果分析

本算法对大型事务数据库的关联规则挖掘优势更加明显，算法运行过程中能对支持度方便和快速地进行运算，迅速缩减矩阵规模，能显著地提高寻找频繁集的效率。为测试本文算法的效率，选取了UCI机器学习数据集中4个有代表性的数据集，数据集规模和属性数如表6所示。

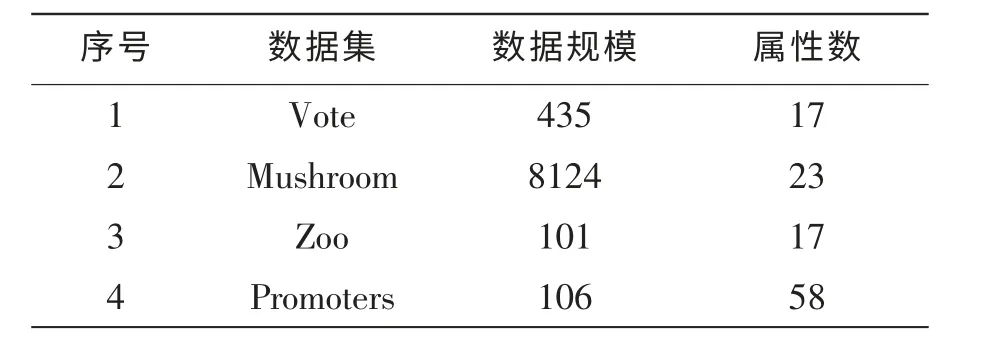
表6 测试数据集

算法以Matlab7.0 实现，利用其计时功能记录各算法的运行时间，最小支持度取值从0.2～0.5，将本文算法（MLIG）分别与多段支持度关联规则LIG算法[1-2]、基于矩阵的Apriori算法（MApriori）[2]和FPGrowth算法[5]进行比较，实验结果如图1所示。

从实验结果可以看出，本文中提出的算法运行效率有了比较大的提高，超出了比较高效的FPGrowth算法，尤其在给定的支持度阈值较小的情况下，Apriori算法和MApriori算法需要产生大量候选集，FP-Growth算法需要进行复杂的操作产生FP-Tree，算法过程需要庞大的存储空间，而本文算法避免了这些耗时的运算，运行时间大幅度减少，随着最小支持度阈值的提高，候选集的生成量减少，各算法运行时间均有所缩短，而本文算法运行时间仍然是最短的，因此在大型事务数据库的关联规则挖掘上更有优势。

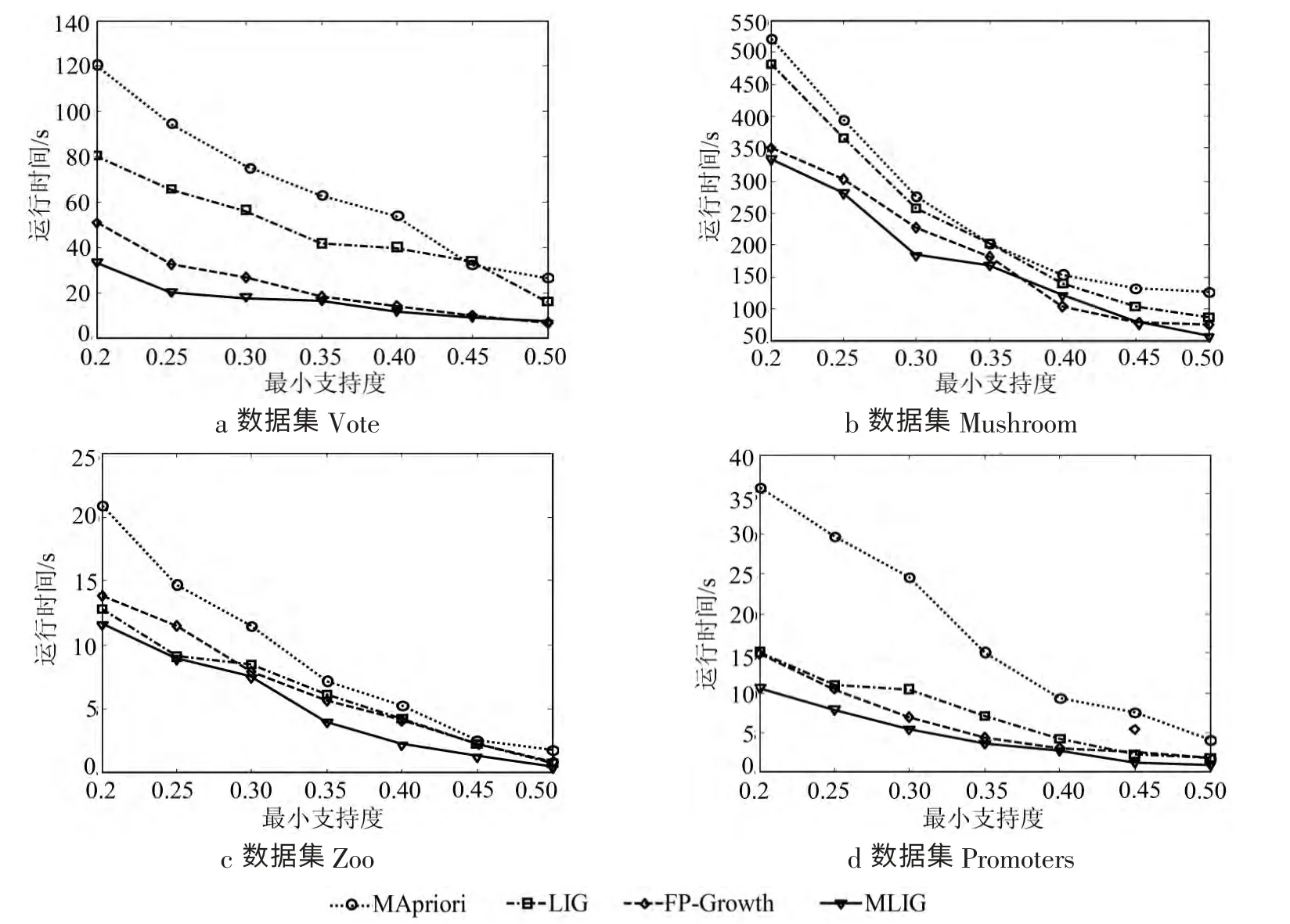
图1 各算法对不同数据集的执行时间对比图

5 小结

本文算法建立在矩阵计算的基础上，支持度的计算均在矩阵中完成，避免了频繁扫描数据库所造成的时间开销，同时将分段计算项集支持度的思想应用其中，充分利用其性质及时舍弃不可能生成频繁集的候选项，在较大规模事务数据库上能显著地缩小候选集规模，提高频繁集寻找速度，与经典Apriori算法以及一些改进算法相比，能快速地进行关联规则的挖掘，进一步增加了其实际应用价值。

[1]李雄飞，等.多段支持度数据挖掘算法研究[J].计算机学报，2001，24（6）：661－665.

[2]吴绍函，余昭平.基于矩阵的关联规则挖掘算法[J].计算机工程，2008，（34）23：31－33.

[3]Bonchi F，Lucchese C.Pushing tougher constraints in frequent pattern mining[C]//Ho T B，Cheung D，Liu H.LNCS 3518：PAKDD.Heidelberg：Springer，2005：114－124.

[4]Enrique L，Federico B，Antonio F C.Towards Personalized recommendation by two－step modified apriori data mining algorithm[J].Expert System with Application，2008，35（3）：1422－1429.

[5]赵洪英，蔡乐才，李先杰.关联规则挖掘的Apriori算法综述[J].四川理工学院学报：自然科学版，2011，24（1）：66－70.

[6]Tan Pang－Ning，Michael Sreinbach，Vipin Kumar.Introduction to data mining[M].Posts ＆ Telecom Press，2006：246－273.

[7]岳海涛，李杰，肖琳琳.基于位置索引矩阵的关联规则挖掘算法[J].计算机工程，2010（36）22：61－63.

[8]何建忠，吕振俊.基于两个矩阵的关联规则挖掘优化算法[J].计算机工程，2008，34（17）：56－58.

[9]Liu H T，Guo R X，Jang H.Research and improvement of Apriori algorithm of association rule mining[J].Computer applications and software.2009，26（1）：146－149.

[10]王娟勤，李书琴.基于矩阵的关联规则挖掘算法研究与改进[J].计算机测量与控制，2011，19（9）：2275－2278.

[11]Cui Guanxun，Li Liang，Wang Keke，Gou Guanglei，Zou Hang.Research and improvement of Apriori algorithm of association rule mining[J].Computer applications.2010，30（11），2952－2955.

[12]Yin Qun，Wang LiZhen，Tian QiMing.A weighted association rules mining algorithm based on probability[J].Computer Application，2005，25（4）：805－807.

[13]吕桃霞，刘培玉.一种基于矩阵的强关联规则生成算法[J].计算机应用研究，2011，28（4）：1301－1303.

[14]李超，余昭平.基于矩阵的Apriori算法改进[J].计算机工程，2006，32（23）：68-69.

[15]倪志伟，高雅卓，李伟东，束建华.基于矩阵的增量式关联规则挖掘算法[J].计算机工程与应用，2008，44（13）：153-155.