基于飞思卡尔32位Kinetis－K60单片机的直立行驶智能车设计

杨正才，吕科，朱乐

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

0 引言

智能车控制技术已成为一项新兴技术，它涉及汽车、电子、自动化控制、传感技术、信号处理、多个学科的知识领域[1]。作为一门新兴技术，此技术为汽车主/被动安全、无人驾驶技术等领域的研究提供了必要的技术保障。

直立行驶自平衡智能车在国外应用非常广泛，能够在自动循迹仓储物流、执勤巡逻、基地训练等方面作为中、短距离代步工具。从美国的Segway 再到中国日江公司的ChegCar，两轮直立自平衡智能车正逐步走进人们的日常生活，但是由于价格和安全性等诸多问题，普及应用还需要一定的时间。

笔者以电动小车为研究对象，搭建了一个基于32位Kinetis－K60 单片机的智能车控制系统，系统框图如图1所示，通过两侧的固定线性CCD 传感器动态摄取路面图像，识别白色跑道两侧的黑色引导线。该控制系统在路面信息识别、小车转向和速度的设定和偏差纠正、小车对黑色引导线的追踪等方面，提出了较为理想的解决方案。

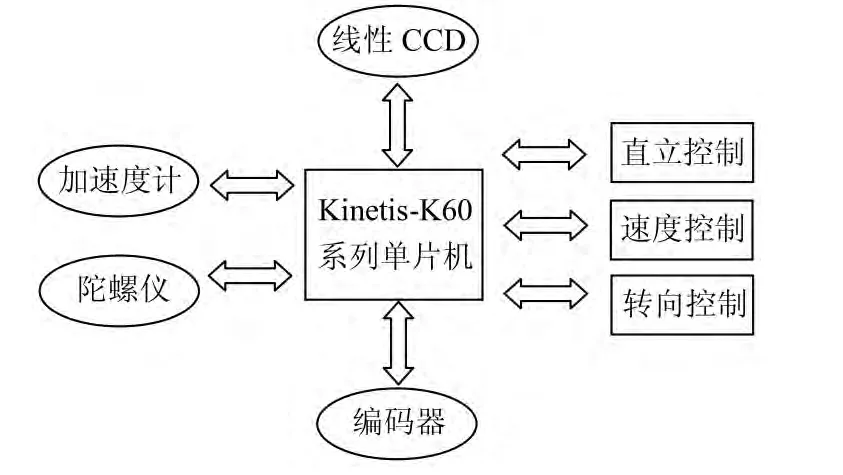
图1 系统功能框图

1 系统总体方案的设计

智能车系统采用飞思卡尔的32位控制器Kinetis－K60 单片机作为核心控制处理器，Kinetis是基于ARM CortexTM－M4 内核的具有超强可扩展性的低功耗、混合信号微控制器，具备高实时性等特点[2]。智能车的路径识别信号由线性 CCD 传感器采集，经ECU的A/D模块处理后，用于小车的运动控制决策，由ECU 发出PWM 波，驱动电机对智能车进行加速和减速控制，以及两电机的差速转向控制，使小车在赛道上能够自动识别引导线，以稳定的姿态向前行驶。

2 智能车机构调整与优化

为了保证直立智能小车的稳定性，应当尽可能地降低小车的重心，然后要进行2套传动机构的匹配及循迹传感器的稳定。最终方案所做优化如下：

1）线性CCD 传感器安装在小车中部，由于高度下降，采集的宽度减小，因此改为2个线性CCD，对称安装在小车的两侧。为了方便调节小车的前瞻，安装线性CCD的塑料支架有2个互相垂直的活动轴，支架又是由2个螺钉固定，在安装支架时只固定一个，另一个在车身上的滑槽中滑动，这样就形成了3个互相垂直的自由旋转轴，保证了在调节前瞻时，2个线性CCD的扫描区域基本在一条直线上，并且与赛道两侧的黑线垂直。调节好合适的角度后，用热熔胶固定3个旋转轴，方便今后随时更改角度，也起到了固定的作用。

2）供电电池安装在车身下部，可以极大地降低小车的重心，但同时也会使小车平衡时呈一定的倾斜角度，此时若直接将加速度计的电路板平行贴在车身上，则不能充分利用加速度计的灵敏区域，且车体向两侧倾斜时测得的偏角，会出现一侧偏大、另一侧偏小的情况。因此，加速度计的电路板是以一定的倾斜角度安装在车身上，使小车平衡时加速度计的测量值尽量靠近灵敏度最高的区域[3]。

3）小车驱动电机的选择，会影响到小车的整体性能。在相同情况下，选择高功率的电机可以达到更高的速度，但对电机的控制精度会下降，调节难度增大；而选择低功率的电机可以对电机控制更精确，小车更稳定且调节相对简单，但是牺牲了小车的最高速度。不管选择的哪一种，都要尽量保证两侧电机的性能相近，否则会对控制的稳定性造成不必要的困难。本系统选用RS－380SH型号的直流伺服电机。

3 智能车硬件电路设计

3.1 电源模块

电源模块对于一个控制系统来说极其重要，关系到整个系统是否能够正常工作，因此在设计控制系统时应选好合适的电源模块。本系统使用标准车模通用7.2 V 2000 mAh Ni－cd 电池供电，单片机控制器、路径识别的CCD 传感器、陀螺仪和加速度传感器均使用3.3 V工作电压[3]。编码器需要 5 V 电源。因篇幅所限，具体电源硬件设计内容不再赘述。

3.2 电机驱动模块

为提高伺服电机响应速度，直立行驶智能车的伺服电机工作电压可采用7.2 V 供电。故直流电机使用7.2 V 2000 mAh Ni－cd 电池直接供电。图2为电机控制原理图。

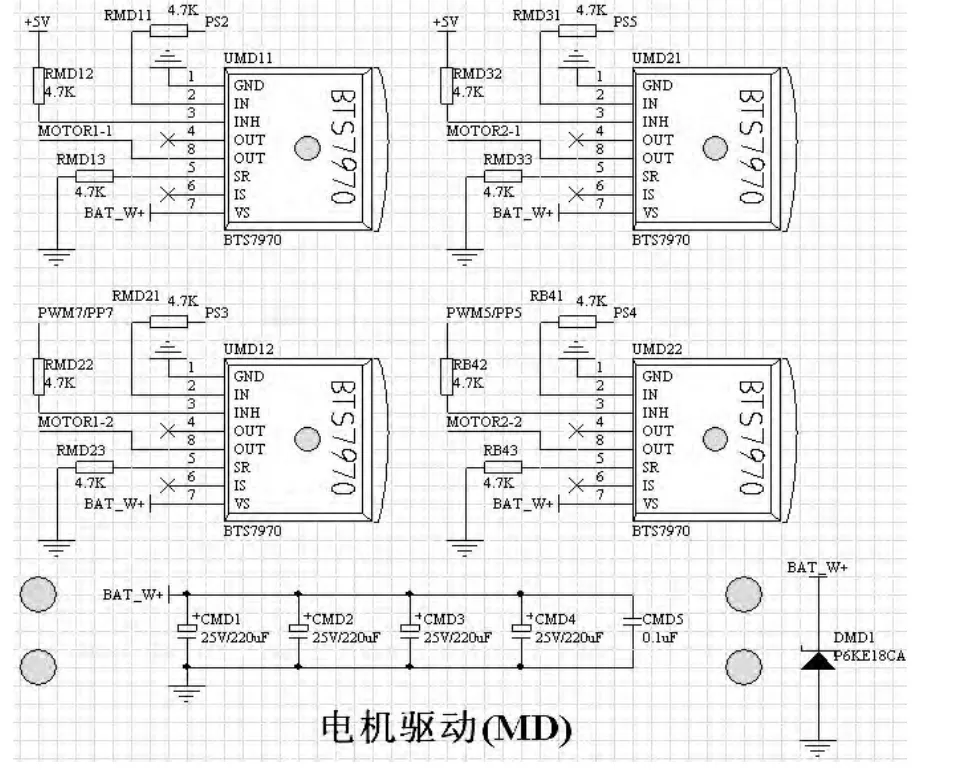
图2 电机驱动电路原理图

电机驱动方案采用4个BTS7970 构成2个全桥电路，分别控制2个电机正反转。

3.3 角度传感器电路

角度传感器电路主要是将陀螺仪信号进行放大滤波。由于加速度传感器采用低g值的传感器MMA7260，它的输出信号很大，不需要再进行放大。角度传感器电路所包含的陀螺仪电路和加速度计电路如图3所示。

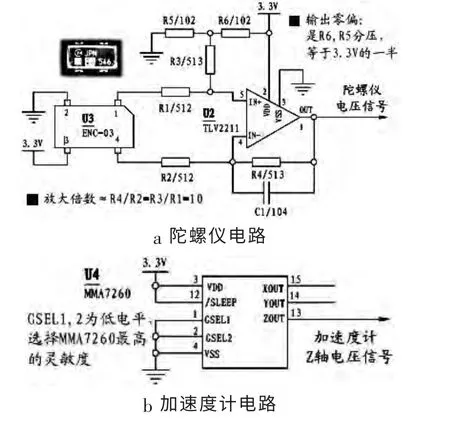
图3 角度传感器所含电路

3.4 路径检测传感器

TSL1401CL线性传感器阵列由一个128×1的光电二极管阵列、相关的电荷放大电路以及内部的像素数据保持模块组成，它集成了起始和停止时间的所有像素。该阵列128个像素，其中每一个具有光敏面积3524.3平方微米。像素之间的间隔是8微米。操作简化内部控制逻辑，只需要一个串行输入端（SI）的信号和时钟CLK，如图4所示。

图4 线性CCD 功能框图

3.5 光电编码器

光电编码器是一种旋转式位置传感器，在现代伺服系统中广泛应用于角位移或角速率的测量，它的转轴通常与被测旋转轴连接，随被测轴一起转动。可将被测轴的角位移转换成一串脉冲量[5]。

光电编码器分为绝对式和增量式2种类型。增量式光电编码器具有结构简单、体积小、价格低、响应速度快、性能稳定等优点，应用更为广泛。在高分辨率和大量程角速率/位移测量系统中，增量式光电编码器更加具有优越性[5]。绝对式编码器能直接给出对应于每个转角的数字信息，便于计算机处理，但当进给数大于1 转时，须作特别处理，而且必须用减速齿轮将2个以上的编码器连接起来，组成多级检测装置，使其结构复杂、成本高。

本系统使用的是欧姆龙E6A2－CW3C 编码器，如图5所示。此编码器为200线的增量式编码器，每旋转一圈生成200个脉冲，通过检测一定时间内的脉冲数，经过换算就可以算出小车的即时速度。

图5 光电编码器

4 智能车软件设计

4.1 智能车的直立控制

直立行走的小车就相当于倒立的单摆，它之所以无法像一般的单摆一样自己恢复到平衡位置，是因为倒立摆的回复力与偏转方向同向，不仅不会使倒立摆回到平衡位置，反而会越来越偏离平衡位置，因此，要使倒立摆保持平衡，必须施加一个与偏转方向相反的外力[6]。结合小车可能的运动方向，只能通过小车前后加速行驶产生的加速度来对抗使其倾斜的趋势。

要产生合适的加速度，首先通过陀螺仪采集小车绕车轴的角速度，加速度计采集垂直于车身的加速度，经过换算统一单位之后，让角速度积分逼近加速度计算出的角度与角速度通过互补滤波算法融合，这个角度即为此次计算节点相对于上次计算节点的角度变化量，通过PD 运算即可作为控制电机的PWM值，使电机以合适的转速运转，达到控制小车平衡的要求，其原理如图6所示。

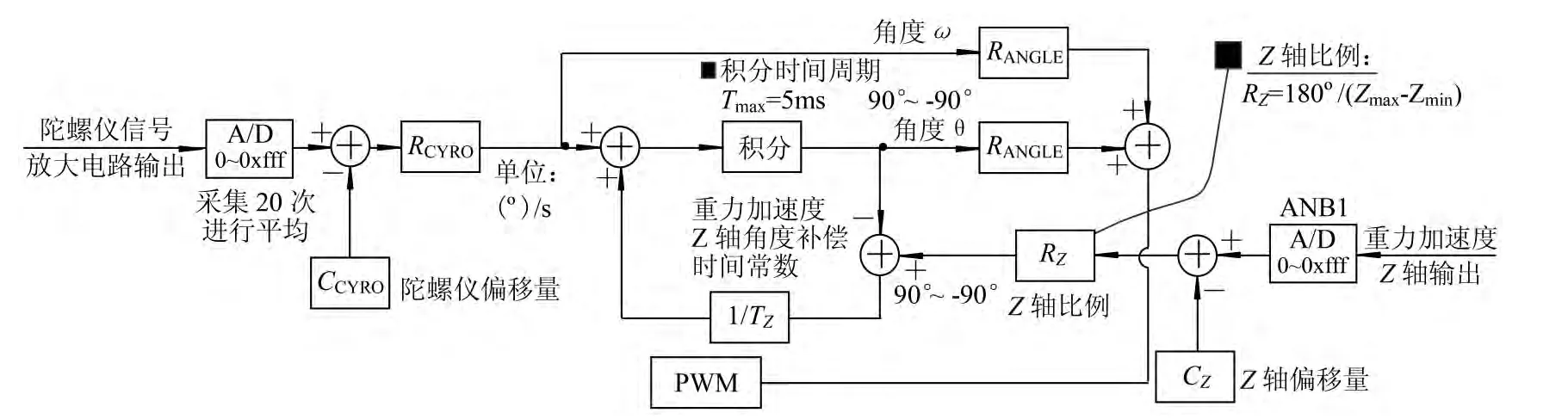
图6 直立控制算法

4.2 线性CCD 传感器的路径识别

在智能车的两侧分别安装一个线性CCD，寻找两边的黑线，中间空出5cm 左右空间，如图7所示。

图7 线性CCD 传感器排布方案

传感器在赛道上可能需要判断的状态有很多种，如普通赛道、起跑线处、十字交叉线处等，如图8～9所示。识别出智能车处于何种路况，便于给出不同的控制策略。

图8 普通赛道

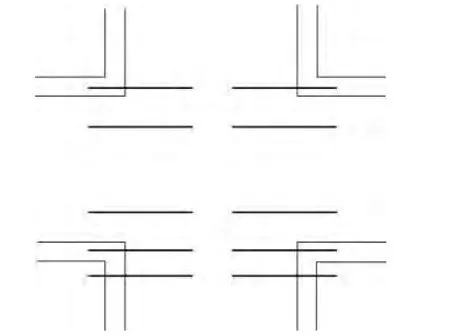
图9 十字交叉线处

4.3 智能车转向控制

根据小车偏离中心位置的程度给小车分配不同大小的转向值，基本思想是偏离程度越大给小车的转向值越大，这样可以保证在严重偏离赛道中心的情况下给小车最大的转向值以保证小车快速回到中心位置，在算法上采用的是PD 控制：

转向 PWM值＝Kpe（t）+Kd[e（t）-2e（t-1）+ e（t-2）]

单纯的PD 控制在小车处于低速状态时效果还可以，随着速度的提高，小车在转向时的角速度也要相应提高，在面对连续的变向转向时，由于惯性作用，转向时间存在严重的延迟现象，导致小车冲出赛道。为了解决这个问题，系统同时测量了绕赛道平面法线旋转的角速度，同样用PD算法算出一个增益量来抵消由于惯性带来的转向延迟[7]。通过不断调节PD值的大小并观察现象，取得合适的PD值后，比较完美地解决了转向延迟的问题。

4.4 智能车速度控制

利用单片机上的脉冲捕捉端口捕捉车速传感器在单位时间内的脉冲得出当前车速，采用PI 闭环控制，根据实际中的不同负载状况及快速调整PWM 波使电机及时调整转矩，最终使车稳定于预定的目标速度；同时为了避免速度控制对直立控制的干扰，在测量电机转速时取10个主循环周期之和，PI 控制的输出量也除以10，分10次输出，增量式PID计算公式为

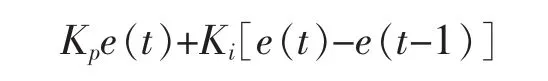
在普通赛道上，PI 控制已足够满足要求，但是在通过10°左右的坡道时，单纯的PI 控制无法使小车产生足够的加速度，而下坡时有无法及时减速，这不利于快速顺利地完成比赛。为了解决这个问题，在小车上坡时提高了加速度计的零偏值，使其有向前倾斜的趋势，而下坡时降低加速度计的零偏值，使其有向后倾斜的趋势，从而产生足够的加速度进行加速和减速。

除此之外，在普通赛道上时，也对小车的速度偏差进行了限制，超过限制则提高或减小加速度计的零偏值，使其向相应方向倾斜，产生一个额外的加速度。

5 系统测试

为了验证直立自平衡智能车的运行状况，以图10所示的智能车为测试对象，进行了包括机械性能、偏转角度、速度控制性能等方面的测试。

图10 直立中的小车

5.1 角度测量测试

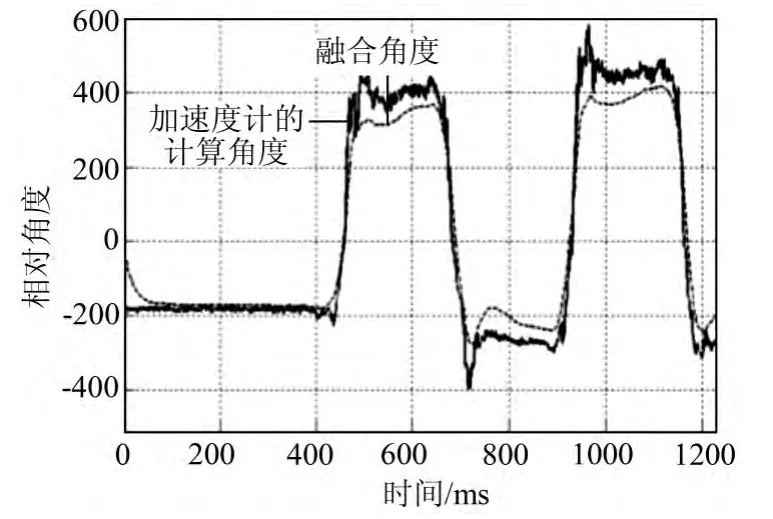
图11 融合角度计算验证

为了使直立小车能稳定行驶，直立控制必须可靠，而直立控制首先要求能正确计算出偏离的角度。在验证角度计算的正确性时，由于动态的准确角度无法获取，因此系统测试采用的是静态测量，即每次手动晃动小车到一定角度，停留一定时间，再反向晃动到另一个角度，反复多次，然后将通过加速度计算出的角度与融合算法算出的角度进行对比。由于加速度计在系统没有太多的振动时测量结果比较准确，因此可以对比加速度信号计算出的角度与融合算法算出的角度，观察其变化速度及静止时的值是否相似。用Matlab软件仿真计算出的特性曲线图，如图11所示，可以看出，融合角度和加速度计计算角度的最大值都在数值400附近（此数值为陀螺仪与加速度信号数据融合后的角度值，即调试量，无量纲），表示车身相对平衡位置的倾角都在30°左右，而正常情况下，车身的摆动幅度也在此范围，所以测试时只摆动到这个角度。经实验发现，两者吻合较好，证明该系统角度计算较准确，实时性较高。

5.2 速度控制测试

速度控制的测试工作可以通过单片机实时存储一段速度信息，然后通过串口发送回电脑，用Matlab软件作图直接观察[8]。低速时的速度控制相对于高速更加稳定，小车以目标速度为1 m·s－1的低速运行进行测试。速度控制验证曲线如图12所示，稳定后速度基本在目标范围内小幅度波动，目标跟踪性很好。

6 结论

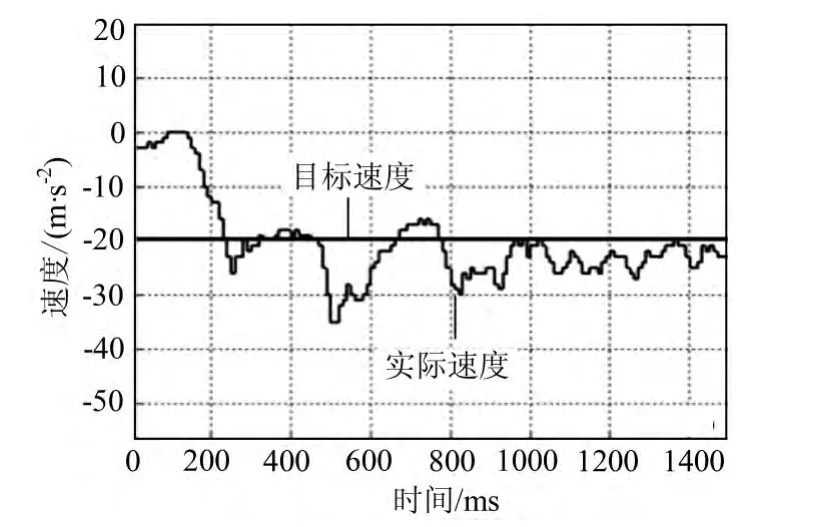
图12 速度控制验证

该直立自平衡智能车在硬件上采用2个线性CCD 传感器同时循迹，范围大、周期短。较好地解决了丢失黑色引导线的问题；直立控制算法可以控制小车顺利通过路障、坡道等特殊道路情形，稳定性较高。经过多次实际测试，可以在赛道上稳定、可靠的行驶，抗干扰性强，并可自主优化路径。

1）在整体结构上，对各个部件机械结构进行了重组优化，降低了重心，为小车的稳定运行提供了极大的便利。

2）直立控制采用的互补融合滤波，经过不断调试，已经能适应各种赛道；循迹算法中采用了面阵CCD的部分滤波算法，同时结合线性CCD的特点进行相应信号融合，配合滤光片的使用，系统对光线的适应性得到了很大的提高，进一步提高了系统的稳定性。

[1]张启秋，蔡雄友.两轮自平衡智能小车控制系统的设计与实现[J].五邑大学学报：自然科学版，2013：4－11.

[2]王宜怀，刘晓升.嵌入式应用技术基础教程[M].北京：清华大学出版社，2005：155－171.

[3]卓晴，黄开胜，邵贝贝.学做智能车[M].北京：北京航空出版社，2007.

[4]孙同景.Freescale 9S12 十六位单片机原理及嵌入式开发技术[M].北京：机械工业出版社，2008.

[5]姜桥.电子技术基础[M].北京：人民邮电出版社.2009.

[6]庞立江，孟立辉.对赛格威电动车的改进探讨[J].石家庄理工职业学院学报，2009（1）：46－52.

[7]吴广鑫.坐式两轮自平衡车的系统研究[D].哈尔滨：哈尔滨工程大学，2011.

[8]刘金琨.先进 PID控制及MATLAB 仿真[M].北京：电子工业出版社，2004.