舰船通信网络结构复杂性实证分析❋
梅 丹 王公宝 胡伟文 张建军
(海军工程大学应用数学系 武汉 430033)
1 引言
舰船通信网络是为保障作战指挥、武器控制、协同动作、后方勤务、警报和情报报知、装备保障等信息的传输与交换而建立的网络体系,是信息系统的重要组成部分[1]。舰船通信网络日趋呈现复杂性的特点,对其进行研究是否可以采取复杂网络的研究思路呢?由此而生成的网络结构模型是否符合复杂网络的基本特征?复杂性特征对现实舰船通信系统建设又有何帮助?本文针对上述问题,从复杂网络角度出发,用邻接矩阵表示某舰船通信网络拓扑模型,并仿真计算了该网络的平均路径长度、聚类系数等统计特性指标,验证了该通信网络的小世界特性。该结论为将复杂网络的研究成果运用到未来军事系统建设中提供了积极的理论启示和参考价值。
2 复杂网络理论
2.1 复杂系统网络模型
现实世界中大多数复杂系统可以用网络模型来描述,例如规则网络和随机网络[2]。规则网络所能描述的系统范围极其有限;随机网络的随机性十分符合真实网络中连接的某些特性,但是对动态演化系统所表示出来的一些特性却无法予以说明。1998年,Watts和Strogatz通过以某个很小的概率p切断规则网络中原始的边,并随机选择新的节点重新连接,构造出一种介于规则网络和随机网络之间的小世界网络[3]。小世界网络是复杂网络的一种重要模型。此外,复杂网络模型还包括无标度网络、局部演化网络等。关于复杂网络更为详细的描述参见文献[4]。
2.2 复杂网络的特征参数
对于一个无向无权网络G=(V,E),其中V表示节点的集合,E表示边的集合。经典复杂网络理论中定义了以下四个重要参数[5]来描述网络特性:
1)平均路径长度L
在一个网络中,两个节点i、j间的最短距离dij定义为连接这两个节点的最短路径上的边数。对所有节点对的最短距离求平均值,就得到了该网络的平均路径长度:
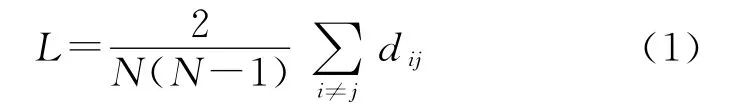
它是以边长作为长度单位进行度量的拓扑距离。路径长度的分布是所有节点对之间最短路径的统计分布特性。平均路径长度是网络的特征尺度,可以表征网络的连通性。
2)聚类系数C
复杂网络具有高度的集团性,网络的聚类系数C是专门用来衡量网络节点集聚程度的一个重要参数。在网络中,每个节点的聚类系数可表示为

式中,ai为连接节点i的三角形的个数,bi为连接节点i的三元组的个数。比较直观的定义方法为:假设节点i有ki个近邻节点,则ki个近邻节点之间至多存在ki(ki-1)/2条边,而ki个近邻节点之间实际存在ti条边,则节点i的聚类系数为

聚类系数表征了近邻节点联系的紧密程度,进一步对所有节点的聚类系数求均值就可以得到网络的聚类系数:

3)度数及度分布
节点i的度定义为与该节点连接的其他节点的数目,即与节点i关联的边的数目,记为ki。
网络中所有节点的度的平均值称为网络的平均度,记为〈k〉。对于一个边数为M,节点数为N的网络,其平均度数为〈k〉=2 M/N。
分析度分布的传统方法是直接画出顶点度数的直方图,这种方法的缺点是直方图的宽度平滑,会使得落入同一直方内的数据点的值间差异全部丧失。现在使用较多的考察复杂网络节点度分布的一个可行方法是采用累积分布函数法。这里,定义p(k)表示度数为k的节点个数n(k)占节点总数N的百分比,易知度数概率分布具有完备性:

其中,kmin和kmax分别表示网络中节点度数的最小值和最大值。同时定义节点度数累积分布函数(Cumulative Degree Distribution Function)Pc(k),用P(k≥K)表示度不小于K的节点的概率分布,常数K∈[kmin,kmax],则节点度数的累积概率就可以表示为

根据随机网络理论,复杂网络的度分布服从二项分布或大N极限下的泊松分布,其特征是网络中绝大多数节点的度值分布在均值附近,在此意义下,复杂网络是均质网络。
4)介数及介数分布
Holme和Kim在研究网络演化所导致的过负荷时,假设网络中任意两节点之间信息或能量的交换都通过最短路径进行,选择用介向中心性(Betweennes Centrality)来评估网络中的节点和边的网络流量[6~8],其后介向中心性也被简单地称为介数(betweenness)。节点v的介数B(v)和边e的介数B(e)表达式类似,可分别定义为
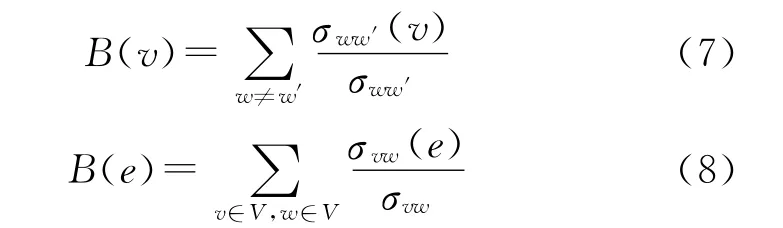
式中,对于w≠w′且w,w′≠v的所有节点对,σww′为节点w、w′之间的最短路径数目,σww′(v)为 w、w′之间经过v的最短路径数目;σvw(e)为节点v、w之间包含边e的最短路径数目,σvw为节点v、w之间的最短路径数目。
定义节点(边)介数累积分布函数(Cumulative Betweenness Distribution Function)为 Pc(B),用P(B≥B′)表示介数不小于B′的节点(边)的概率分布,Bmax表示网络中节点(边)介数的最大值,常数B′∈[Bmin,Bmax],节点(边)介数的累积概率就可表示为
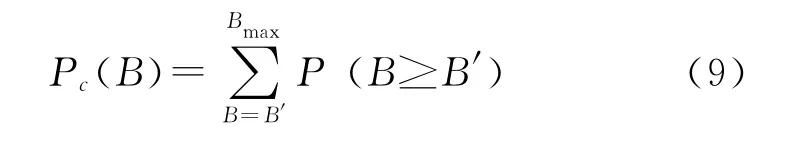
3 舰船通信网络结构及其拓扑模型
采用复杂网络理论研究舰船通信系统特性,要将通信网络简化为拓扑模型。在这里,各个通信实体简化为节点;由于通信实体之间存在信息的传输与交换,连线代表两个通信实体之间有直接的通信联系。图1为某舰船通信网络拓扑结构图,出于保密要求,该图为经过适当处理后的部分拓扑结构图。
为了方便计算机进行处理,用邻接矩阵A对网络拓扑模型进行表示,A中元素aij规定为:aij=1,当节点i与j相邻;aij=0,当节点i与j不相邻。

图1 某舰船通信网络拓扑结构图(部分)
4 舰船通信网络复杂性分析
在Watts和Strogatz关于复杂网络的小世界现象的研究,以及Barabasi和Albert关于复杂网络的无标度特性的工作之后,人们对不同领域的大量实际网络的拓扑特性进行了广泛的实证性研究,得到了各个领域、各种实际网络的各项基本统计数据[9]。如社会领域中电子邮件网络的平均路径长度L=2.0,聚类系数C=0.16;信息领域 WWW(nd.edu)网络的平均路径长度L=2.4,聚类系数C=0.29。这两种网络具有类似于规则网络的较高聚类系数和类似于随机网络的较小平均路径长度,即小世界特性。
由式(1)和式(2)可以计算出某舰船通信网络的平均路径长度L=2.4318和聚类系数C=0.1934。通过与电子邮件网络和信息领域网络的平均路径长度值和聚类系数值进行比较,发现某舰船信息化网络的统计数据与上述两种网络的数据接近。进一步验证了某舰船通信网络也具有小世界特性。可以看到,某舰船通信网络具有较短的平均路径长度,说明网络中信息的流动比较顺利。这也使得军事网络为各作战单元提供迅速、准确、有效的通信支撑。
通过计算,上述某舰船通信网络节点的度分布如图2所示。在这里,节点的度即为通信实体直接进行信息交换的通信实体数目。
由图2可见,第14号节点的度为4,在整个网络中最大。这意味着该节点与其他节点的联系比较紧密,十分重要。也就是说该节点受到攻击或者损害会造成网络的级联故障,甚至造成整个网络的瘫痪[10]。通信节点的重要性还可以从介数指标上得到验证。如图3所示,14号节点的介数最大。节点的介数值越高,说明该节点的影响力越大,地位也越重要。

图2 某舰船通信网络节点度分布

图3 某舰船通信网络节点介数
5 结语
本文首先介绍了复杂网络理论,重点阐述了复杂网络的四个度量参数:平均路径长度、聚类系数、度数、介数;然后将某舰船通信网络的拓扑结构进行了抽象表示,并用邻接矩阵表示了各通信实体之间的通信联络关系;最后通过仿真计算了该通信网的各项基本参数。计算结果表明,某舰船通信网络具有复杂网络的小世界特性。复杂网络提供了一种全新的视角,帮助我们从整体上把握军事通信网络的复杂性,更好地认识其拓扑结构及相应的动力学特征。
[1]李德毅,王新政,胡刚锋.网络化战争与复杂网络[J].中国军事科学,2006,19(3):111-119.
[2]Erdos P,Renyi A L.On the evolution of random graphs.Publ[J].Math.Inst.Hung.Acad.Sci.,1960,5:17-60.
[3]Watts D J,Strogatz S H.Collective dynamics of‘small-world’networks[J].Nature,1998,393(6684):440-442.
[4]Albert R,Barabasi A L.Statistical mechanics of complex networks[J].Review of Modern Physics,2002,74(1):47-97.
[5]汪小帆.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
[6]Holme P.Edge overload breakdown in evolving networks[J].Physical Review E,2002,66(2):036119.
[7]Holme P,Kim B J.Vertex breakdown in evolving networks[J].Physical Review E,2002,65(1):066109.
[8]Holme P,Kim B J,et al.Attack vulnerability of complex networks[J].Physical Review E,2002,65(1):056109.
[9]Newman M E J.The structure and Function of Com-plex Networks[J].SIAM Review,2003(45):167-256.
[10]Crucitti P,Latora V,Marchiori M.Model for cascading failures in complex networks[J].Physics Review E,2004(69):045104.

