基于二维高斯样条函数的水下重力被动定位❋

王志刚 顾雪峰

（1.91550部队 大连 116023）（2.海军工程大学兵器工程系 武汉 430033）（3.海军工程大学兵器科研部 武汉 430033）

1 引言

目前，对于水下潜器的被动定位是导航、定位领域研究的一个热点和难点问题。水下潜器的惯导系统（Inertial Navigation System，INS）误差随时间积累，因此必须要通过其它导航方式实时或定期修正INS。出于隐蔽性要求，水下潜器又很难利用卫星或无线电信息，此时利用水下地理特征信息的辅助导航定位就是很好的选择。常用的辅助导航定位系统有地形、重力辅助导航系统［1～2］等，目前这些辅助导航系统都是以各种匹配算法为核心来获得潜器的最佳匹配位置（真实位置），以实现对惯导系统的修正。传统的匹配算法主要分为单点迭代和序列迭代两类，分别以SITAN［3～4］（Sandia Inertial Terrain－Aided Navigation）和ICCP［5～6］（Interval Closest Contour Point）算法为典型代表。这些匹配算法分别在实时性和稳定性方面有其优点，但是为了保证良好的匹配效果对潜器的运动规律和初始误差环境有很多严格的限制［7］，因而也限制了其应用范围。针对这一问题，本文提出一种直接利用观测重力进行水下被动定位的新模式，应用该方法的前提就是确定重力异常与潜器位置（大地经、纬度坐标）的精确解析表达式，之后与航空领域的目标被动定位原理相似，由于观测重力中包含了目标的位置坐标信息，直接通过非线性滤波算法，就可对潜器的航行位置进行最优估计。

2 二维高斯样条函数逼近

直接利用地球重力进行定位，在很大程度上取决于观测重力与目标所在位置关系的确定，也就是地球重力场模型的确定。目前常用的各类全球重力场模型［8］无论在阶次和精度方面都已经达到了很高的水平，它本质上属于球坐标系下的调和分析，因而应用过程中需要计算大量的Legendre系数，使得模型计算量巨大，而这对于定位的实时性是一大考验，另外现有的大部分全球重力场模型非线性比较严重，也不太利于滤波估计时的线性化处理。

近年来，高斯样条函数在医学影像、数字地形构建、计算机图形学及地球物理等领域有较为广泛的应用，文献［8］讨论了一维高斯样条在协方差函数代数确定中的应用，文献［9］采用高斯函数作为样条基函数对计算区域重力异常进行二维整体逼近，文献［10］讨论了高斯样条函数逼近局部重力异常的相关影响因素。采用高斯样条函数逼近局部重力异常运算简单且最终解析式是统一的，文章在该样条逼近函数的基础上建立了重力量测方程并结合具体的目标运动状态方程，成功运用扩展Kalman滤波实现了对潜器位置的最优估计。

2.1 二维高斯样条函数逼近数学原理

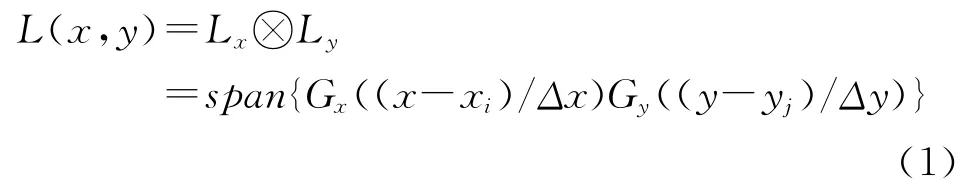
即有

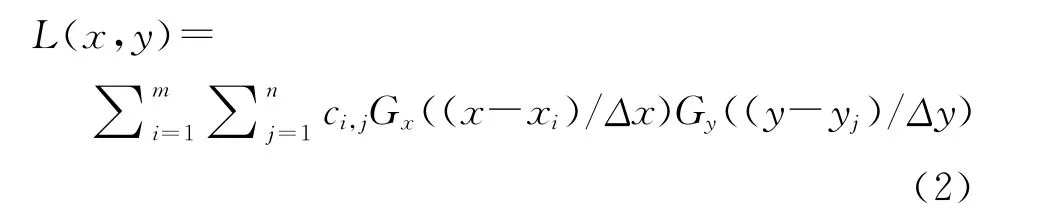
不妨设

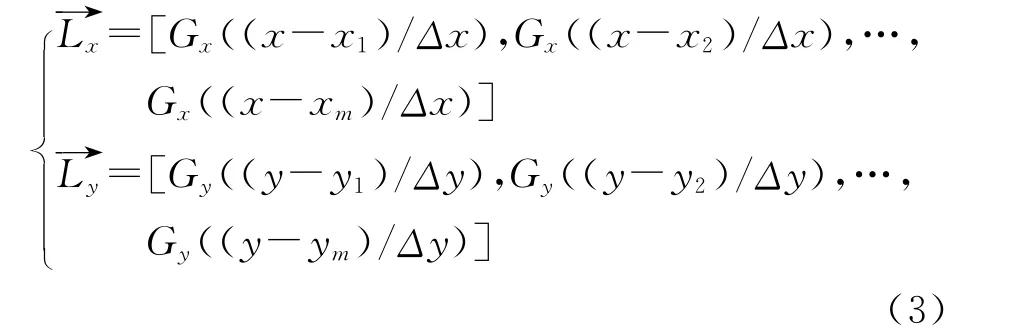
则上式可以简化为矩阵形式：

则根据插值条件｛L（xi，yj）＝zi，j｜i＝1，…，m；j＝1，…，n｝，有如下线性方程：

易知X、Y 均为非奇异矩阵，即式（5）有唯一解，解方程即得到系数矩阵C，将系数矩阵代入式（2）便得到该局部重力异常基准图二维高斯样条函数逼近解析式。

由式（5）可以看出系数矩阵C由X、Y与Z唯一确定，而X、Y由矩阵的阶数和ax，ay决定。文献［9］曾对求逆计算误差与和计算阶数的关系进行过详尽的探讨。经讨论可知：系数矩阵的求解过程中如X、Y矩阵阶数过高且ax、ay过小或阶数过低且ax、ay过大时，X、Y矩阵的求逆存在较大误差。而当X、Y矩阵阶数小于5或ax、ay值小于5时，矩阵求逆运算误差较小。考虑到求逆计算误差以及实际应用中用到的格网区域远大于5×5，我们即可采用文献［10］给出的斐波那契数列方法对ax∈［1，s］，ay∈［1，s］区间内进行寻优。

2.2 二维高斯样条函数逼近精度分析

取范围i为117°E～121°E，j为21°N～25°N，分辨率为2′×2′的卫星测高反演重力异常数据作为已知重力异常基准图。文章在该已知2′×2′重力异常基准图的基础上，取4′×4′格网点处重力异常数据作为基础数据点，进行二维高斯样条函数逼近，获得该范围局部重力异常基准图解析表达式，并据此计算分辨率为2′×2′的重力异常逼近值，然后与已知的2′×2′格网处重力异常值进行比对分析。

最终的仿真结果如图1所示，其中图1（a）为已知2′×2′重力异常基准图，图1（b）为由4′×4′重力异常基准图逼近的2′×2′重力异常基准图，由此可以看出二维高斯样条函数逼近的局部重力异常基准图解析式能较好地描述这一范围的重力异常基准图。

图1（c）、图1（d）分别为逼近误差图及相应的误差统计图，表1为误差统计表，由图1、表1可以得出，试算区域4′×4′格网点处二维高斯逼近计算值绝对误差均值为0.19mGal且99.5%计算点绝对误差小于1mGal，逼近精度可以满足导航定位要求。鉴于重力二维高斯样条逼近函数的连续形式、与经纬度坐标具有明确的解析关系以及自身的高精度，使得这一逼近函数十分适合用于重力被动定位时所需的量测方程。

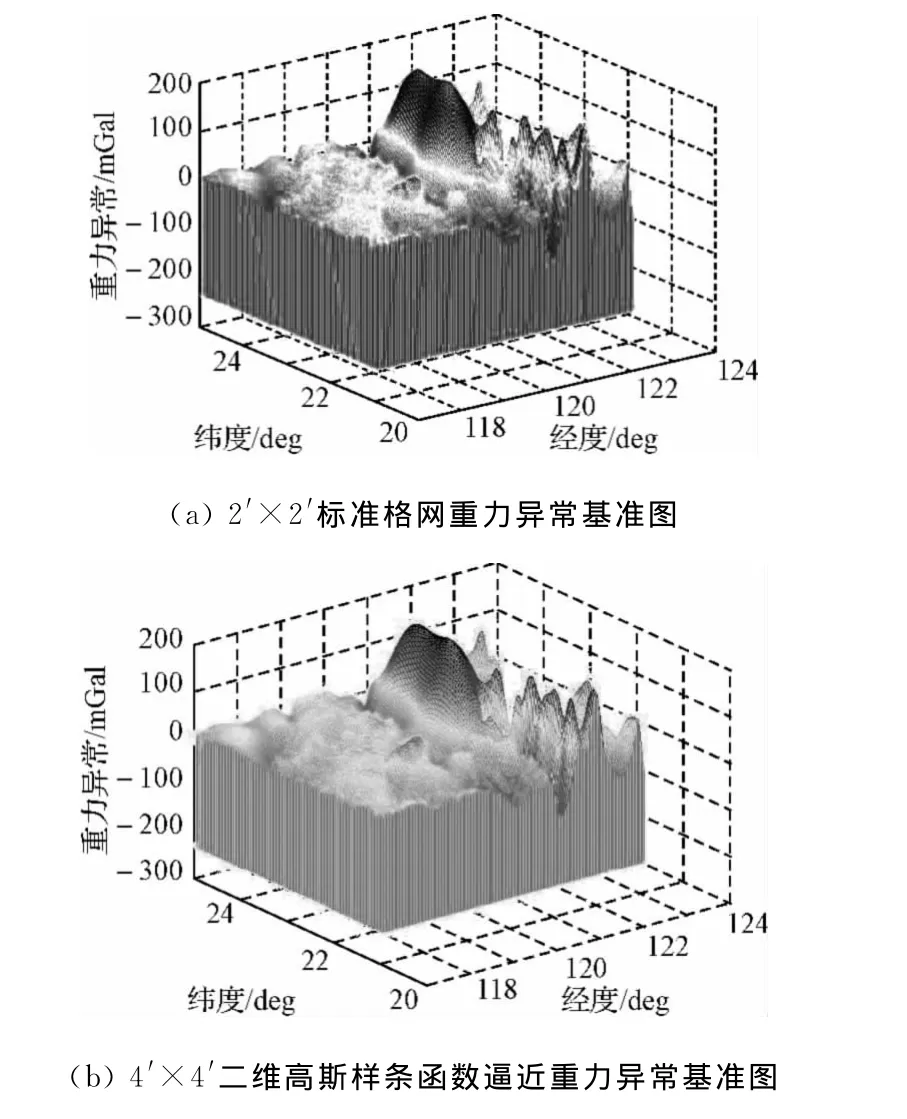
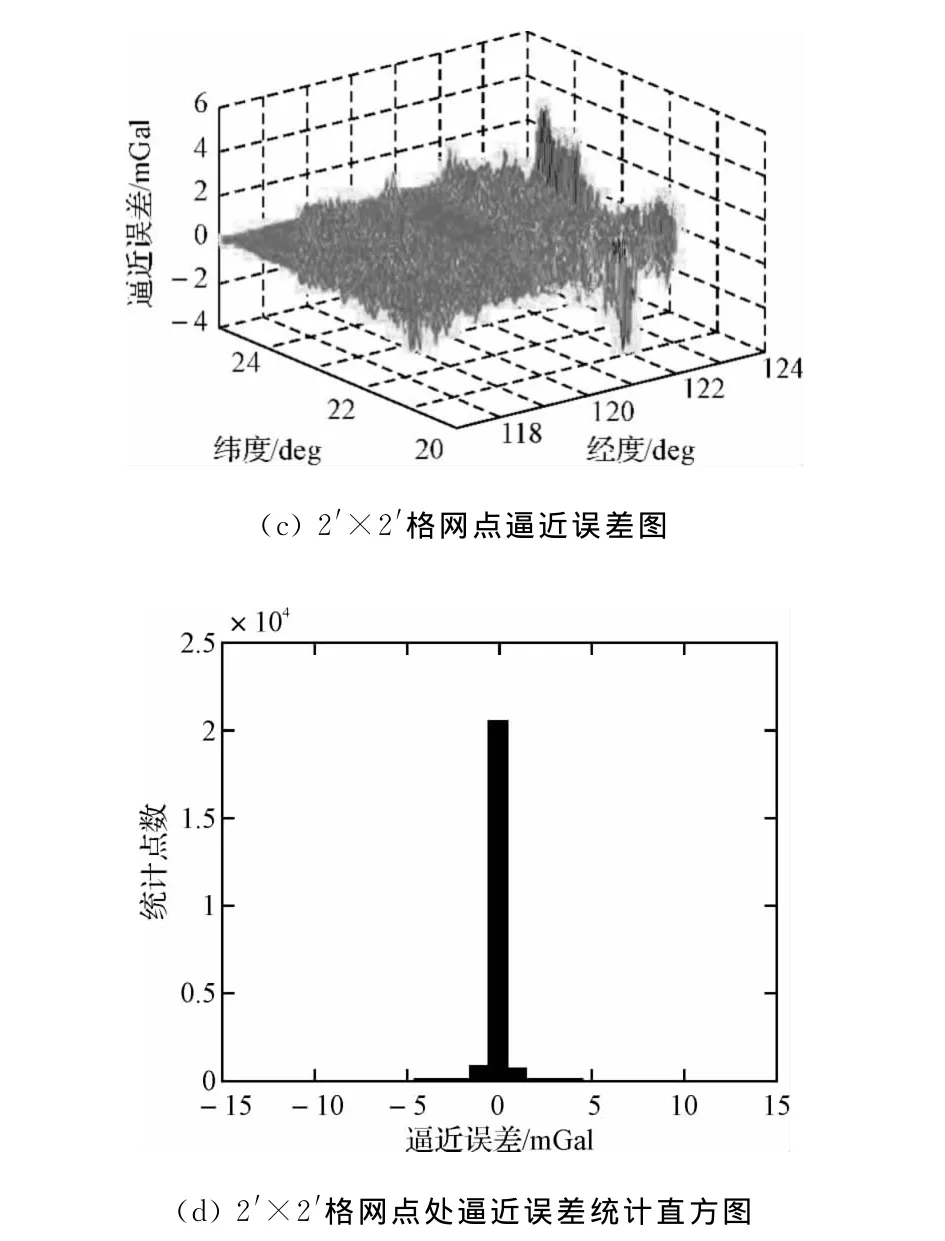
图1 局部重力异常基准图二维高斯逼近仿真实验

表1 计算值和真值比较（单位：mGal）

3 水下被动定位模型的建立

水下被动定位较水面与航空领域的被动定位难度更大，究其原因就是在强调隐蔽性的前提下水下可利用的观测量更少，即便有可用的观测量其解析形式也十分复杂，因而当今潜器的水下定位、导航多是基于特定的地理信息数字图，通过采用各种匹配算法和观测信息在数字图上估算出潜器的位置坐标，这类方法的核心就是匹配算法，但是匹配算法在应用时为了保证具有好的定位效果，对潜器的初始误差、运动模式具有诸多限制，且有的匹配算法还不能保证定位的实时性（如ICCP算法），能保证实时性的又容易出现误匹配（如Sitan算法）。水面和航空领域的被动定位相对简单，它只需要建立合适的目标运动状态方程再由具体的观测方程，将真实观测量中所包含的我们感兴趣的目标状态（如经、纬度坐标）通过非线性滤波技术［11～14］估算出来。

建立潜器状态方程如下：

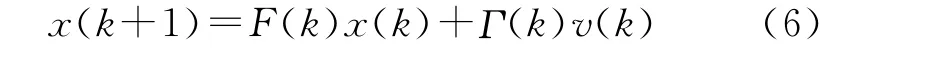
其中

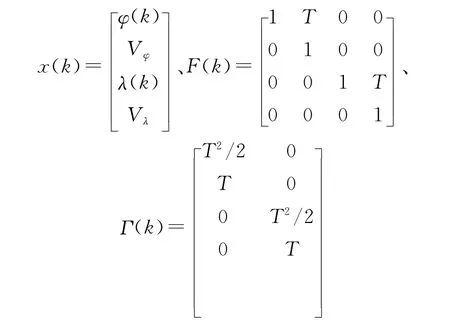
其中F（k）、Γ（k）为k时刻的状态和扰动矩阵，φ（k）和λ（k）为k时刻的潜器经纬度坐标，Vφ、Vλ为潜器在纬度和经度方向上的运动速度，T为采样间隔，v（k）为零均值过程白噪声。在目标定位领域这一建模方式包含了目标所有的匀速和匀加速运动情况。

对于水下潜器定位的观测值取为重力仪观测重力

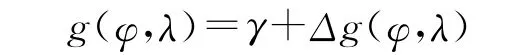
其中γ＝9.780325（1＋0.00530244sin2（φ）－0.00000587sin2（2φ））为 WGS84椭球正常重力公式。

设

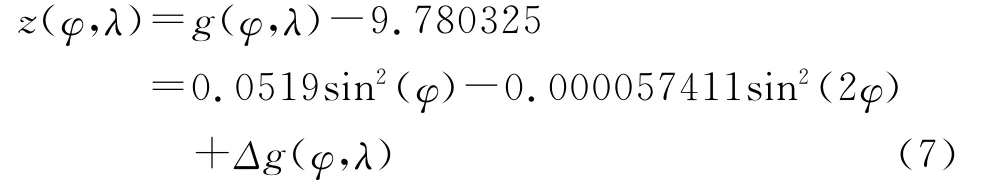
其中

z（φ，λ）为水下定位时将要采用的量测值，式（7）就是本文最终建立的量测方程。

式（7）与经、纬度坐标是一种非线性关系，本文在对潜器位置误差进行最优估计时采用的是经典的扩展卡尔曼滤波（EKF），因而需要对式（7）进行泰勒展开的线性变换。

将式（7）分别对φ、λ求导可得

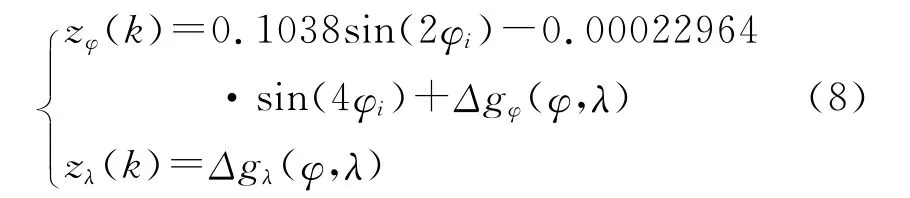
其中

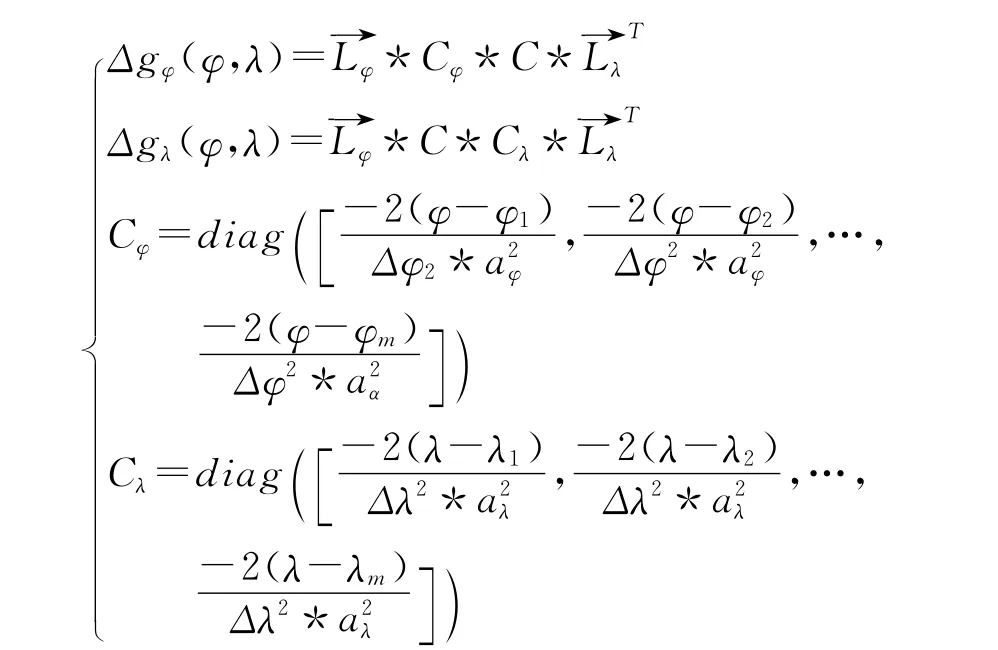
对式（7）进行泰勒展开并舍去泰勒展开高阶项，并直接给出线性化后的量测方程如下

其中H（k）为线性化后的量测矩阵，W（k）为观测噪声。

由状态方程（6）及线性化后的量测方程（9）通过非线性滤波算法就可对目标的水下位置进行最优估计。

4 仿真分析

以2.2节给出的区域范围，i为117°E～121°E，j为21°N～25°N，分辨率为2′×2′的卫星测高重力异常数据作为已知重力基准图进行仿真分析。水下潜器初始位置为（21.5°，121.7°），北向和东向航速分别为 9nmile／h 和 －5nmile／h，加速度都为1nmile／h2，整个仿真阶段取为100个采样点，采样间隔为6min，总航行时间为10h；重力仪测量数据的仿真采用重力异常数据加入测量噪声的方法。现今海洋重力仪的动态精度已经达到1mGal量级（如L＆R的S型海洋重力仪），因此重力测量误差一般取方差为1mGal2的白噪声，另外，考虑到各种数据滤波及误差综合影响（如交叉耦合、厄特沃什改正），取一项白噪声作为滤波估计的误差噪声，这个综合值根据经验取为9mGal2。采用50次的蒙特卡罗仿真，结果如图2～图5所示。

表2 定位误差统计表（单位：海里）

图2、图3为基于重力观测值的水下被动定位示意图，由两图可以看出估计航迹在大部分的航行阶段都能较好地反映真实航迹，只是由于运动模式转换在航行转弯时有一定程度的波动，由以上分析可以得出结论：

图2 重力被动定位示意图

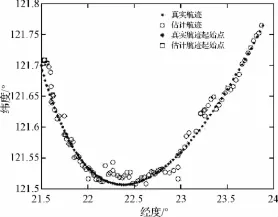
图3 定位放大示意图

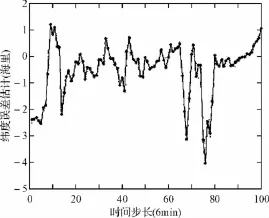
图4 纬度误差示意图

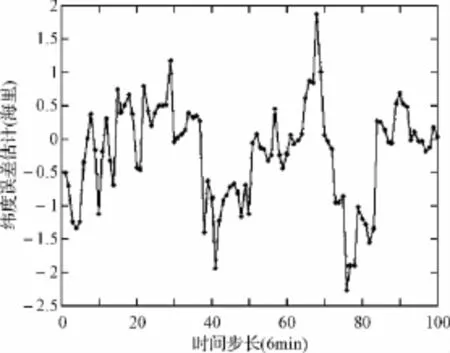
图5 经度误差示意图

1）以观测重力作为量测值是可以用来提取潜器位置坐标的，由图2、图3的被动定位示意图可以看出，估计航迹在大部分的航行阶段都能较好地反映真实航迹，这说明文章建立的量测方程是有效的，通过非线性滤波算法对量测值中的目标位置信息进行最优估计，可实现潜器的被动导航与定位。

2）图4、图5、表2给出的是本文重力被动定位方法的定位误差及统计结果，在10h的航行阶段最大纬度误差不超过4.02海里，平均纬度误差只有0.74海里，最大经度误差2.28海里，平均经度误差0.59海里，从以上数据及误差示意图可以得出结论，虽然经纬度误差存在一定程度上的波动，但总体的定位误差已经不随时间积累，这使得该定位模式在水下可长期使用。

5 结语

被动定位在军事领域具有极高的应用价值，文章将该原理引入潜器的水下被动定位，首先基于二维高斯样条函数逼近的重力场模型建立所需的量测方程，随后通过非线性滤波技术对水下潜器的位置坐标进行实时估计。该定位方法使用简单，无需使用传统的匹配算法，因而避免了匹配算法对潜器的初始环境以及惯导误差等的种种限制，最终的仿真结果证明，直接由实测重力数据对水下潜器进行定位是可行的，它的定位误差不随时间积累，另外随着海洋重力数据测量精度的不断提高，最终的定位精度也必将得到进一步的提高。

［1］Rice H，Mendelsohn L，Robert Aarons R，et al.Next generation marine precision navigation system［C］／／IEEE：Position Location and Navigation Symposium，2000：200－205.

［2］Moryl，J，Rice，H，Shinners，S.The Universal Gravity Module for Enhanced Submarine Navigation［C］／／IEEE Position Location and Navigation Symposium（PLANS'98）Record，20－23April 1998.

［3］Hollowell J.Heli／SITAN：a terrain referenced navigation algorithm for helicopters［C］／／IEEE Position，Location，and Navigation Symposium 1990（PLANS'90），Las Vegas，NV，USA，March 20－23，1990，616：625.

［4］许大欣.利用重力异常匹配技术实现潜艇导航［J］.地球物理学报，2005，48（4）：812－816.

［5］Behzad K.P，Behrooz K.P.Vehicle location on gravity maps［J］.Proceedings of SPIE－The International Society for Optical Engineering，1999：191.

［6］刘繁明，孙枫，成怡.基于ICCP算法及其推广的重力定位［J］.中国惯性技术学报，2004，12（5）：36－39.

［7］Bishop G.C.Gravitational field maps and navigational errors［J］.IEEE Journal of Oceanic Engineering，2002，27（3）：726－737.

［8］BIAN Shaofeng，JOACHIM M.determining the parameter of a covariance function by analytical rules［J］.ZfV，1999（7）：212－216.

［9］童余德，边少锋，蒋东方，等.基于高斯样条函数的局部重力异常场解析重构［J］.测绘学报，2012，41（5）：754－760.

［10］Overholt K J.Efficiency of the Fibonacci search method［J］.BIT，1973，13（1）：92－96.

［11］杨元喜.自适应动态导航定位［M］.北京：测绘出版社，2006.

［12］王丹力，张洪钺.惯导系统初始对准的非线性滤波算法［J］.中国惯性技术学报，1999，7（3）：17－21.

［13］吴俊伟，曾启明，聂莉娟.惯性导航系统的误差估计［J］.中国惯性技术学报，2002，10（6）：1－5.

［14］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，1998.