应用多抽头谱估计和小波变换的宽带频谱感知方法❋

朱永建

（海军驻苏州地区通信军事代表室 苏州 215101）

1 引言

当前静态频谱分配政策导致了频谱平均利用率低下的问题，认知无线电是一项有望解决该问题的智能无线通信技术。频谱感知［1］是认知无线电的一项关键技术，其目的在于寻找当前未被主用户占用的频谱空穴，供认知无线电使用，因此其需要在很宽频段内进行搜索，即宽带频谱感知。针对宽带频谱感知问题，目前研究人员已进行了大量研究，提出了一些频谱感知方法［2］。这些方法可以归纳为两种实现途径，一种是将感知频段划分成多个窄带，然后对各个窄带进行判决，这种方法感知时间过长。另一种途径是针对宽带采样后的信号，估计各个主用户信号子带的边界，从而得到频谱空穴。本文采用后一种途径，提出了一种应用多抽头谱估计和小波变换相结合的宽带频谱感知方法，仿真分析了该方法的性能。相对于周期图估计功率谱再利用小波变换的方法，本文方法具有更好的性能。

2 多抽头谱估计

周期图谱估计是一种常用的非参数功率谱估计方法，给定时间序列x（n），n＝0，1，…，N－1，周期图采用式（1）对功率谱进行估计：

为降低估计方差，还可采用如下平均周期图估计：

其中N／L为将x（n）顺序均匀划分的分段数，每段包含L个数据，段与段之间不重叠。

在实际中，周期图法可以用FFT实现，由于其实现简单，周期图法获得了广泛的应用。但是不可避免地存在缺陷，即无法解决估计偏差与方差的矛盾。那么，如何才能通过减少加窗引入的信息丢失来解决该矛盾？答案即为采用多个正交抽头（窗），即为 多 抽 头 谱 估 计 方 法［3］（multi－taper spectrum estimation，MTSE）的核心思想。多抽头谱估计使用的窗为Slepian序列，有时也被称为离散扁长球面小波函数［4］。Slepian序列的重要特征在于有限点数约束下它们的Fourier变换在带宽2W 内具有最大的能量集中度。这使得可以利用谱分辨率来交换谱特征，即可以在不增加估计偏差的情况下减少谱估计方差。换句话说，原有的偏差与方差的折中变成了偏差与分辨率的折中。因此，多抽头方法可以得到期望功率谱的准确估计。

令n表示离散时间，给定时间序列x（n），n＝0，1，…，N－1，MTSE估计采用式（3）：

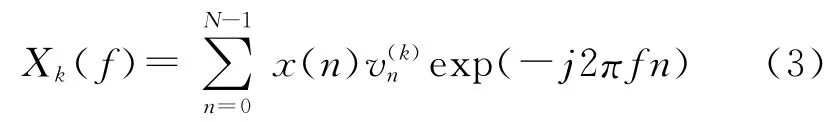
K为可控制多抽头谱估计方差的自由度。参数Co以及K的选择提供了谱分辨率、偏差、方差之间的折中。偏差在很大程度上由最大特征值ρ0（N，W）决定，其值由下式近似给定：

式（5）给出了总旁瓣能量。总旁瓣能量随着Co的增加快速减少。基于前几个具有最小旁瓣泄露的特征谱的谱估计由式（6）给定：

虽然低阶的特征谱具有很好的偏差性能，但是随着阶数K趋近于式（4）定义的极限值，特征谱的性能逐渐下降。文献［5］中采用一系列自适应权重｛dk（f）｝来降低高阶特征谱的影响。采用均方误差优化过程，得到如下权重公式：

其中，S（f）为真实功率谱，Bk（f）为第k个特征谱的宽带偏差，E［·］表示求均值，并且具有如下关系：

其中，σ2为方差：

为采用式（7）计算dk（f），需要知道真实功率谱S（f）。显然，如果知道真实功率谱，就不需要进行任何谱估计了。式（7）的作用在于可以建立一个迭代过程用来进行自适应谱估计：

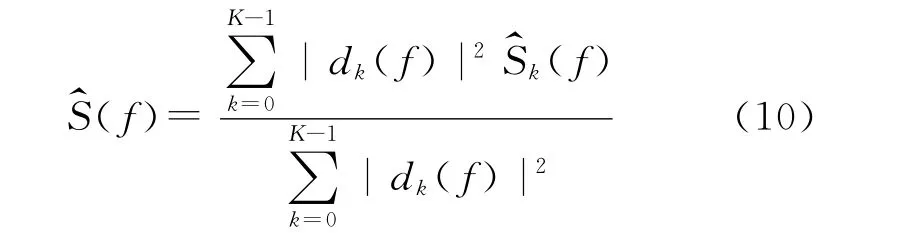
由此，可以得到如下递推式：

自适应谱估计得到的另一个有用参数是估计的稳定性度量，即：

3 宽带频谱感知方法

3.1 功率谱密度的小波变换

在频谱感知的应用中，小波变换［6］用来分析功率谱密度。令φ（f）表示具有m消失矩的紧支撑小波平滑函数，其m阶可微。φ（f）由尺度因子s扩展后为

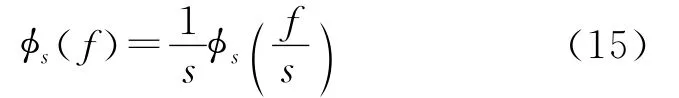
对于二进制尺度，s取2的指数次，即s＝2j，j＝1，2，…，J。令＊表示卷积运算，功率谱密度Sx（f）的连续小波变换为

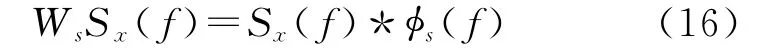
注意式（16）是针对功率谱Sx（f）进行计算的。从接收信号x（t）得到WsSx（f）有两种途径。一种是先计算x（t）的自相关函数Rx（τ）＝E｛x（t）x（t＋τ）｝，然后计算Rx（τ）的Fourier变换得到Sx（f），最后根据式（16）得到WsSx（f）。另一种途径则是先求φs（f）的Fourier反变换得到Φs（τ），并计算Rx（τ）＝E｛x（t）x（t＋τ）｝，然后求得Rx（τ）·Φs（τ），最后求Rx（τ）·Φs（τ）的Fourier变换得到WsSx（f）。

3.2 基于多抽头谱估计和小波变换的感知方法

宽带频谱感知最为关键的问题是如何估计得到各个子带的边界｛fn｝。PSDSx（f）在尺度s下的边界不规则点定义为WsSx（f）的局部剧烈变化点。函数的边界通常由其导数的形状表征。WsSx（f）的一阶导数为

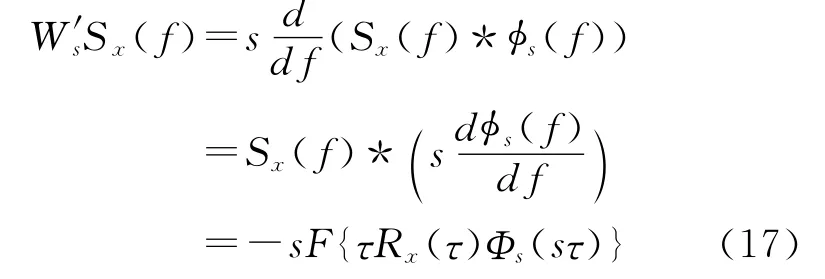
其中F｛·｝表示Fourier变换。一阶导数的局部极值点反映了待分析信号（功率谱）的不规则（畸变）特征［6～7］。因此，可以通过寻找一阶导数绝对值的局部极大值点来确定各个子带的频率边界［7］，即：

在边界突变剧烈的情况下，W′sSx（f）的局部极值点是能很好反映Sx（f）的突变特性，但是，当边界变换缓慢或受噪声影响严重的情况下，W′sSx（f）的局部极值点就不能很好地与Sx（f）的突变位置匹配，此时WsSx（f）的局部极值点更能反映Sx（f）的边界。因此，可以采用如下多尺度小波积［8］：

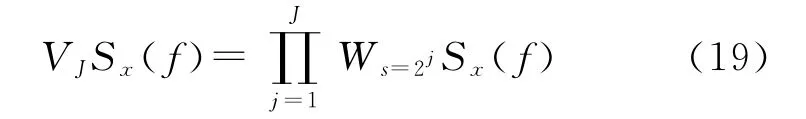
频率边界｛fn｝表现为｜VJSx（f）｜的局部极大值点。Sx（f）的各个子带边界通常具有不同的倾斜度，如果采用同一组尺度｛sj｝进行分析，则可能会漏掉一些边界。一种解决途径是采用多组尺度进行分析，然后再对各组尺度下估计所得的边界进行合并。

4 仿真分析

以下对本文方法性能进行仿真分析，仿真采用Haar小波，主用户信号为BPSK和QPSK信号，个数为3。图1给出了多尺度小波一阶导数积以及多尺度小波积的性能比较。其中图1（a）是周期图谱估计结果，图1（b）是多抽头谱估计结果，对比可知，多抽头谱估计更好地保持了功率谱子带边界的突变特性。图1（c）是针对多抽头谱估计进行小波变换的结果，图1（d）是最终找到的边界。由图可知多尺度小波积在第三组尺度下（s＝2j，j＝7，8，9，10）找到了各个子带的边界。

图1 多组尺度下小波（一阶导数）积

5 结语

宽带频谱感知是认知无线电的一项关键技术。本文在讨论多抽头谱估计和小波变换的基础上，给出了一种结合多抽头谱估计和小波变换的宽带频谱感知方法，利用了多尺度小波积。仿真结果表明在功率谱子带边界突变不是非常剧烈的情况下，该方法能够找到主用户信号频率边界，从而找到频谱空穴。

［1］S.Haykin.Cognitive radio：Brain－empowered wireless communications［J］.IEEE J.Sel.Areas Commun.，2005，23（2）：201－220.

［2］T.Yucek，H.Arslan.A survey of spectrum sensing algorithms for cognitive radio applications［J］.IEEE Communications Surveys ＆ Tutorials，2009，11（1）：116－130.

［3］S.Haykin，D.J.Thomson，J.H.Reed.Spectrum sensing for cognitive radio［J］.Proceedings of the IEEE，2009，97（5）：849－877.

［4］D.Slepian.Prolate spheroidal wave functions，Fourier analysis，and uncertainty v：The discrete case［J］.Bell Syst.Tech.J.，1989，57：1371－1429.

［5］D.J.Thomson.Spectrum estimation and harmonic analysis［C］／／Proc.IEEE，1982，70：1055－1096.

［6］S.Mallat，W.Hwang.Singularity detection ＆ processing with wavelets［J］.IEEE Trans.Info.Theory，1992，38：617－643.

［7］Z.Tian，G.B.Giannakis.A wavelet approach to wideband spectrum sensing for cognitive radios［J］.CrownCom，2006：1－5.

［8］E.P.L.de Almeida，P.H.P.de Carvalho，P.A.B.Cordeiro，et al.Experimental study of a waveletbased spectrum sensing technique［J］.IEEE Asilomar，2008：1552－1556.