一种粗糙集与DSmT融合故障诊断方法*
苏艳琴 张光轶 林 健
(1.海军航空工程学院研究生管理大队 烟台 264001)(2.海军航空工程学院科研部 烟台 264001)(3.91033部队 青岛 266071)
1 引言
装备的故障诊断是装备维修和综合保障中的重要环节,由于高新科技的不断渗入,装备的结构复杂性和使用要求的特殊性等,对装备的故障诊断也提出了新的更高要求。在电子装备的故障诊断中,由于故障部件间的相关性和相互作用,使得故障参数之间相互影响,出现了不确定、不一致和不完备的情况,如何解决不确定数据处理和不确定推理成为困扰装备保障人员的一个难题[1]。
粗糙集理论是一种处理不确定、不一致和不完备数据的理论,而证据理论对不确定性推理具有一定优势,因此开展二者融合是一种适宜的装备不确定故障诊断方法。相对于Dempster-Shafer(DS)证据理论,Dezert-Smarandache理论(DSmT)是在DST的基础上,于2002年由Dezert和Smarandache提出的DST的推广理论。DSmT不仅能很好地表示和处理不确定信息,而且可以很好地表示和处理冲突信息,其辨识框架中元素的要求也不再是相互排斥的。因此,用元素的交来表示并发故障,这就使得并发故障诊断有了理论框架。
2 相关理论
2.1 粗糙集理论
1982年,波兰数学家Z.Pawlak提出的粗糙集理论定义在上近似集和下近似集的基础上[2]。设U为有限个对象构成的集合(即论域),R为U上的等价关系,则称为Pawlak近似空间;对于任意X⊆U,称


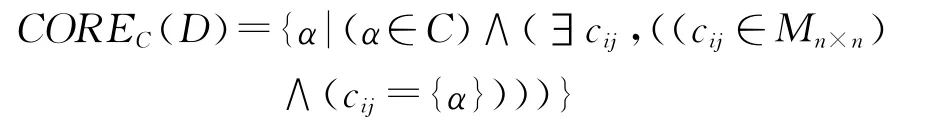
设决策表S=(U,A,V,f),A=C∪D,条件属性C相对于决策属性D的依赖度定义为

属性的重要度定义为

2.2 DSmT
1967年,Dempster提出证据理论,后来Shafer加以扩充和发展,所以也称证据理论为D-S证据理论[5~6]。2002 年,Dezert 和 Smarandache 提 出DSmT[5,7]。
设U={θ1,θ2,…,θn}是一个由n 个详尽的元素(其中元素可以交叠)组成的有限集合(称之为识别框架Θ),超幂集DU是通过对识别框架U中的元素进行并(“∪”)和交(“∩”)的运算产生的集合,满足如下条件:
1)φ,θ1,…,θn∈DU;
2)如果A,B∈DU,那么A∩B∈DU和A∪B∈DU;
3)只有元素满足条件1)和条件2),那么它们才属于DU。
幂集2U在∪算子中封闭,而DU在“∪”和交“∩”算子中封闭,则对于任意给定的有限集合U,始终有基card(DU)≥card(2U),即|DU|≥|2U|,即故我们称DU为超幂集[8~9]。
给定一个一般的识别框架U,定义一个基本概率赋值函数m:DU→[0,1],与给定的证据源有关,即

假设同一识别框架U 下的两条独立的、不确定的和高冲突的信源B1和B2和定义在DU(或DU的任意子集)上的两个广义基本概率赋值函数m1(·)和m2(·),经典DSm组合规则mMf(·)≡m(·)≜[m1⊕m2](·)定义为[10]
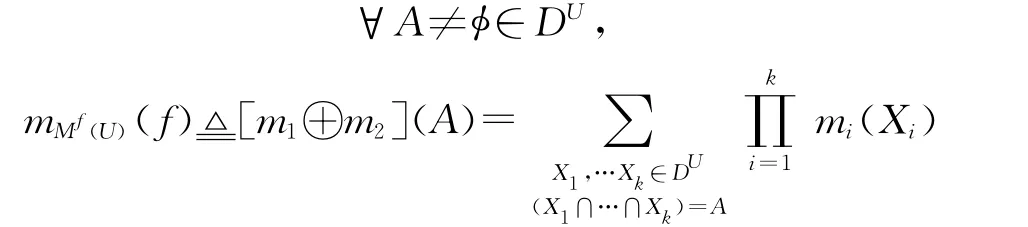
其中,mMf(U)(φ)=0。
3 融合故障诊断模型
本文融合粗糙集与DSmT进行故障诊断,首先应用粗糙集理论对不确定、不完备的故障信息进行处理,约简冗余的条件属性和属性值,获得约简决策表;然后计算约简条件属性的基本概率赋值,并进行规格化处理,最后应用DSmT获得融合推理诊断结果,具体流程如图1所示。

图1 融合故障诊断流程
4 应用实例
本文以某型机载电台装备的某一故障现象为例,验证以上方法的有效性。表1给出常见“电台不受控制”的故障现象,涉及到的故障征兆用条件属性“C”表示,C={+5V 电压C1,UUT收信端电压C2,UUT发信端电压C3,1553B总线C4},决策属性D={θ1,θ2,θ3},“θ1”代表同步模块,“θ2”代表前面板模块故障,“θ3”代表主控微机模块故障。现已提取8次测试数据如表1所示,这里第1~6次作为诊断样本,第7次为正常样本,第8次作为验证样本,并根据装备规定正常工作范围划分的区间进行离散化得到原始决策表(表3)。

表1 故障样本数据

表2 离散化区间

表3 原始决策表
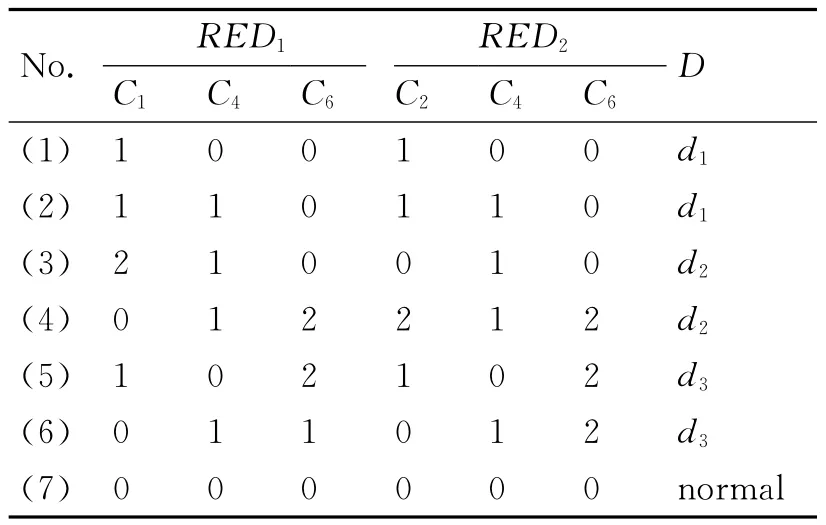
表4 约简决策表
对前6次故障数据计算差别矩阵,得相对核core={C4,C6}。在差别矩阵中,查找包含相对核的组合包含条件属性“C1”,“C2”,“C3”和“C5”。然后应用基于属性重要度的属性约简算法,分别数“C1”,“C2”,“C3”和“C5”的出现次数,发现“C1”和“C2”出现“6”次最多,因此得到相对约简,RED1={C1,C4,C6}和RED2={C2,C4,C6},约简决策表如表4所示。
然后,对应C1,C4,C6作为r1,r2,r3,C2,C4,C6作为R1,R2,R3,分别合成证据r和R,故障现象θ1,θ2,θ3,θ1θ3和正常分别作为识别框架的元素Θ1,Θ2,Θ3,Θ4,Θ5。
由RED1={C1,C4,C6}得到证据的基本概率赋值如表5所示。
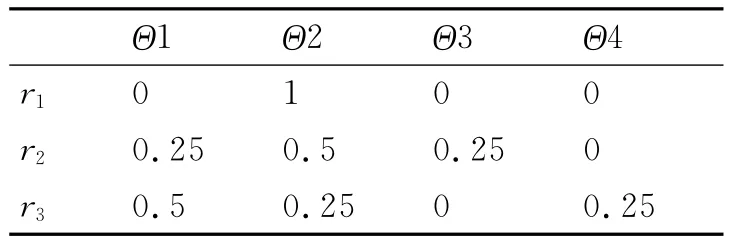
表5 基本概率赋值
计算RED1={C1,C4,C6}相对于 D 的属性重要度,得到SGF(C1,D)=2/7,SGF(C4,D)=2/7,SGF(C6,D)=4/7。然后,归一化处理得权重将其作为基本概率赋值分别为λ1=0.25,λ2=0.25,λ3=0.5,证据融合结果如表6所示。

表6 RED1融合结果
计算RED2={C2,C4,C6}的基本概率赋值如表7所示。
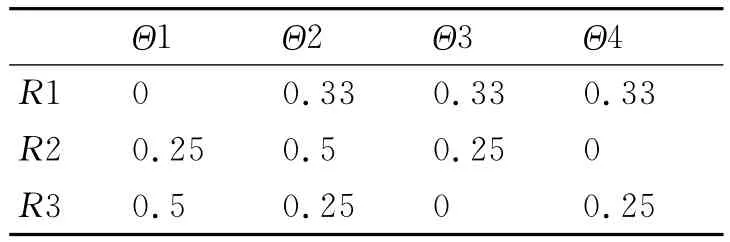
表7 基本概率赋值
计算RED2={C2,C4,C6}相对于 D 的属性重要度,得到SGF(C2,D)=6/7,SGF(C4,D)=4/7,SGF(C6,D)=4/7。然后,归一化处理得权重将其作为基本概率赋值分别为λ1=3/7,λ2=2/7,λ3=2/7,证据融合结果如表8所示。

表8 RED2融合结果
分别对表6和表8的融合结果应用DSmT合成规则,得到诊断结果如表9所示。

表9 DSmT融合结果
对比可得,Θ2对应的“d2”的故障可能性较大,与测试结果一致,验证本文方法的有效性。
5 结语
本文提出一种融合粗糙集和DSmT的故障诊断方法,对不确定、非精确信息具有一定的处理优势,并通过实例验证其有效性,从而为信息融合方法在装备故障诊断领域的应用提供了一条新的途径。
[1]段学刚.航空电子装备维修概论[M].北京:国防工业出版社,2010.
[2]Z.Pawlak.Rough sets[J].International Journal of Information and Computer Science,1982,11:341-356.
[3]苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008.
[4]孙秋野,张化光,刘贺男.基于粗糙集的变压器故障诊断方法研究[J].仪器仪表学报,2006,27(6):385-386.
[5]何友,王国宏,关欣,等.信息融合理论及应用[M].北京:电子工业出版社,2010.
[6]Dempster A.Upper and Lower Probabilities induced by multivalued mapping[J].Ann.Math.Statist.,1967,38:325-339.
[7]F.Smarandache,J.Dezert.Advances and applications of DSmT for information Fusion[M].Rehoboth:A-merican Research Press,2006:3-10.
[8]蒋海娜.基于Desert-Smarandache理论的故障诊断信息融合方法[D].杭州:杭州电子科技大学,2009.
[9]朱月君,张清华,邵龙秋,等.D-S证据理论在并发故障诊断技术中的研究进展[J].茂名学院学报,2009,6(19):55-59.
[10]李植良,徐晓滨,文成林.基于扩展证据理论的并发故障诊断方法[J].杭州电子科技大学学报,2008,6(28):107-110.

