基于PCA的脂肪肝超声RF信号特征选择

刘 映，林江莉，陈 科，罗 燕

(1.四川大学 材料科学与工程学院，成都 610064;2.四川大学华西医院 超声诊断科，成都 610041)

脂肪肝尤其早期脂肪肝是可逆转的，其早期诊断和治疗具有重要的临床意义。B超无创、无放射损伤，是脂肪肝诊断的首选检查方法。而脂肪肝的诊断对医生的临床经验有较强的依赖性，同时，还受设备等影响，因此，诊断主观性强、误诊率高。鉴于此，基于超声图像的脂肪肝辅助诊断具有重要的临床意义，通过提取图像的各类特征，进行脂肪肝分级识别，将提高临床诊断的准确性。

随着脂肪肝辅助诊断的研究，越来越多的特征参数被提出。但是，特征维数的增高也伴随着计算复杂度的提升、特征之间冗余度的增加。特征之间的相关性和冗余造成干扰信息，进而使得识别率不仅没有随着特征量的增加而增高，反而下降。因此，如何更有效地进行特征选择是目前研究的一个热点。

正常肝和脂肪肝的超声图像在视觉上的差异不明显，如图1所示，临床中的误判率高。基于超声图像的脂肪肝识别，由于没有形状特征，仅仅依靠亮度特征和差别细微的纹理特征，使得这类图像的识别具有较大的难度。

目前，基于超声图像的脂肪肝识别中，国内外提取较多的特征有:基于灰度共生矩阵的纹理特征、能量特征、射频信号包络、频谱偏移量等。林江莉等［1］提取了基于近远场灰度比的能量特征和基于灰度共生矩阵的纹理特征;Li GuoKuan等［2］提取了近远场灰度比、近远场光点密度、灰度共生矩阵和邻域灰度的差值矩阵;Xie Xiuqun等［3］基于超声RF信号，提取了信号包络、近似熵和近远场灰度比等特征。此外，还有研究者提取了低频小波系数、小波模极大值、频谱偏移量、散射系数等频域特征［4－5］。在大量的特征量中，如何选择适合的特征或特征组合，是研究的热点和难点。大部分的研究者都是直接给出所选的特征参数，并没有对所选特征进行评价择优。本文提取了脂肪肝超声图像原始射频(radio－frequency，RF)信号的参数特征，先通过t检验进行特征初步选择，再通过主成分分析进行特征组合。

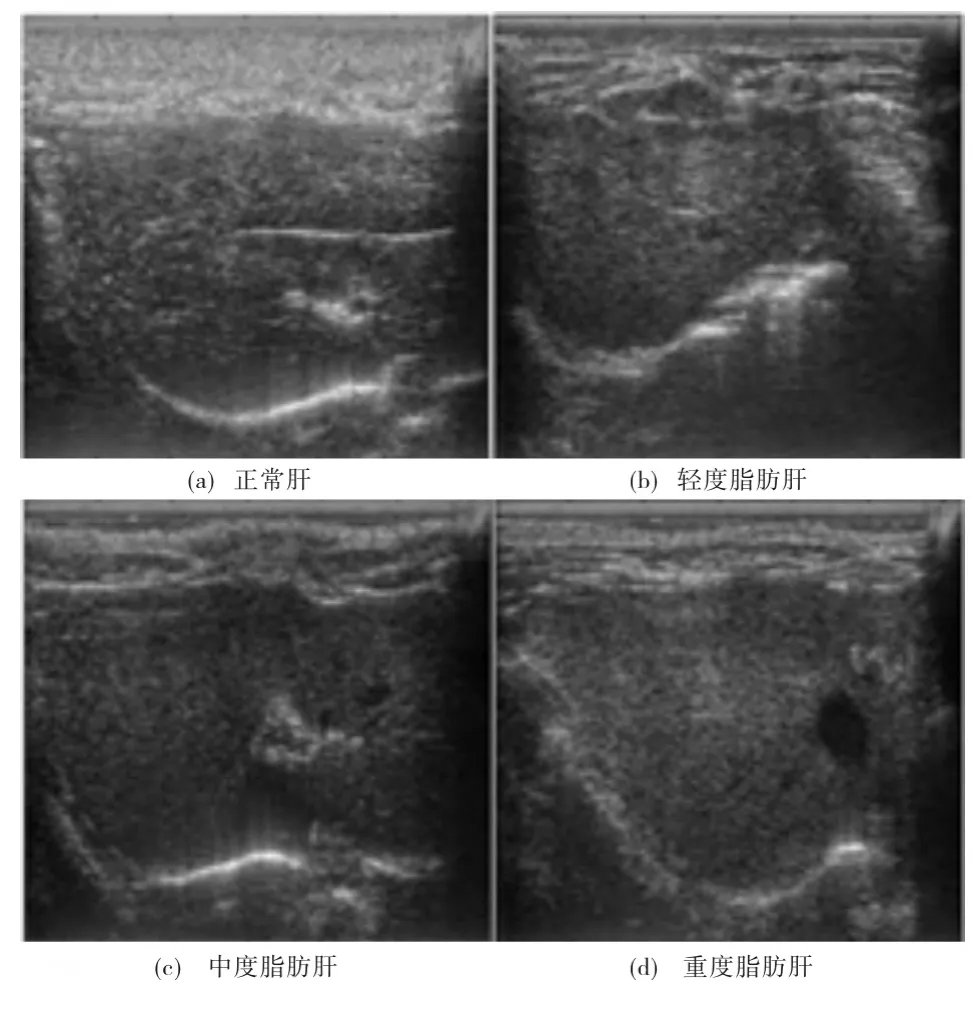
图1 正常肝与不同程度脂肪肝B超图像

主成分分析(principal component analysis，PCA)通过对原始特征数据的协方差矩阵或相关矩阵内部结构的研究，利用原始特征的线性组合形成主成分，在保留原始特征主要信息的前提下，降低特征向量维数［6－7］。其基本思想是将数据集转化为由维数较少的“有效”特征成分来表示，减少数据冗余，同时，保持原始数据包含的绝大部分信息内容，使其在统计意义下达到方差最优［8－9］。本文试图通过主成分分析法进行特征选择和组合，在保持绝大部分原始数据信息的前提下，降低特征向量维数，用降维后去冗余的特征向量进行脂肪肝超声图像的识别，以提高识别率。

1 PCA算法原理

通常，一个包含m个样本的集合可表示为［10］:

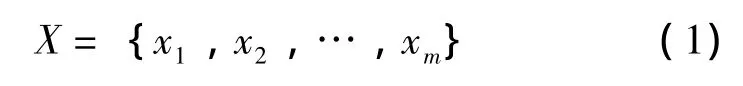
每个向量xi有n个特征，每个特征分别表示样本的一个诸如纹理或能量特征。

由于原始的特征向量矩阵中，每个特征的度量单位不同，数值的大小和变化幅度也不同，通常不能在同一水平进行比较分析。为此，应先对原始数据按特征分别做归一化，得到变换后的样本特征向量矩阵:

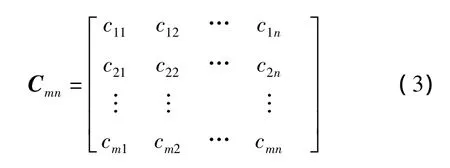
根据特征向量矩阵即可计算协方差矩阵:

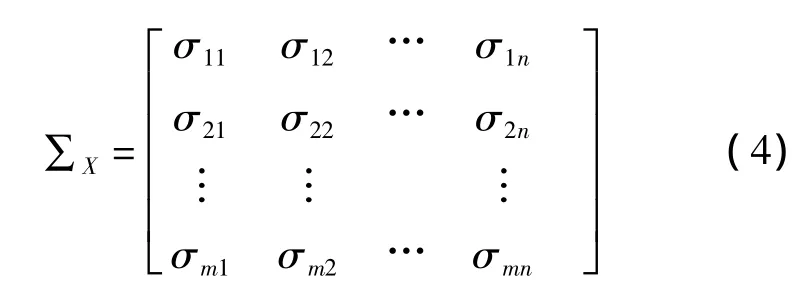
协方差矩阵中的(i，j)元素由下式给出:

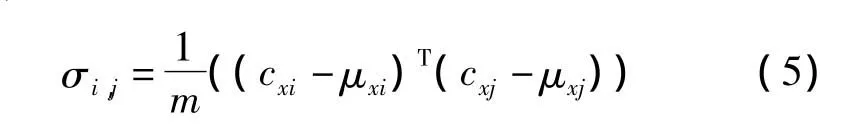
计算协方差矩阵的特征值及对应的特征向量。特征值λ1≥λ2≥…≥λn＞0对应的特征向量为:［u1，u2，…，un］。第k个主成分对原始特征向量矩阵的方差贡献率可以表示为:

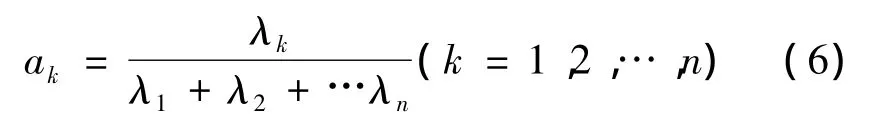
前p个主成分的累积贡献率表示为:

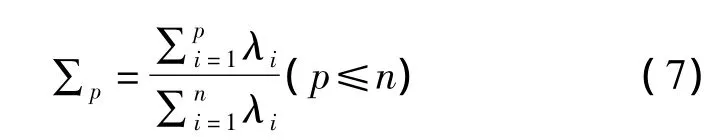
贡献率表示主成分在数据分析中所占比重的大小。当取前p个主成分代替原始特征参数时，p个主成分累积贡献率的大小体现这种取代的可靠性大小。当累积贡献率达到某一上限值∑T时，即∑p≥∑T，取前p个主成分，这样，在保留大部分原始特征向量信息的基础上，实现特征数据的降维。

2 方法

2.1 特征提取

1)信号采集。超声图像的采集避开血管和肋骨阴影等区域，识别选取固定大小的感兴趣(region of interesting，ROI)区域，并找出ROI区域对应的成像前的RF信号，如图2所示。所有特征参数都基于ROI区域的RF信号进行提取。

2)特征提取。本文提取了平均能量、近远场灰度比、包络特征(msr、sk、ku)和基于灰度共生矩阵的纹理特征(角二阶矩、对比度、相关性、方差、反差分矩、熵)共11个特征参数。

图2 ROI区域信号选取示意图

2.2 基于PCA的特征选择

1)对11个参数特征进行t检验，对特征进行初选，确定m个用于识别的特征，组成特征向量矩阵 Z=(z1，z2，…，zm)T。

2)对特征向量矩阵Z按列(特征)分别做归一化，计算归一化后矩阵的均值估计向量μ、标准方差估计向量σ及协方差矩阵Σ，计算协方差矩阵的特征值并从大到小排序。

3)设定累积贡献率上限值∑T，根据式(6)和式(7)，计算特征值λi的方差贡献率和累积贡献率。当累积贡献率大于或等于∑T时(本文设∑T=97 )，取出前p个主成分。

2.3 图像识别

图像识别可以视为从样本特征空间到类别空间的映射，识别器的训练就是通过一种学习算法获取一个预测。BP神经网络具有较强的非线性映射能力和自适应学习能力，在图像的分类识别中被广泛使用。但特征的选择和权重确定，仍对识别率有很大的影响，因此，本实验将结合主成分分析的结果，按照式(8)计算得到BP网络的输入值x'，进行脂肪肝超声图像的识别。

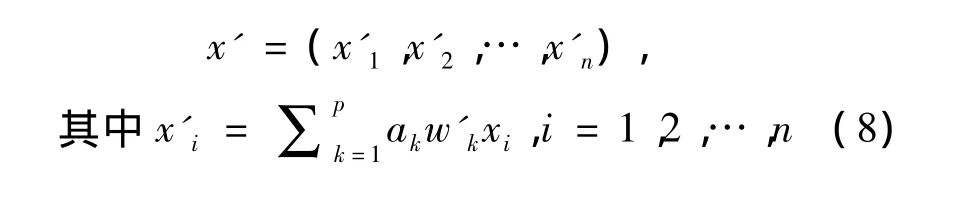
3 结果

本研究中的实验由四川大学华西医院超声科提供，选用Wistar大鼠，通过Siemens Acuson Antares超声仪的 VFX13－5探头(中心频率为 11.43 MHz)，采集大鼠肝脏的超声图像和对应的射频信号，并有对应的病理切片数据作为金标准。共筛选出106幅图像，其中正常肝39个、轻度脂肪肝31个、中度脂肪肝25个、重度脂肪肝11个。

为了确保所选特征对脂肪肝超声图像识别的适用性，首先，通过两独立样本均数的t检验(方差不齐时用t’检验)，将样本分为正常肝和轻度脂肪肝、中度和重度脂肪肝两组，t(t’)检验结果如表1所示。选用两组样本均数有差异的特征组成特征向量进行主成分分析。

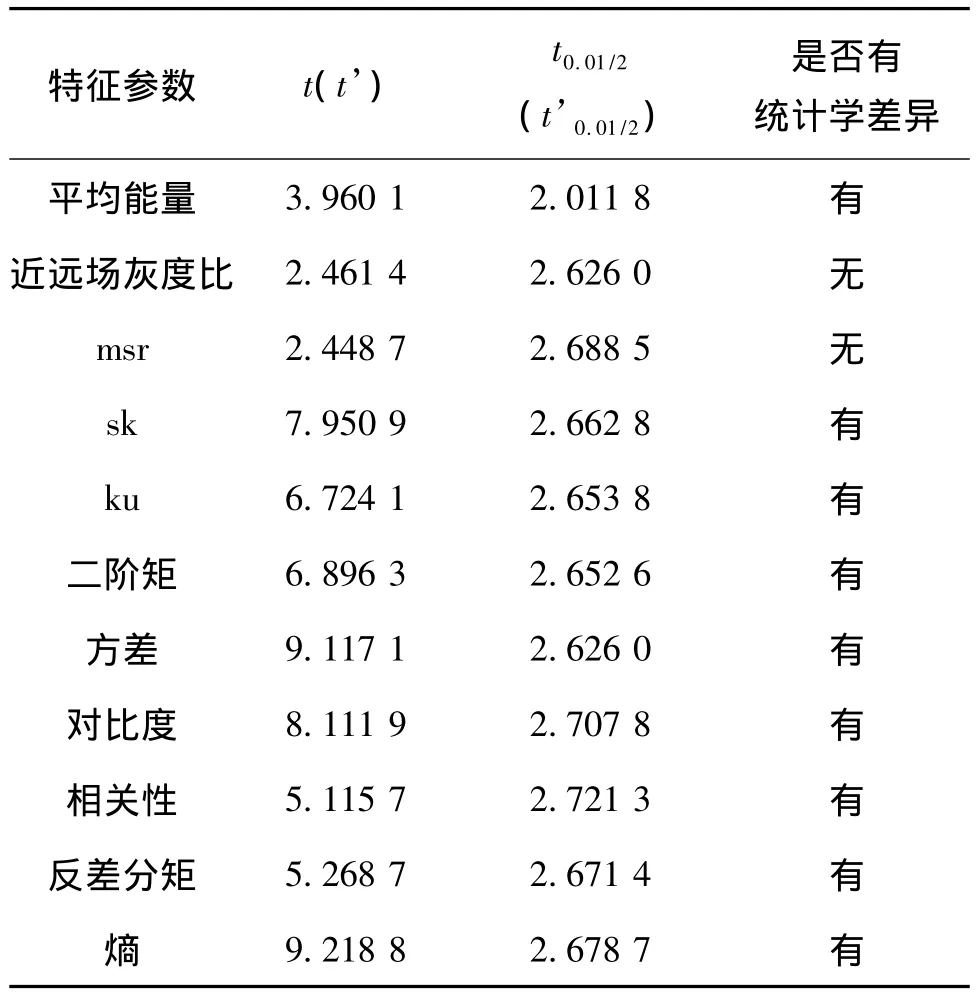
表1 样本均数的t检验结果

根据表1中的结果，实验选用平均能量、sk、ku和角二阶矩等共9个特征组成特征向量，计算样本图像特征向量矩阵的协方差矩阵，以及协方差矩阵的特征值和特征向量。特征值及贡献率如表2所示。

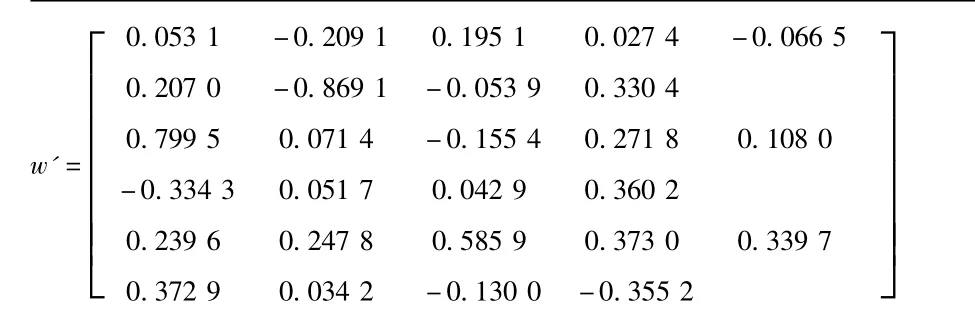
由表2可知，9个特征值的前三个的累积贡献率达到97.86，大于∑T，即前三个特征值的累积贡献率就可以达到要求。根据图像特征向量矩阵的协方差矩阵的特征向量，可得变换权重矩阵w’:

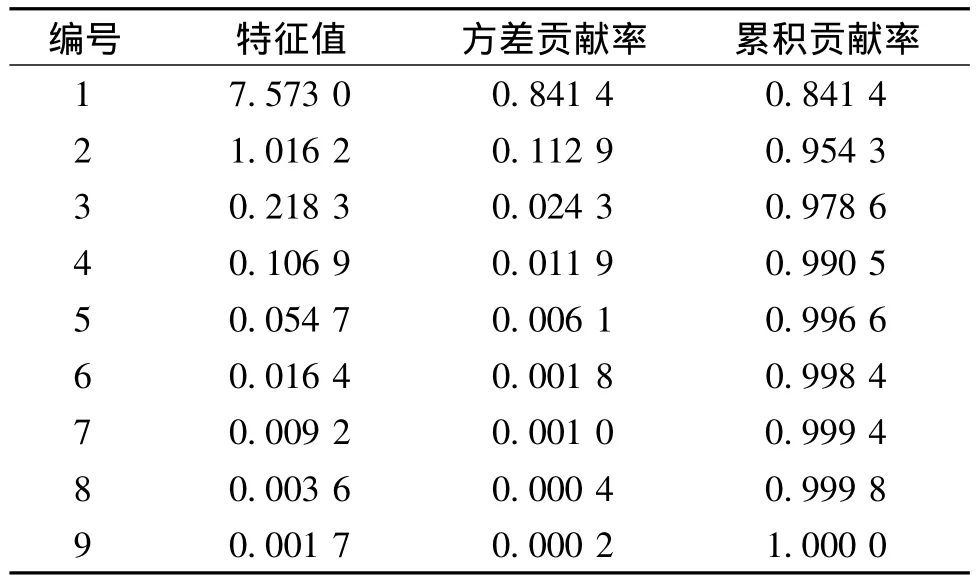
表2 协方差矩阵的特征值及贡献率

由于前p个特征值累积贡献率的大小，体现了前p个主成分代替原始特征参数的可靠性大小。实验中，前三个特征值的累积贡献率高达97.86，可见，此方法不仅降低了特征向量的维数，且保留了原始特征向量矩阵的绝大部分信息。

根据式(8)和式 (9)，结合特征贡献率和权重矩阵w’，计算得到BP网络的输入值，进行BP网络训练和识别。为验证基于t检验和主成分特征选择方法的优越性，实验将改进方法和选用所有特征直接进行BP网络训练识别的方法进行比较。实验选用106个样本，共进行12组实验，每组实验随机选取k个样本作为待识别样本，并将剩下106－k个样本作为训练样本，每组k取2～24不等。将所有样本分为正常肝和轻度脂肪肝、中度和重度脂肪肝两组进行训练和识别，并计算平均识别率，结果如图3所示。

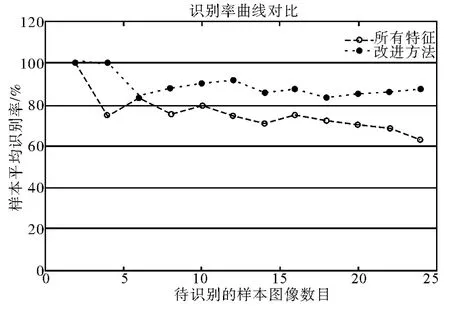
图3 两种方法的识别结果对比

由图3可以看出，改进方法的识别率明显高于选用所有特征基于BP网络的识别率。对12组实验的识别率求平均，改进方法的平均识别率为88.99，基于BP网络的平均识别率为75.63，改进方法的识别率提高了18 。

4 结束语

本文介绍了主成分分析的基本原理、数学模型及其实现，并将主成分分析算法结合两独立样本均数的t检验，应用于脂肪肝超声图像的识别。实验结果表明，特征向量协方差矩阵的前3个特征值的累积贡献率达97.86，保留了绝大部分的原始信息。结合主成分分析的特征贡献率和权重矩阵作为特征向量权重，应用于脂肪肝超声图像的识别，图像的平均识别率为88.99，较选用所有特征基于BP网络的平均识别率提高了18 。

［1］ 林江莉，汪小毅，李德玉，等.脂肪肝B超图像特征提取研究［J］.四川大学学报:工程科学版，2005，37(1):130－134.

［2］ Li Guokao，Luo Yu，Deng Wei，et al.Computer aided diagnosis of fatty liver ultrasonic images based on support vector machine［C］.30th Annual International IEEE EMBS Conference．［s．l．］:IEEE Press，2008:4768－4771.

［3］ Xie Xiuqun，Luo Yan，Quan Jierong，et al.SD rats’fatty liver tissue classification based on radiofrequency signal［C］.Jin D，Lin S.Advances in Computer Science and Information Engineering．［s．l．］:Springer Press，2012:643－647.

［4］ 刘志东，罗燕，林江莉，等.基于超声射频RF信号的脂肪肝分级量化方法［J］.四川大学学报:工程科学版，2011，43(Z1):160－164.

［5］ Liu Lanbo，John W Lane b，Quan Youli.Radar attenuation tomography using the centroid frequency downshift method［J］.Journal of Applied Geophysics，1988，40(1－3):105－116.

［6］ 徐克学.生物数学［M］.北京:科学出版社，1999:51－70.

［7］ 刘茂福，胡慧君，何炎祥.主成分分析在图像Zernike矩特征降维中的应用［J］.计算机应用，2007，27(3):696－698，702.

［8］ 刘小凤，李文.基于主成分分析的人脸特征提取［J］.企业家天地:理论版，2010(12):245－246.

［9］ 亓文永，叶心太.应用于图像特征识别的主成分分析算法［J］.科技信息，2008(22):30，19.

［10］ 周达丽.基于主成分分析的特征脸提取及人脸识别实现［J］.软件导刊，2012，11(5):162－164.