用单位阶梯函数求解变载荷梁挠度的方法
何春霞,吴雁平
(黄河科技学院 工学院,郑州 450063)
在工程结构分析与设计中,必须求解连续梁的内力和变形,以往的方法是在不同载荷作用处和不同截面位置分段,在不同段分别建立弯矩方程,进行积分,再联立相邻阶段的位移边界条件进行求解,整个过程繁琐,边界条件多。
单位阶梯函数是一种在一定的数值区间上取值为零,在其余数值区间上取值为1的函数,通常用H(x)表示。单位阶梯函数在通信及自动控制理论中有着广泛的应用,其最大的优越性体现在处理不连续问题中。不连续问题的分析通常需要在间断处分段,在每一段分别处理,然后在交接处通过边界条件求解,这种求解方法中间变量多,计算过程复杂。利用单位阶梯函数求解,不需要分段分别处理,可以用一个计算公式统一表达[1],从而使问题能够完整、简单地表述,在求解上也能够得到最大简化,并且利于编制程序实现电算化。本文用单位阶梯函数,在梁的全长范围内统一建立弯矩方程,进而推导出挠度的统一方程,由于不再进行分段求解,计算过程大为简化。
1 单位阶梯函数的定义与性质[2-3]
单位阶梯函数的表达式为:
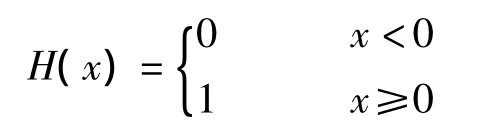
当自变量的分界点不为零时为延迟单位阶梯函数,表达式如下:
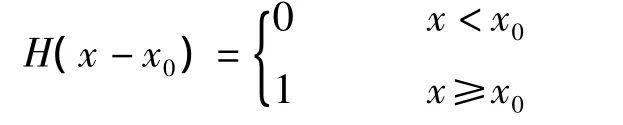
延迟单位阶梯函数可以起始任意函数,假设函数f(x),起始于x0点的任意函数表达式:
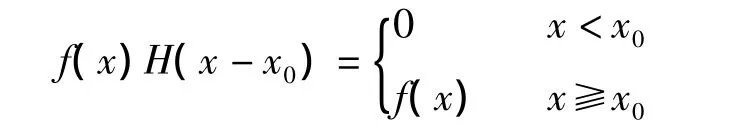
函数图像如图1所示。
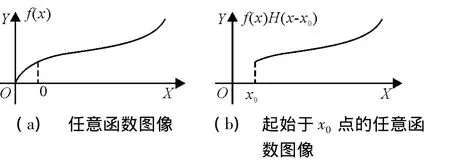
图1 延迟单位阶梯函数
延迟单位阶梯函数还可以表示某一段内函数,当a<b时,
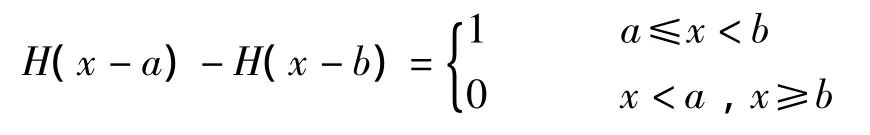
函数图像如2所示。
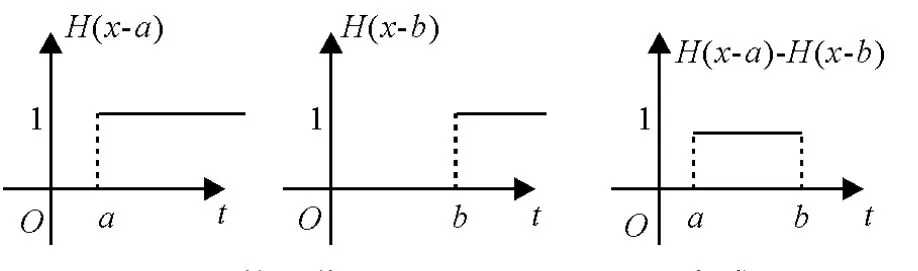
图2 函数图像H(x-a)-H(x-b)生成图
利用单位阶梯函数、延迟单位阶梯函数能将分段函数表示为一个式子[3],以便于分段函数的数据变换和微积分运算。
2 用单位阶梯函数表示结构中连续梁的内力方程
例1 设有一根连续的简支梁,计算简图和弯矩图如图3所示。其上受集中力F作用,设截面尺寸、材料参数不变。
自变量x从梁的左端开始,简支梁的弯矩方程为:
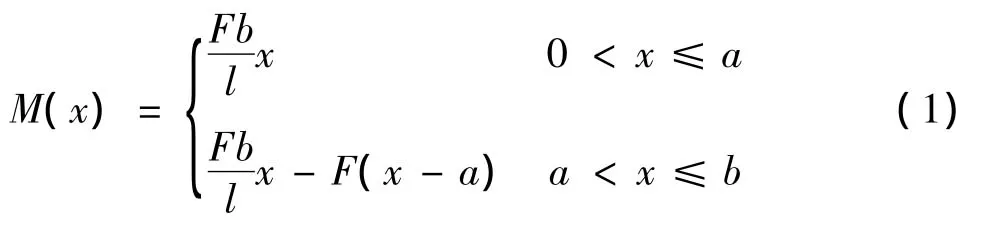
用单位阶梯函数将弯矩方程表示为统一的式子:
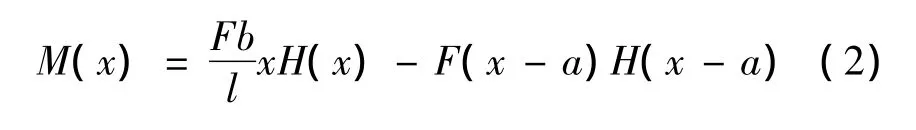
例2 设有一根连续的简支梁,计算简图如图4所示。其上受集中力F和均布载荷q作用,设截面尺寸、材料参数不变。
自变量x从梁的左端开始,简支梁的弯矩方程为:
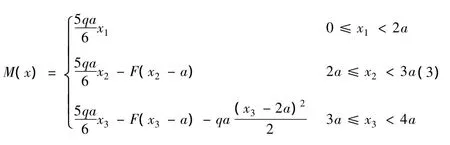
用单位阶梯函数将弯矩方程统一表示为:
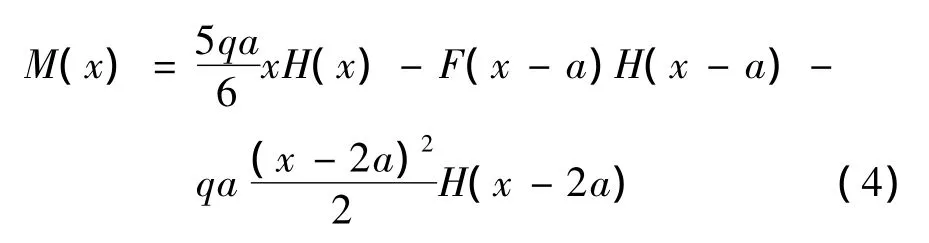
3 用单位阶梯函数求解连续梁的挠度
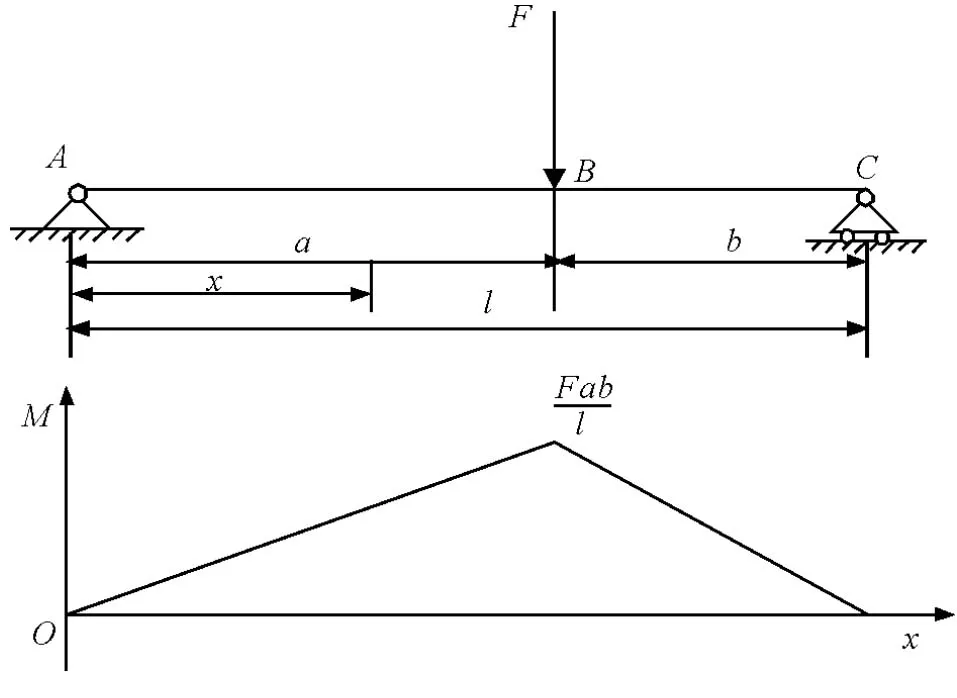
图3 计算简图和弯矩图1

图4 计算简图和弯矩图2
梁的挠度(w)是梁弯曲变形程度的度量。假设变载荷梁的截面尺寸不变,材料性质不变,则梁的抗弯刚度EI不变。弯矩与梁的挠度之间存在如下关系[4]:
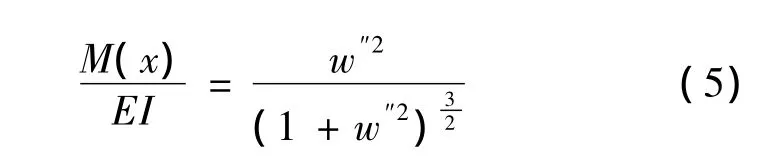
在梁小变形时,忽略挠度高阶导数的微量,上式简化为:
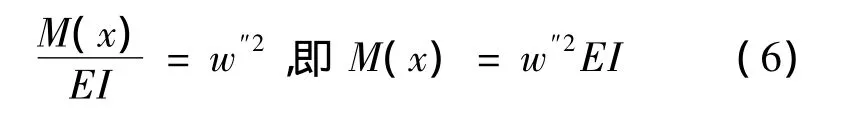
挠度方程为一元二阶线性齐次方程的解。将例1的弯矩分段方程组(1)代入式(6),分别进行两次积分,可求得AB段、CD段的挠度方程组为:
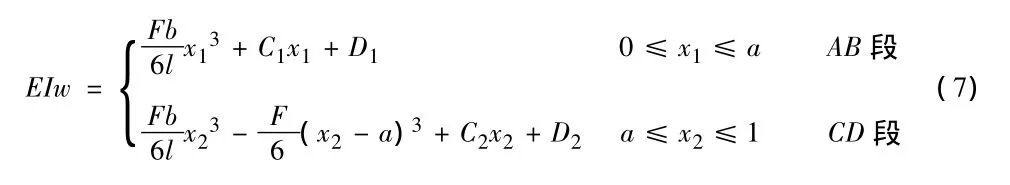
积分式中有四个积分常数,四个积分常数由约束边界条件确定。
梁为简支梁,在AB段,梁的左端为固定铰链支座,挠度为零,即x=0,w=0,得一个方程。在CD段,梁的右端为活动铰链支座,挠度依然为零,即x=l,w=0,得一个方程。由于梁连续,在B点的挠度连续,B点转角连续,上述积分式可得两个方程。四个未知量常数由上述四个方程求解。
若弯矩方程用阶梯函数统一表示的式(2)代入式(6),进行积分,得连续梁的统一挠度方程:
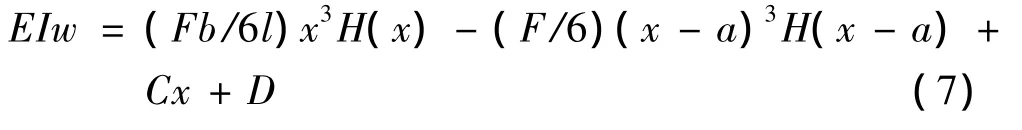
积分式中有两个常系数C、D。梁为简支梁,有梁的边界约束条件,梁的左端为固定铰链支座,挠度为零,即x=0,w=0,代入式(8),由阶梯函数的性质,x=0时,H(x-a)=0,则D=0。
梁的右端为活动铰链支座,挠度依然为零,即x=l,w=0,代入式(8),由阶梯函数性质,x=l时,H(x)=1,H(x-a)=1,则
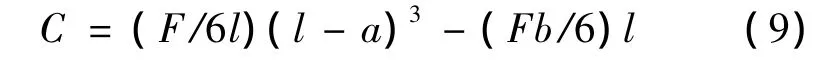
弯矩方程用阶梯函数表示的统一式子,中间变量的确定相对简化。
将上述求解的常系数C、D代入式(8),得连续梁挠度的统一方程:
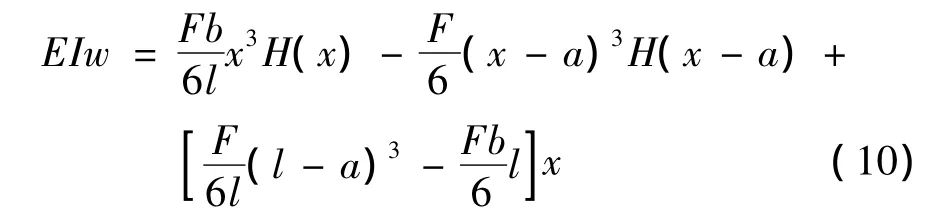
从上述两种求解方法的过程来看,弯矩方程用分段函数求解挠度,中间变量多,计算过程复杂;弯矩方程用阶梯函数表示的统一式子求解挠度,中间变量减少一半,计算过程规整,利于简化。对于变截面系数、多载荷作用的连续梁,如例2,采用阶梯函数表示的弯矩方程的统一式子来求解挠度问题将大大简化计算过程。
4 结束语
本文利用单位阶梯函数及其性质,对连续梁的挠度方程进行了求解,建立了连续梁挠度的统一方程,它克服了原来对变载荷问题要进行分段求解的不足,并且它的求解过程规整,有利于编制程序实现电算化,为这类问题提供了新的思路和方法。单位阶梯函数在力学领域中的应用还有待于进一步的研究。
[1] 荆振华.奇异函数在材料力学中的应用[J].辽宁省交通高等专科学校学报,1997,5(1):52-58.
[2] 汤志浩.单位阶梯函数的性质及其应用[J].湖南工程学院学报,2009,12(9):78-79.
[3] 徐彬.奇异函数建立高层结构分析模型的方法及应用[J].昆明理工大学学报,2000,25(6):106~109.
[4] 刘鸿文.材料力学I[M].5版.北京:高等教育出版社,2012:175~177.

