一种连续信号卷积的代数方法探究

田淙海，杨宗帅

(1．山西省气象局 山西省气象服务中心，太原 030002;2．北京爱洁隆技术有限公司 成都分公司，成都 610041)

《信号与系统》课程作为通信电子类专业必修的基础课程，很多学生反映入门较难［1］。主要原因在于:(1)初次接触这门课程，还没有和自己已有的知识体系关联;(2)理论抽象;(3)公式繁琐，较难理解。卷积是信号与系统理论的基础和灵魂。在线性时不变系统(linear time－invariant systems，LTI)中，我们把连续域中的卷积称为卷积积分，离散域中的卷积称为卷积和。然而，要正确地计算卷积并不容易，多数教材总是借助信号的移动来进行图解，不过需要花费大量的时间，且易遗漏或者出错。本文对一种计算连续信号卷积的代数方法进行了探究［2－5］。

1 卷积的定义

在连续信号与系统的时域分析中，一个重要的数学工具是一种特殊的积分运算，我们称之为卷积积分，简称卷积［6－8］。

设f1(t)和f2(t)是定义在(－∞，∞)区间上的两个连续时间信号，我们将积分

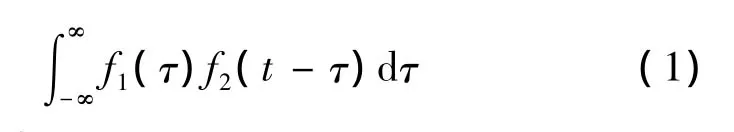
定义为f1(t)和f2(t)的卷积(convolution)，简记为

式(1)中:τ为虚设的积分变量。积分的结果为另一个新的连续时间信号。

2 卷积的运算

图像法计算卷积的优点是易于理解，计算分段信号的卷积非常实用，但缺点是计算时间长、易出错，而且对于很难画出图形的信号卷积，则无能为力［9－10］。

计算卷积的实质就是计算定积分。现举例对计算连续信号卷积的代数方法进行说明，并归纳计算连续信号卷积代数方法的步骤。

例1 计算(t+1)*ε(t－2)

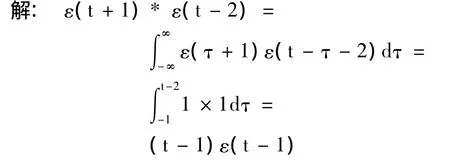
例2 计算 f1(t)=e－tε(t)，f2(t)=tε(t)，求f1(t)*f2(t)。

计算y(t)=f1(t)*f2(t)。

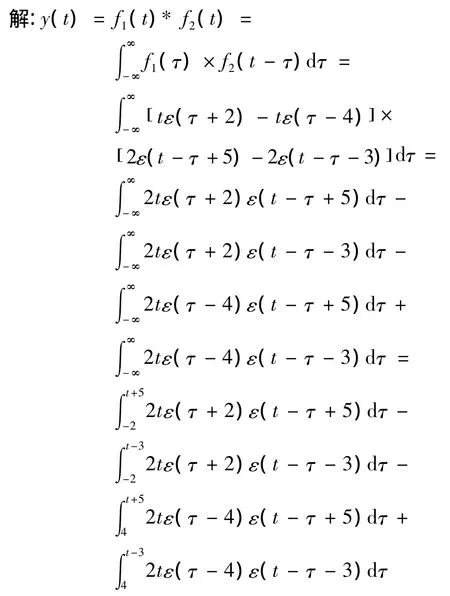
上式定积分，临界有意义的点有:t=－7，t=1，t=－1，t=7。

1)当t＜－7或t≥7时，y(t)=0;

2)当－7≤t＜－1时，

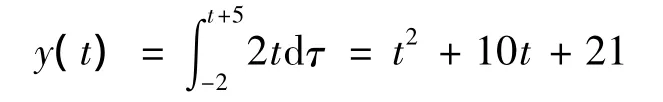
3)当－1≤t＜1时，

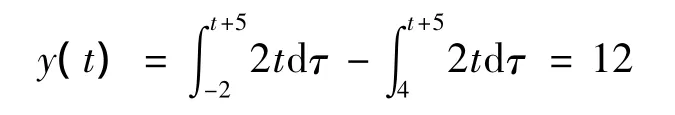
4)当1≤t≤7时，

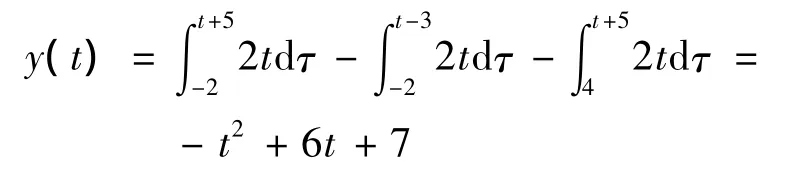
综上所述，

从上面的3个例子可以看出，计算连续信号卷积的代数方法比较简单，更重要的是我们对定积分的运算非常熟悉，理解起来相对容易，且计算不易出错。计算连续信号卷积的代数方法的步骤可分为三步:(1)根据卷积的定义代换，t→τ，t→t－τ;(2)化为定积分，找出使ε(τ)为1的τ的范围，当然τ可以为一个代数式;(3)找出定积分有意义的临界t值，分段计算定积分。

3 结束语

实现连续信号卷积的方法有很多，而且各有特点。本文对一种计算连续信号卷积的代数方法进行了探究，发现计算连续信号卷积的代数方法运用起来非常简单、方便，更为重要的是可以将卷积运算直接转化为我们熟悉的定积分运算。

［1］ 陈生潭，郭宝龙，李学武，等.信号与系统［M］.3版.西安:西安电子科技大学出版社，2008:47－50，82.

［2］ 杨永生，赵梅.从时域和频域两种角度探讨卷积积分［J］.通信技术，2010(11):165－166，168.

［3］ 李相国.“数字信号处理”中的线性卷积求解［J］.中国电子教育，2013(3):41－46.

［4］ 徐洁婷，王光.超广义函数空间中的乘积和卷积运算［J］.中北大学学报:自然科学版，2011(1):56－59.

［5］ 唐建锋，杨辉，罗湘南.信号与系统中卷积计算方法探讨［J］.科技信息，2012(4):16.

［6］ 王晓翔，黄静，梁忞飞.关于卷积的运算规则及存在性［J］.电气电子教学学报，2012(2):39－42.

［7］ 王晓平.卷积积分的基本计算方法［J］.常州工学院学报，2002(4):54－57.

［8］ 付会凯.卷积积分运算方法探讨［J］.黑龙江科技信息，2008(25):5.

［9］ 雷学堂，徐火希，董金光，等.用图解快速定限法确定卷积的积分限［J］.黄冈师范学院学报，2004(6):40－44.

［10］ 林让起，徐瑞标.卷积性质的代数证明［J］.湖州师范学院学报，2010(1):116－118.