某核废物处置预选区中核素迁移模拟研究
李 寻, 杨泽平, 李金轩, 张卫民, 李小燕
(1.东华理工大学核资源与环境省部共建国家重点实验室培育基地,江西南昌 330013;2.东华理工大学水环学院,江西 南昌 330013)
我国于1985年9月制定了“中国高放废物深地质处置研究发展计划”(即DGD 计划),并于1986年2月开始实施(杨立基,1992)。该计划以高放玻璃固化体和超铀废物以及少量重水堆乏燃料为处置对象,以花岗岩为处置介质,提出在2040年建成高放废物处置库的设想(王驹,2004)。但无论多么完整的花岗岩体都含有不规则交错裂隙,无论是核废物的正常排放还是事故泄露,这些交错裂隙都是核素进入生物圈之前的主要迁移通道。因此,研究核素在裂隙介质中的迁移规律是高放废物深地质处置库安全评价中极为关注的问题。
目前研究裂隙介质中核素迁移问题的数学模型主要有以下几种:等效连续介质模型(ECM)、离散裂隙网络模型(DFN)、双重连续介质模型(DPM)和随机模型(SCM)等(王锦国,2005),王月英(2011)基于前述模型,提出ECM-DFN、DPM-DFN等横向耦合模型。而其中的双重连续介质模型常用于解决大尺度问题,而核废物深地质处置中核素迁移范围涵盖了处置库外沿与生物圈之间的区域,且时间跨度大(罗嗣海等,2005),因此本文采用双重连续介质模型来模拟核素在地质屏障中的迁移,即在地质屏障中,把一些大的且连通性好的裂隙视为核素迁移的通道(即裂隙域),而裂隙两侧一定范围内虽含有众多小裂隙但因其连通性不好、导水性差而视为基质域。Moreno 等(1985)在一端为定物质通量连续注入源的条件下,得到了描述单裂隙中溶质运移的解析解;Maloszewski 等(1990)给出了瞬时注入和可逆瞬时吸附条件下单裂隙中溶质运移的解析解;王岩等(2006)得到了一端具有分时注入源的溶质运移的解析解;在Neretnieks(2006)及Shih(2007)对于放射性核素在单裂隙中迁移探讨的基础上,李寻等(2010)则对于注入源为指数衰变条件下的核素运移问题进行了求解,而本文则是在此解析解的基础上,将裂隙介质按其导水系数的随机分布概化为由多途径所构成的虚拟介质,各运移途径仍可看作具有独立参数的平行板单裂隙,按其导水系数的分布概率进行叠加来研究核素在裂隙介质中的迁移规律,进一步探讨了裂隙网络系统中的核素迁移问题;最后通过具体的算例探讨了裂隙介质多途径运移模型在高放废物处置系统安全性能评价中的应用。
1 基于双重介质理论的单裂隙核素迁移模型及其解析解
1.1 物理模型
在研究中,考虑核素在饱和多孔岩石中一条细长裂隙中迁移并满足以下假设条件:①裂隙中水流流速为常数;②裂隙的宽度为常数且远小于裂隙的长度(2b≪L);③裂隙中的横向扩散和弥散在整个裂隙宽度上瞬时完全混合,并忽略裂隙壁本身对核素的阻滞作用;④沿着裂隙的运移比在基质中的运移快得多;⑤发生于岩块中的核素扩散沿垂直于裂隙的方向进行;如图1 所示。
在模拟过程中,考虑以下过程:①在裂隙域中,核素沿着裂隙轴向的对流迁移和分子扩散、纵向机械弥散;②核素从裂隙域向基质域的分子扩散;③在基质域中,岩块表面和岩块本身对核素的吸附作用;④核素的放射性衰变。

图1 单裂隙介质中核素迁移示意图Fig.1 Schematic illustration of solute transport in s single fracture
1.2 数学模型的建立
综合考虑上述的假设条件,图1 所示的运移过程可以通过两个耦合的一维方程来描述,分别为描述核素在裂隙域中和基质域中迁移的方程,二者是通过在交界面处流量和浓度的连续性来耦合(Moreno et al.,1985;王岩等,2006)。
根据质量守恒,考虑核素的放射性衰变,并假定基质域中的吸附为线性等温吸附,可以得到分别得到裂隙域和在垂直于裂隙方向上核素在基质域中的基本迁移方程(王岩等,2006),即

式中,c 为裂隙中溶质的浓度,等于c(x,t);cj为基质域中溶质的浓度,等于cj(x,z,t);t 为时间;x 为裂隙轴向方向的坐标;z 为与裂隙轴向垂直方向的坐标;u 为裂隙中溶质运移的平均速率;DL为裂隙中的纵向弥散系数DL= αLu + Dm,其中Dm为在自由水中溶质的分子扩散系数,αL为裂隙轴向方向上的弥散度;Dj为基质域中的有效扩散系数;λ 为放射性核素的衰变常数;θ 为基质域多孔岩体的孔隙率;F 为能允许溶质扩散到岩石中去的裂隙壁表面积占裂隙壁总面积的比例。R 为裂隙域中的迟滞系数其中Kf为裂隙域中的分配系数;Rj基质域中的迟滞系数其中Kj为基质域中的分配系数,ρb为岩石的干密度。
对于方程(1)和(2),其初始条件为:

裂隙的上、下游边界记为:

式中,c0为上游边界处输入浓度的初始值;k 为上游边界处输入浓度的源衰减常数。
而在基质域中,其边界条件写为:
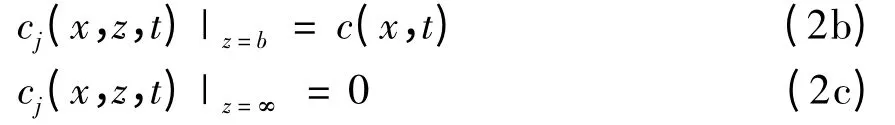
方程(2b)表示了在裂隙壁处,多孔基质域中的溶质浓度与裂隙域中溶质浓度相等。
1.3 解析解
求解由裂隙域和基质域中方程(1)、(2)耦合得到的数学模型,可以得到该数学模型的通用解析解(李寻等,2010)。
在这里,为书写方便,记:

2 预选区场地分析及多途径核素迁移模型
到目前为止,我国已选定西北某地作为高放废物地质处置的重点预选区。经过勘察发现区内华力西期侵入的花岗岩分布广泛,其厚度大,虽受多期构造运动的影响,断裂构造十分发育,但这些构造均属非活动构造,对区内的地质稳定性不构成影响(郭永海等,2001)。从工程屏障中释放出来的核素随地下水在地质屏障裂隙中经过对流、吸附、水动力弥散、衰变等作用后进入导水断层,顺着导水断层慢慢的向地表迁移,最后进入到地质屏障以外的生物圈,从而威胁各种生物的健康。
研究时考虑真实裂隙导水性能的各向异性,将随机分布的导水系数离散化,每一条途径代表一系列具有相同导水性的通道。Ijiri 等(1998)已经通过数值实验证实了一维多途径模型能合理地近似描述核素在一个复杂的、随机生成的三维裂隙网络系统中的迁移,因此可以把裂隙网络的运移通道按照其特征进行分组,而具有相同特征的每一组可视为光滑平行板单裂隙模型,进而采用单裂隙模型进行模拟。在本文中进行模型概化时,根据裂隙隙宽的分布情况将其离散为若干个区间,则对应有若干条运移途径,每一区间的平均隙宽即为该运移途径所对应的平面单裂隙的隙宽。
因此在对裂隙网络系统中核素相对浓度进行模拟计算时,首先根据基于双重介质理论的平板单裂隙迁移模型分别计算每条运移途径单独工作时在裂隙系统中相对浓度的分布;然后将各运移途径在某处的相对浓度按其隙宽的分布频率进行叠加就可得到整个裂隙系统在某处核素的相对浓度,即

裂隙域:式中,i 为运移途径的编号;N 为运移途径的总条数为第i个运移途径单独工作时的相对浓度;Pi为第i个运移途径所对应的隙宽分布概率为整个裂隙系统中任意时刻、任意位置处的相对浓度。
3 多途径核素迁移模型的应用
3.1 相关参数取值
本文以国内在花岗岩中研究较多的放射性核素Cs-134、Co-57、Tc-99 为研究的对象(其特征见表1),西北某核废物处置库预选区花岗岩裂隙为载体,在现阶段研究成果的基础上,对其在地质屏障中的迁移进行模拟研究。
李春江等(1999a,1999b,2000),苏锐(2000)通过实验研究了核素Cs-134、Co-57、Tc-99 在单裂隙花岗岩柱中的运移特性,取得其相关的扩散系数、迟滞系数等参数。选用参数时,从安全角度考虑,均选择有利于核素迁移的值,如迟滞系数、基质扩散系数等取参考文献中的小值,如表1 所示。单裂隙花岗岩柱,被沿岩柱轴心的天然裂隙面切割,上下地面打磨光滑,柱长60 ~170 mm,直径50 mm 或60 mm 不等(苏锐,2000)。

表1 研究核素的相关参数Table 1 Parameters of considered nuclides
根据李亚萍(2005)对该核废物处置场预选区花岗岩地表137 5个裂隙隙宽的统计分析得:0.1 ~0.3 cm 宽度的裂隙占78 %,0.3 ~0.5 cm 的占12%,大于1 cm 的裂隙少于5 %。按照定义:该区域花岗岩的裂隙主要属于开裂型。但由于随着深度的增加(上部荷重增加)使得裂隙隙宽减小。考虑深度的影响设处置库周围的隙宽分布范围为米之间,这与JNC(2000a)在深部矿井中所取得的结果基本一致。
对平行板单裂隙而言,导水系数和裂隙隙宽之间满足立方定律(Snow,1968),而对实际的粗糙裂隙,本文引用JNC 的经验公式 来确定不同隙宽对应的导水系数(JNC,2000b),即:

式中,2bi为第i个运移途径所对应的平面单裂隙的隙宽;Ti为第i个运移途径的导水系数;c 为经验公式的常系数,c = 2。
由于国内对高放废物地质处置研究起步较晚,到目前为止还没有处置库预选场区的野外示踪试验,仅对附近中低放废物处置库进行初步调查获得了其水力梯度为0.57%(袁革新等,2008),而实验室得到的水力坡度对获得野外水力坡度没有任何意义的,所以在这里结合附近的数据以及日本在低渗透花岗岩中水力坡度的调查(JNC,2000b),从安全角度考虑,取水力坡度J = 0.01。根据式(5)即可求得在各种不同隙宽下的导水系数,进而各运移途径的地下水流速可根据该运移途径的导水系数、隙宽及地下水水力坡度按达西定律确定,即

式中,ui为第i个运移途径的地下水流速;J 为地下水的水力坡,本研究中取J = 0.01。
有了地下水流速后,各运移途径裂隙的纵向弥散系数按式(7)得出(刘兆昌等,1991):

式中,DLi为第i个运移途径裂隙的纵向弥散系数。αL为裂隙轴向方向上的弥散度,αL= 0.017x1.5(x为0.01 ~3 500 m)(JNC,2000b)。
岩石孔隙度以及岩石密度取的是其平均值(苏锐,2000;李春江等,2000),具体取值见表2。裂隙系统的其他物理参数如允许核素扩散到岩石中去的裂隙壁占裂隙壁总面积的比例、岩石的孔隙度、岩石密度以及岩石的有效扩散系数见表2。
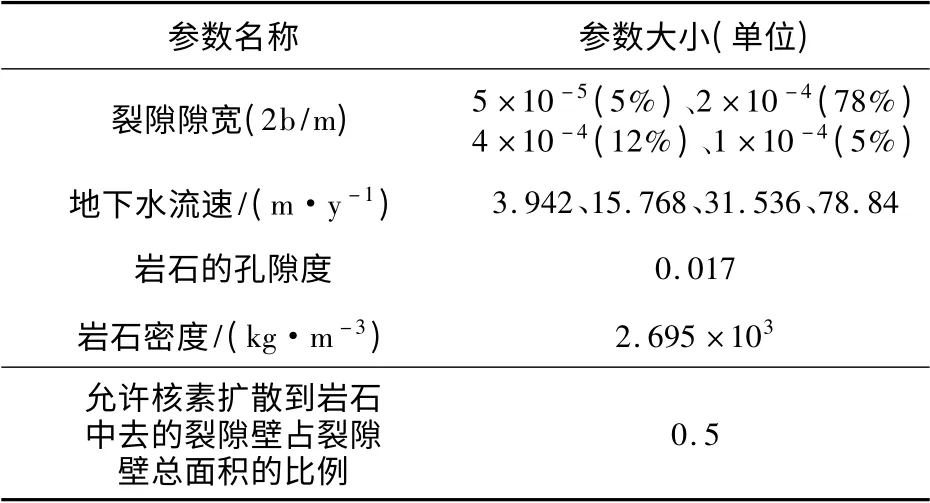
表2 裂隙系统的相关参数Table 2 Parameters of fracture system
3.2 模拟结果及分析
根据前述裂隙系统中核素迁移的一维多途径概念模型,核素的衰变常数、迟滞系数(表1),就该地地表花岗岩裂隙隙宽分布情况,分别取隙宽为2×10-3m(78%)、4 × 10-3m(12%)、5 × 10-4m(5%)与1 ×10-2(5%)(表2),裂隙系统的其余相关参数如孔隙度、密度等如表2 所示,模拟了Cs-134、Co-57、Tc-99 这三种核素在该预选区地质屏障中的迁移情况,具体如图2、3 所示。
首先,模拟了Cs-134、Co-57、Tc-99 这三种核素在1 ×102、1 ×103和×104年时相对浓度在裂隙中的变化情况,如图2 所示。从图2 可以看出,在同一位置处,核素的相对浓度随着迁移时间的增加而增加。对比图2 中各核素的相对浓度值可知,在同一位置同一模拟时间Tc-99 在裂隙域中的相对浓度是最小的,也就是说它在同样介质中的迁移是最慢的,而Cs-134 的迁移是最快的;对比这些数据还可以发现,在其它条件相同的情况下,在同一位置同一模拟时间,这些核素在裂隙域中相对浓度的分布并不是按迟滞系数的关系来排列的,说明核素在裂隙域中的相对浓度大小还与其半衰期、基质域中的扩散系数有关。
图3 则表明在同一时刻,核素在裂隙中的相对浓度随着迁移距离的增加而减小;在迁移距离较小时(x =400 m),三种核素的相对浓度在约4 ×105年后变化比较小,基本趋于比较稳定的状态;而在迁移距离较大时,达到这种稳定状态所需的时间要大得多。

图2 裂隙系统中核素相对浓度与距离的关系图Fig.2 Relationship of relative concentration and the distance in fracture system

图3 裂隙系统中核素相对浓度与时间的关系图Fig.3 Relationship of relative concentration and the time in fracture system
值得注意的是:上述模拟过程中所采用的参数都是在实验室尺度下得到的,而Bradbury 等(1985)、Ohlsson 等(1995)、Rebour 等(1997)、Xu S.等(2001)都通过试验指出室内实验得到的扩散属性与野外现场试验有相当大的差异。Bradbury 等(1985)指出:首先,如果岩样很细时(小于5 cm),由于在切样的过程中人为地将不连通的孔隙给打通了,在穿透-扩散实验会高估孔隙的连通性2倍;其次,在天然约束条件下所得到的原位扩散参数比在实验室得到的结果要低倍。Birgersson 等(1990)也通过在Stripa 矿井360 m 深处进行的扩散实验指出应该小心使用在实验尺度下所得到的参数。
不管是瑞典乏燃料与核废物管理机构(SKB)对描述Äspö 假定地下处置库中的流动与对流运移的研究,还是对DECOVALEX Ш 项目中两个试验实例的研究都表明:成功的数值模拟不仅与数值方法的选择有关,更取决于岩体准确的水文地质特性描述与实验系统本身。所以,对于本次模拟所得到的结果仅供参考。
4 结论
(1)将裂隙系统视作双重介质模型,建立了一端具有指数衰变注入源的基质域-裂隙域中溶质随地下水迁移的数学模型,利用拉普拉斯变换得到了相应的解析解;针对低渗透花岗岩中核素迁移的复杂性,将双重介质理论与随机理论有机地结合起来,提出采用基于隙宽分布概率的一维多途径核素迁移模型来模拟裂隙系统中的核素迁移问题。该模型能充分考虑裂隙系统的非均质性,可较合理地描述核素在一个复杂的、随机生成的裂隙网络系统中的迁移。
(2)在对西北某核废物处置场预选区地水文地质条件分析的基础上,获取相关参数,利用一维多途径核素迁移模型,选取国内在花岗岩中研究较多的核素Cs-134、Co-57、Tc-99,根据隙宽的统计规律模拟了这几种核素的相对浓度随模拟时间、迁移距离的变化规律。模拟结果表明,在模拟条件下,Cs-134 的迁移是最快的,而Tc-99 迁移是最慢的。并指出了核素在裂隙域中的相对浓度大小不仅与迟滞系数有关,还与其半衰期、基质域中的扩散系数有关以及实验室参数应用到野外模拟所存在的一些问题。
(3)应用一维多途径核素迁移模型,不仅可以预测模型所描述条件下核素在裂隙系统中相对浓度的分布情况和发展趋势,还可以研究该模型条件下的各参数对核素迁移的影响,对于深入了解各种因素对核素迁移的影响提供了有力的支持,同时也为实验室研究中模型参数的选定奠定了基础。
郭永海,杨大笑,刘淑芬.2001. 高放废物处置库甘肃北山预选区水文地质特征研究[J].铀矿地质,17(3):184-189.
李春江,郭志明,林漳基.1999a. 花岗岩单裂隙中核素125I-、134Cs+的弥散渗透实验[J].水文地质与工程地质,6:45-51.
李春江,郭志明,林漳基,等. 1999. 花岗岩体单裂隙中核素125I-、
134Cs+的弥散渗透实验[J].水文地质工程地质,35(6):45-47.
李春江,苏锐,陈式,等.2000. 花岗岩单裂隙中核素迁移的研究II.扩散系数的测定[J].核化学与放射化学,8:190-192.
李寻,张土乔,李金轩.2010. 单裂隙介质中核素迁移模型的解析解及其应用[J].哈尔滨工业大学学报,42(12):1559-1563.
李亚萍.2005.甘肃北山花岗岩裂隙几何学特征研究[D]. 北京:中国地震局地震研究所.
刘兆昌,张兰生.1991.地下水系统的污染与控制[M].北京:中国环境科学出版社:66-92.
罗嗣海,钱七虎,李金轩,等.2005.高放废物深地质处置中的多场耦合与核素迁移[J].岩土力学,25(增刊):264-270.
苏锐.2000.花岗岩体重核素迁移特性研究[D]. 北京:核工业北京地质研究院.
王锦国,周志芳.2005.裂隙岩体溶质运移模型研究[J]. 岩土力学,26(2):270-276.
王驹.2004.我国高放废物深地质处置战略规划探讨[J].铀矿地质,20(4):196-212.
王岩,梁冰.2006.裂隙岩体地下水溶质运移规律的研究[C]//段祥宝,谢兴华,速宝玉编,水工渗流研究与应用进展——第五届全国水利工程渗流学术研讨会,郑州,黄河水利出版社:455-461.
王月英,姚军,黄朝琴,等.2011.裂隙岩体流动模型综述[J].大庆石油学院学报,35(5):42-48.
袁革新,陈剑杰.2008.罗布泊西北缘低中放废物处置场选址初步研究[C]//中国岩石力学与工程学会废物地下处置专业委员会等,第二届废物地下处置学术研讨会论文集,敦煌:467-472.
Birgersson L,Neretnieks I. 1990. Diffusion in the matrix of granitic rock:field tests in the Stripa mine[J],Water Resource Research,26(11):2833-2842.
Bradbury M H,Stephen I G. 1985. Diffusion and permeability based sorption measurements in intact rock samples[J]. Materials Research Society Symposium Proceedings,50:81-90.
Ijiri Y,Swada A,Webb E K,et al,1998,Radionuclide migration analysis Using a discrete fracture network model[C]//Proceeding of the Materials Research Society 1998 fall meeting-Scientific Basis for Nuclear Waste Management Ⅻ,Boston:Materials Research Society,(556):586-592.
Japan Nuclear Cycle Development Institute (JNC).2000a.H12,Project to Establish the Scientific and Technical Basis for HLW Disposal in Japan (Supporting Report 1:Geological Environment in Japan),JNC TN1410 2000-002[R],JNC,Tokai,Japan,April 2000a.
Japan Nuclear Cycle Development Institute (JNC,2000b.H12:Project to Establish the Scientific and Technical Basis for HLW Disposal in Japan (Supporting Report 3:Safety Assessment of the Geological Disposal System),JNC TN1410 2000-004[R],JNC,Tokai,Japan,April 2000b.
Maloszeeski P,Zuber A. 1990.Mathematical modeling of tracer behavior in short-term experiments in fissured rocks[J]. Water Resour Res,26(7):1517-1528.
Moreno L,Rasmuson A.1985.Contaminant transport through a fractured porous rock:impact of the inlet boundary condition on the concentration profile in the rock matrix[J]. Water Resource Research,21(7):951-958.
Neretnieks I. 2006.Fast method for simulation of radionuclide chain migration in dual porosity fracture rocks[J]. Contaminant Hydrology,88(4):269-288.
Ohlsson Y,Neretnieks I. 1995.Literature survey of matrix diffusion theory and of experiments and data including natural analogues,SKB Technical Report 95-12[R]. Stochholm,Swedish Nuclear Fuel and Waste Management Company(SKB),
Rebour V.,Billiotte J. 1997. Molecular diffusion in water-saturatd rocks:a new wxperimental method[J]. Journal of Contaminant Hydrology,(28):71-93.
Shih D C F. 2007.Contaminant transport in one-dimensional single fractured media:semi-analytical solution for three-member decay chain with pulse and Heaviside input sources[J]. Hydrol. Process,21(16):2135-2143.
Snow D T.1968. Rock fracture spacings,openings and porosities[J].Journal of the Soil Mechanics and Foundations Division,Proceedings of American Society of Civil Engineering,94(Supplement1):73-91.
Xu S,Wõrman A,Dverstorp B.2001.Heterogeneous matrix diffusion in crystalline rock-implication for geosphere retardation of migrating radionuclides[J].Journal of Contaminant Hydrology,(47):365-378.

