序半群的(∈，∈∨q)-模糊理想刻画

袁凤连， 殷允强

(1.南昌工学院 民族教育一分院，江西 南昌 330108;2.东华理工大学 理学院，江西 南昌 330013)

模糊代数结构的研究起源于Rosenfeld(1971)提出的模糊子群概念。此后各种关于模糊代数的研究呈现出迅速发展的态势，例如，Kuroki(1981)提出并研究了半群中模糊理想的概念。许多作者对半环和序半群的模糊特征进行研究，取得一些成果(Kehayopulu et al.，2006;Zhan et al.，2007;Huang et al.，2007)。近年 来，Kehayopulu 等(2009a，2009b，2008，2006a，2006b，2005)将模糊集、模糊理想、模糊双理想、模糊拟理想以及模糊内禀理想等概念引入到序半群中，促进了序半群在模糊代数学理论的发展。但是，Kehayopulu 提出的模糊理想和模糊双理想的定义大都是借助一种∧和∨运算给出的，而∧和∨两种运算有很大的局限性，在处理实际问题时必然受到限制。最近Yin 等(2010)用“包含，属于”的思想对(∈，∈∨q)-半环上的模糊理想有比较全面系统的研究，得到了一系列比较好的结果，极大的扩充了代数的理论体系。

在此基础上，本论文利用“属于，包含”的思想定义了序半群上的一种模糊子系统，进而研究了序半群上的(∈，∈∨q)-模糊左理想、(∈，∈∨q)-模糊右理想和(∈，∈∨q)-模糊双理想，并利用这些理想给出了正则序半群的若干刻画定理，得到了较好的结果，丰富了序半群的理论体系。

1 预备知识

序半群是一个由非空集合S，一个元运算(·)和一个序关系(≤)构成的代数系统(S，·，≤)，其中(S，·)是一个半群，且满足∀x，y，a，b ∈S，若x≤y，则ax ≤ay，xb ≤yb。

定义2.1 序半群S 的一个子集E 称为S 的左理想，如果满足条件:(1)SE ⊆E;(2)∀x ∈S，若存在y ∈E 满足x ≤y，则x ∈E(Kehayopulu et al.，2006a，2006b)。

定义2.2 序半群S 的一个子集E 称为S 的双理想，如果满足条件:(1)ESE ⊆E;(2)∀x ∈S ，若存在y ∈E 满足x ≤y，则x ∈E(Kehayopulu et al.，2006a，2006b)。

序半群S 上的任意一子集E，记:(E］ ={x ∈S| 存在y ∈E，x ≤y}。

定义2.3 设X 是非空集合，任意一个从X 到区间［0，1］的映射μ 称为X 的模糊子集(Yin et al.，2010)。

设X 是非空集合，设A 是X 的一个子集，χA称为A 的特征函数。

设μ 称为X 的模糊子集，对x ∈X，μ(x)称为μ上的隶属度，X 的所有模糊集记为IF(x)。

定义2.4 设x ∈X，r ∈［0，1］定义X 的模糊子集如下(Yin et al.，2010):

称如上定义的模糊子集μ 为模糊点并记为xr。对于X 上的一个模糊子集μ 和它的模糊点xr有如下关系:

(1)若μ(x)≥r，则xr∈μ;

(2)若μ(x)+ r ≥1，则xrqμ;

(3)若xr∈μ 或xr∈g，则xr∈∨qμ;

(4)若xr∈μ 且xr∈g，则xr∈∧qμ。

定义2.5 μ，v 都是X 上的模糊集，定义μc，μ∩v，μ ∪v 如下(Yin et al.，2010):

μc= 1 - μ(x)，(μ ∩v)(x)= min{μ(x)，v(x)}，(μ ∪v)(x)= max{μ(x)，v(x)}

对任意的x ∈X，μc称为μ 的补集，μ ∩v 称为μ与v 的交集，μ ∪v 称为μ 与v 的并集，μ ⊆v 即为任意的x ∈X 都有μ(x)≤v(x)。

定义2.6 设(S，·，≤)是一个序半群，μ，v ∈IF(S)，定义μ 和v 之间的乘法:

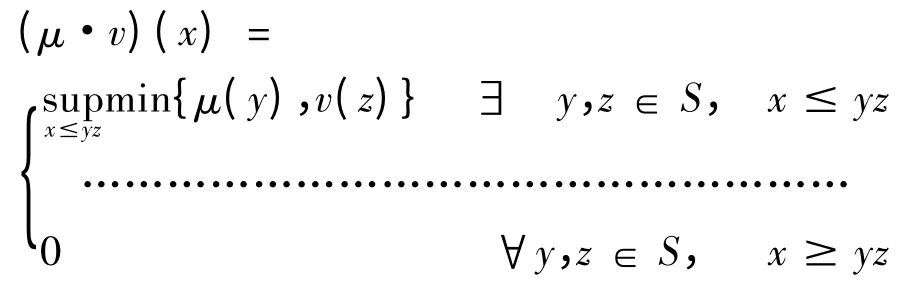
引理2.1 设S(，·，≤)是一个序半群，则A，B ⊆S，则有

(1)当A ⊆B 且仅当χA⊆∨qχB;

(2)χA∩χB= χA∩B;

(3)χA·χB= χ(AB］。

2 主要结果

设(S，·，≤)是一个序半群，以下定义一种IF(S)上的“⊆∨q”一种序半群上“属于或重于”的关系。

注:(1)∀μ，v ∈IF(S)，μ ⊆∨qv 即为∀x ∈S，r ∈(0，1］有xr∈μ 则xr∈∨qμ。

(2)∀μ，v ∈IF(S)，μ ≈v 当且仅当μ ⊆∨qv且v ⊆∨qμ。

定义3.1 设(S，·，≤)是一个序半群，则S的一个子集μ 称为S 的一个(∈，∈∨q)-模糊左(右)理想，如果满足条件:

(F1a)μ·S ⊆∨qμ(S·μ ⊆qμ);

(F2a)∀x，y ∈S，r ∈(0，1］若xr∈μ 群x ≤y，则yr∈qμ。

序半群S 的一个子集μ 称为S 的一个(∈，∈∨q)-模糊理想，当且仅当它既是S 的一个(∈，∈∨q)-模糊左理想，又是S 的一个(∈，∈∨q)-模糊右理想。

定义3.2 设(S，·，≤)是一个序半群，则s 的一个模糊子集μ 称为S 的一个(∈，∈∨q)-模糊双理想，如果满足条件(F2a)及以下条件:

(F3a)μ·μ ⊆∨qμ;(F4a)μ·S·μ ⊆∨qμ。

引理3.1 设(S，·，≤)是一个序半群，∀μ，v∈F(x)，则μ ⊆∨q 当且仅当∀x ∈S 有v(x)≥min{μ(x)，0.5}。

证明:由μ ⊆∨q，∀x ∈S，假设V(x) ＜min{μ(x)，0.5}，则存在r ∈(0，1］使得v(x)＜r＜min{μ(x)，0.5}，也就是xr∈μ 且与已知条件μ ⊆∨q 矛盾，所以v(x)≥min{μ(x)，0.5}。

反之，设对∀x ∈S 有v(x)≥min{μ(x)，0.5}。假设则存在xr∈μ 且由此可得μ(x)≥r，v(x)＜r 及v(x)＜0.5，但是与已知条件v(x)≥min{μ(x)，0.5}矛盾，所以μ ⊆∨qv 成立。

定理3.1 设(S，·，≤)是一个序半群，则S 的一个模糊子集μ 称为S 的一个(∈，∈∨q)-糊双理想当且仅当满足:

(F1b)∀x，y ∈S，μ(xy)≥min{μ(x)，μ(y)，0.5};

(F2b)∀x，y ∈S，y ≤x⇒μ(y)≥min{μ(x)，μ(y)，0.5};

(F3b)∀x，y，z ∈ S，μ(xyz) ≥ min{μ(x)，μ(z)，0.5}。

证明:(F1a)⇒(F1b)(S，·，≤)是一个序半群，μ 是S 的一个模糊子集，设μ 是S 的一个(∈，∈∨q)-糊双理想，则存在x，y ∈S，r ∈(0，1］，使得μ(xy)＜r ＜min{μ(x)，μ(y)，0.5}，即μ(x)＞r 及μ(xy)＜ r ＜0.5，也即是(xy)r与(F3a)μ·μ ⊆∨qμ 矛盾，故(F1b)成立;(F3b)可类似证到。

(F2a)⇒(F2b)另一方面，设(F2a)成立，所以有即得xr∈μ 也就是μ·S ⊆μ，假设，存在x，y ∈S 且y ≤x，t ∈(0，1］使得μ(y)＜t ＜min{μ(x)，0.5}，则μ(y)＜t ＜0.5 及μ(x)＞t，也即是且yt∈μ与(F2a)的条件矛盾，假设不成立，故(F2b)成立。

(F1b)⇒(F1a)反之，若(F1b)成立，假设xr∈μ·S 且则由可得μ(x)＜r 及μ(x)＜0.5，因为对于∀a，b，x ∈S 有x ≤ab 即0.5＞μ(x)≥min{μ(ab)，0.5}≥min{μ(a)，0.5}由此可得μ(x)≥μ(a)及＜μ(x)与(F1b)(F2b)所得的矛盾，故(F1a)成立，类似可证得(F3a)。

(F2b)⇒(F2a)假设存在x，y ∈S 且y ≤x，r ∈(0，1］有xt∈μ 且由此可得μ(x)≥t，μ(y)＜t 及μ(y)+t ＜1，也即是μ(y)＜0.5，因此μ(y)＜min{μ(x)，0.5}与已知条件矛盾，故(F2a)成立。

定理3.2 设(S，·，≤)是一个序半群，则S的一个模糊子集μ 称为S 的一个(∈，∈∨q)-糊双理想当且仅当满足(F2a)和以下:

(F1c)(∀x，y ∈S)(s，t ∈(0，1］)(xt∈μ，ys∈μ⇒(xy)min{t，s}∈∨qμ);

(F2c)(∀x，y，z ∈S)(s，t ∈(0，1］)(xt∈μ，ys∈μ⇒(xyz)min{t，s}∈∨qμ)。

证明:类似于定理3.1 的证明。

结论1 设(S，·，≤)是一个序半群，且A ⊆S，则A 是S 的一个左(右)理想当且仅当χA是S 的一个(∈，∈∨q)-模糊左(右)理想。

证明，很容易直接得到。

结论2 设(S，·，≤)是一个序半群，且A ⊆S，则A 是S 的一个双理想当且仅当χA是S 的一个(∈，∈∨q)-模糊双理想。

证明，很容易直接得到。

设(S，·，≤)是一个序半群，则S 的任意一个模糊子集μ，r ∈(0，1］记＜μ ＞r= {x ∈X| xrqμ}，［μ］r= {x ∈X| xr∈∨qμ}，下面的一个定理描述了S 的(∈，∈∨q)-模糊左(右、双)理想与经典左(右、双)理想之间的关系。

定理3.3 设(S，·，≤)是一个序半群，则S的一个模糊子集μ，则有

(1)μ 是S 的一个(∈，∈∨q)-模糊左(右、双)理想，当且仅当非空子集μr是S 的一个左(右、双)理想对所有的r ∈(0，0.5］;

(2)μ 是S 的一个(∈，∈∨q)-模糊左(右、双)理想，当且仅当非空子集 ＜μ ＞r是S 的一个左(右、双)理想对所有的r ∈(0.5，1］;

(3)μ 是S 的一个(∈，∈∨q)-模糊左(右、双)理想，当且仅当非空子集［μ］r是S 的一个左(右、双)理想对所有的r ∈(0，1］。

证明:只证明(3)，(1)、(2)可类似证明。设μ是S 的一个(∈，∈∨q)-模糊左理想，假设［μ］r≠Ø 对一些r ∈(0，1］。设x，y ∈［μ］r，则可得xr∈∨qμ，yr∈∨qμ.也即是μ(x)≥r 或μ(x)+ r ＞1 且μ(y)≥r 或μ(y)+ r ＞1。又由μ 是S 的一个(∈，∈∨q)-模糊左理想，可得μ(xy)≥min{μ(x)，0.5}及μ(xy)≥min{μ(y)，0.5}，考虑以下两种情况:

第一种情形:若r ∈(0，0.5］则1 - r ≥0.5 ≥r。

①假设μ(x)≥r 或μ(y)≥r，则μ(xy)≥min{μ(x)，μ(y)，0.5}≥r.所以(xy)r∈μ。

②假设μ(x)+r ＞1 且μ(y)+r ＞1，则μ(xy)≥min{μ(x)，μ(y)，0.5}= 0.5 ≥r，所以(xy)r∈μ。

第二种情形:若r ∈(0.5，1］，则r ＞0.5 ＞1 -r。

①假设μ(x)≥r 且μ(y)≥r，则μ(xy)≥min{μ(x)，μ(y)，0.5}≥1 - r，所以(xy)rqμ。

②假设μ(x)+ r ＞1 或μ(y)+ r ＞1，μ(xy)≥min{μ(x)，μ(y)，0.5}≥1 - r，所以(xy)rqμ。

因此无论上面哪种情形都有(xy)r∈∨qμ，都有xy ∈［μ］r，故［μ］r是S 的一个左理想。

相反地，(用反证法)由上面给定的条件成立，假设存在x，y ∈S 使得μ(xy)＜r = min{μ(x)，μ(y)，0.5}，则有xr∈μ 且也即可得x，y ∈［μ］r且(xy)∉［μ］r矛盾，所以对所有的x，y ∈S 有μ(xy)≥min{μ(x)，0.5}因此，μ 是S 的一个(∈，∈∨q)-模糊左理想。

结论3 设(S，·，≤)是一个序半群，且A ⊆S，则A 是S 的一个左(右)理想当且仅当对于所有的x ∈A 使得μ(x)≥0.5 且μ(x)= 0 除外，有S 的模糊子集μ 都是S 的一个(∈，∈∨q)-模糊左(右、双)理想。

证明，直接由定理3.2 可得。

定义3.4 序半群S 称为正则的，如果对∀x∈S，存在y ∈S，使得x ≤xyx。其等价定义为:(1)∀x ∈S ，x ∈(xSx］;(2)∀E ⊆S，E ⊆(ESE］。

引理3.1 序半群S 是正则的当且仅当对S 的每一个右理想R 和对S 的每一个左理想L，均有(RL］= R ∩L(Yin et al.，2008)。

定理3.3 设S 是正则序半群，则下面的两个条件等价:

(1)S 的每一个双理想都是S 的左(右)理想;

(2)S 的每一个(∈，∈∨q)-模糊双理想都是S 的(∈，∈∨q)-模糊左(右)理想。

证明:假设(1)成立，设μ 是S 的一个(∈，∈∨q)-模糊双理想，则对∀x ∈S，子集(xSx］也是S 的双理想，由(1)可知(xSx］也是S 的左理想。又因为S 是正则的，所以∀x，y ∈S，有xy ∈S(ySy］ =(S］(ySY］⊆(ySy］，由μ 是S 的一个(∈，∈∨q)-模糊双理想，所以μ(xy)≥min{μ(yxy)，0.5}≥min{μ(u)}0.5}因此，μ 是S 的一个(∈，∈∨q)-模糊右理想，同样可得μ 是S 的一个(∈，∈∨q)-模糊左理想，μ 是S 的一个(∈，∈∨q)-模糊理想即(2)成立。

反之，假设(2)成立，设B 是S 的任意一个双理想，由结论2 可得特征值χB是B 的一个模糊(∈，∈∨q)-双理想，由条件(2)知特征值χB也是S 的一个模糊(∈，∈∨q)-左(右)理想，由结论1 得B是S 的一个左(右)理想。

定理3.4 设(S，·，≤)是一个序半群，则下列的条件是等价的:

(1)S 是正则序半群;

(2)则对S 的任意一个(∈，∈∨q)-模糊右理想μ 和S 的任意一个(∈，∈∨q)-模糊双理想v 有μ ∩v ⊆∨qμ·v;

(3)则对S 的任意一个(∈，∈∨q)-模糊双理想μ 和S 的任意一个(∈，∈∨q)-模糊左理想v 有有μ ∩v ⊆∨qμ·v;

(4)则对S 的任意一个(∈，∈∨q)-模糊右理想μ 和S 的任意一个(∈，∈∨q)-模糊左理想v 有μ ∩v ≈∨qμ·v。

证明:假设(1)成立，设S 是正则序半群，S 的任意一个(∈，∈∨q)-模糊右理想μ 和S 的任意一个(∈，∈∨q)-模糊双理想v。对∀x ∈S，由S 是正则的，则存在y ∈S，使得x ≤xyx，即有

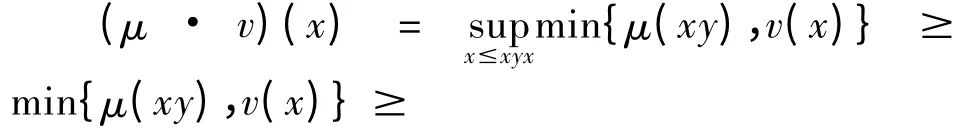
min{min{μ(x)，0.5}，v(x)} = min{μ ∩v(x)，0.5}

由此可得μ ∩v ⊆∨qμ·v，所以(2)成立。(3)可类似证明。

(3)⇒(4)可有定理2.2 直接证得。下证(4)⇒(1)，设R 和L 分别是S 的一个右理想和左理想。由结论1，知χR和χL分别是S 的一个(∈，∈∨q)-模糊右理想和一个(∈，∈∨q)-模糊左理想，又因为χ(RL］= χR·χL≈XR∩XL= χR∩L由引理2.1 直接可得(RL］= R ∩L，再由引理3.1 知S 是正则的。

Huang X K，Li H J，Yin Y Q. 2007. The h-hemiregular fuzzy duo hemirings［J］. International Journal of Fuzzy Systems，9(2):105-109.

Kehayopulu N，Tsingelis M. 2005. Fuzzy bi-ideals in orderd semigroups［J］. Inform. Sci.，171:13-28.

Kehayopulu N，Tsingelis M. 2006. regular ordered semigroups in terms of fuzzy subsets［J］. Inform. Sci.，176:3675-3693.

Kehayopulu N，Tsingelis M. 2006a. Fuzzy interior ideals in ordered semigroups［J］. LobachevskiiJ. Math.，21:65-71.

Kehayopulu N，Tsingelis M. 2006b. Regular ordered semigroups in terms of fuzzy subset［J］. Inform.Sci.，176:3675-3693.

Kehayopulu N，Tsingelis M. 2008.Characterization of some types of ordered semigroups in terms of fuzzy sets［J］. Lobachevskii J. Math.，29 :14-20.

Kehayopulu N，Tsingelis M. 2009a. Fuzzy right，left，quasi-ideals，biideals in ordered semigroups［J］. Lobachevskii Journal of Mathematics Volume 30(1):17-22.

Kehayopulu N，Tsingelis M. 2009b. Intra-regular ordered semigroups in terms of fuzzy sets［J］. Lobachevskii Journal of Mathematics Volume 30(1):23-29.

Kuroki N. 1981. On fuzzy ideals and fuzzy bi-ideals in semigroups［J］.Fuzzy sets Syst.，52:03-205.

Rosenfeld A. 1971. Fuzzy groups［J］. Math. Anal. Appl.，35 :512-517.

Yin Y Q，Li H X. 2008. The characterized by their intuitionistic fuzzy bi-ideals Ital［J］. Pure Appl.Math.，24:169-178.

Yin Y Q，Wang J M. 2010. Fuzzy Hemirings［M］. Scinence press USA Inc:10-27.

Zhan J，Dudek. 2007. W A. Fuzzy h-ideal of hemir-ings［J］. Inform.Sci.，177(3):876-886.