基于最小支持的2.5维直流电阻率正则化反演研究
李 曼, 林文东,2
(1.东华理工大学核工程与地球物理学院,江西 南昌330013;2.辽宁省有色地质局103 队,辽宁 丹东118008)
地球物理解释工作的目的是使解释结果逼近真实地质模型,正则化是得到稳定解的重要手段。正则化方法中稳定因子的设计与正则化因子的选择是两项重要研究内容。
Tikhonov 等(1977)提出了正则化方法

式中,P(α,m)是总的目标函数,α 是正则化因子,φd(m)是数据目标函数,φm(m)是模型约束目标函数,也称稳定因子。
稳定因子的主要功能是对模型解的空间进行限制,以减少多解性,求得稳定解(Zhdanov,2002),稳定因子的设计是正则化方法中的重要研究内容。在地球物理学中,可以使用的稳定因子有很多,根据实际问题的不同,可以选择的稳定因子也有不同。本文为实现陡变边界反演,研究了最小支持稳定因子。
最小支持稳定因子最先是由Last 等(1983)提出并运用于重力数据的反演解释;Mehanee 等(2002)在进行了最小支持稳定因子提高块状结构分辨率的研究;Candansyar(2002)在其二维大地电磁的反演的文章中进行了不同稳定因子的比较;在一篇关于地震应用的文献中,Portniaguine 等(2004)对聚焦参数的取值进行了分析,提出了聚焦参数依据计算机字长的选择方法;Zhdanov 等(2004)在3D 重力张量的正则化反演中使用了该稳定因子,使反演结果更加接近真实值;刘小军等(2007)在二维大地电磁数据的聚焦反演算法中运用了类似的正则化技术,取得了较好的反演效果;Vignoli 等(2012)在一维条件下对最小支持稳定因子中的聚焦参数的选择取进行了讨论。
要想得到稳定解,就需要使得方程的右边两项达到较好的平衡,因此选择恰当的正则化因子同样是十分必要的。早期地球物理学学者采用一些经验算法确定,随着越来越多的学者对这一方面关注,提出大量的正则化因子选取方法。其中,以Hansen 所提出的L 曲线法最为著名。该方法是基于数据误差水平未知的启发式后验选取方法,在双对数坐标下形成单调递减的曲线,类似于字母“L”,故称为L 曲线法。Hansen(1992)首次提出L 曲线准则方法;此后几年,Hansen 等(1993)对该法进行了系统的研究,完善了L 曲线法的理论;Hansen 等(1999)给出了较实用的L 曲线法计算技术。
在地球物理方面,Li 等(1999)首次在他的文章中将“L 曲线法”引入地球物理反演中;Farquharson 等(2000)在他们的文章中对广义交叉原理(GCV)和“L 曲线法”在非线性反演问题中选择正则化因子的对比进行了论述;近年来,该方法得到广泛关注,王振杰等(2004,2005)研究了用L 曲线法确定半参数模型中的平滑因子和一种解算病态问题的两步解法;赵烈加等(2007)研究了基于L 曲线准则的谱反演算法;姜祝辉等(2011)在合成孔径雷达资料反演海面风场中也使用了正则化方法;于胜杰等(2012)研究了选权拟合法进行GPS 水汽层析解算;陶肖静等(2012)研究了半参数模型中影响正则化因子的因数;李伦等(2013)研究了基于正则化方法的高频地波雷达海浪方向谱反演,这些研究中均使用了L 曲线准则确定正则化因子。
本文通过简单的点与直线关系对“L 曲线法”进行了改进;该方法不需要Hansen 经典算法计算曲线曲率,计算简间、高效,同时可以有效的去除“假”正则化因子,在求解实际地球物理问题中应用效果显著。文章使用修正的L 曲线法自动选取正则化参数,采用最小支持稳定因子作为模型约束目标函数,同时给出了形式上的模型参数表示方法,采用正则化的共轭梯度法对目标函数极小化。将最小支持稳定因子应用到算例分析中,对理论模型进行试算,同时对聚焦参数的取值进行了讨论,对比分析后,证明了本文所采用的最小支持稳定因子表示方法及参数选择算法的正确高效,最小支持稳定因子具有更好的聚焦能力、有利于实现陡变边界反演。
1 最小支持稳定因子及聚焦参数的选取
稳定因子的主要功能是对模型解的空间进行限制,以减少多解性,求得稳定解。地球物理学中常用的稳定因子主要有最小范数稳定因子、最大平滑稳定因子等,但这两者都是基于模型光滑,当模型出现突变时,这两种稳定因子计算结果仍是渐变的,不利于地质资料解释。最小支持稳定因子:
式中,β 为聚焦参数。
Zhdanov(2002)给出了稳定因子的伪二次统一表示:

其中函数we是关于m 的一个非线性函数,在这种情况下,由式(3)所确定的函数s(m)不是二次的,这就是称其为“伪二次”函数的原因。
用稳定因子的“伪二次”式(3),可以把对应的Tiknonov 正则化方程(1)变为:
最小支持稳定因子在正则化问题中的一个简化的“假的二次”形式,可以使用如下表示方法以达到在地球物理问题中得到近似正则化解的目的。
对于最小支持稳定因子SMS(m)来说,假定若mapr= 0,则
根据最小支持稳定因子的性质,在反演中模型会尽可能的集中,从而可以区分物性差异较大的界面。对于最小支持稳定因子来说,聚焦参数β 的取值也对反演结果具有很大的影响。Portniaguine 等(2004),Vignoli 等(2012)的研究表明聚焦参数的取值与计算机的精度有关,下面介绍Vignoli 的选择方法。当m = mapr时,为避免奇点β 的取值要满足如下:

其中eps 是计算机浮点相对精度,在其文章中,β 按如下公式取值:
其中max(m - mapr)是m - mapr向量中的最大元素。
2 L 曲线法则及修正
2.1 Hansen 的L 曲线法
正则化因子作为数据目标函数和模型约束目标函数的权重系数,若正则化因子过大则产生的结果主要拟合先验模型,若正则化因子过小则产生的结果主要拟合观测数据。若在这两种情况之间取值,就可以得到折中解,该解在某种程度上不仅可以满足精度要求,也可以保证解的稳定性。
由Hansen 等提出的L 曲线技术是一种基于数据误差水平未知的启发式后验选取正则化因子的方法,该方法以log-log 尺度来描述φd(m)与φm(m),其正则化因子α 的取值为双对数曲线上曲率的最大值,一般是其“隅角”所对应的位置,如图1中α0所示位置。
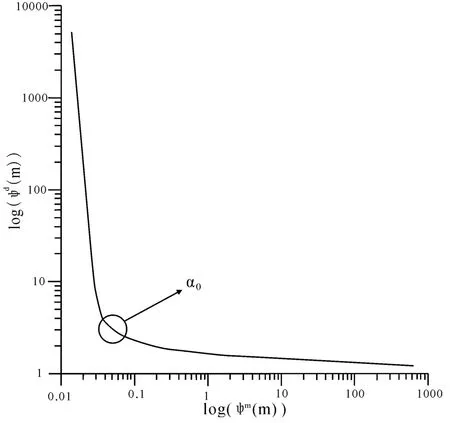
图1 L 曲线Fig.1 L-curve
在Hansen 的经典论文中给出了通过曲线的曲率半径计算“隅角”的方法。地球物理的反演问题是已知观测数据求与其对应模型的过程。设d 为观测数据向量,m 是模型参数向量,A 为把地球物理模型映射到理想数据的函数,正问题可表示为,

式中A 为正演算符,Tikhonov 正则化的基本思想是将解的范数作为先验信息考虑,则问题的求解(假定正问题是线性的)将转化为求解以下问题的最小值:

对于一般的m × n 矩阵A,一定存在正交阵U= (u1,u2,Λ,un)∈Rm×m和V = (v1,v2,…,Vn)∈Rn×n,可以使得
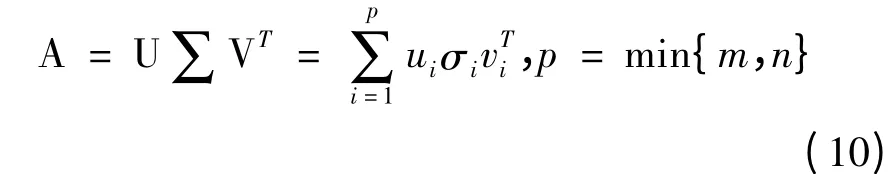
其中σi表示奇异值,且σ1≥σ2≥…≥σp≥0 是递减的顺序排列,∑= diag(σ1,σ2,…,σp)。ui为左奇异向量,相互正交,即有UTU = Im,vi为右奇异向量,相互正交,即有VTV = In。从而可以得出:
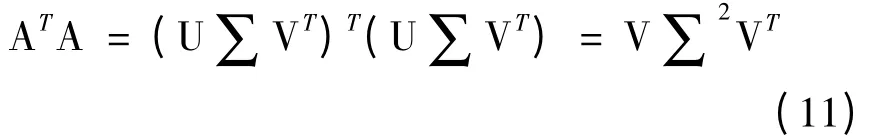
为了运算简便,令正则化参数α = λ2。从而方程组A(m)= d 的Tikhonov 正则化所对应的解可以写为:
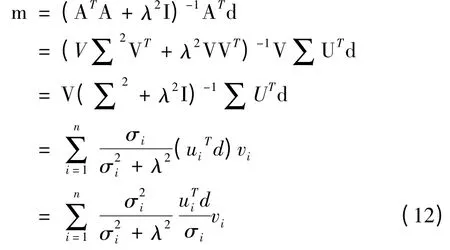
对于Tikhonov 正则化方程组来说,应用奇异值分解可以得到:

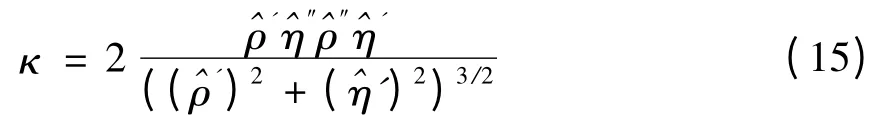
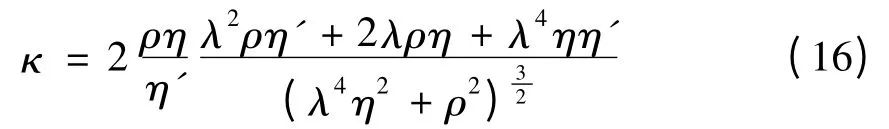
求κ(η)的最大值便可以得到合适的正则化因子。
2.2 修正的L 曲线法
对于Hansen 的L 曲线准则来说,若知道L 曲线的参数表达式,即函数η(α)和ρ(α)的精确表达式,采用曲率公式求曲率的最大值可以得到合适的正则化因子。但在实际应用中,很难得到精确的η(a)和ρ(α)表达式,此时可以采用三次样条插值的方法来近似的确定L 曲线的“隅角”,从而选取适当正则化因子,其主要思想为:将节点个数逐步增加,形成的参数样条可以更好的逼近L 曲线,选取的最优正则化因子为最终样条上曲率最大的点。
曲率公式(15)中含有两个一阶导数和两个二阶导数,实际应用中常常会导致计算结果不稳定,Hansen 对其进行了简化,得到了只含有一个一阶导数的公式,同时可以证明L 曲线是单调递减的曲线,公式在理论上可以很好的确定正则化因子,但在实际应用中,L 曲线可能出现两个“拐点”的情况,如图2 所示。
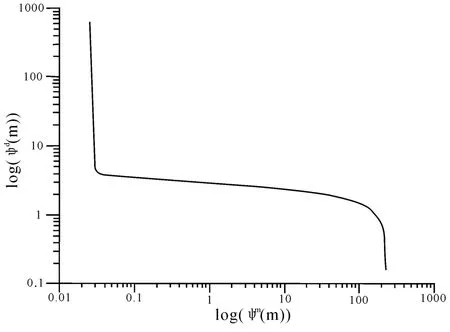
图2 实际应用中可能出现的L 曲线形状Fig.2 The shape of the L curve may occur in practical application
针对这一情况,对L 曲线准则进行了改进,原理基于点与直线的关系以及点到直线的距离,具体算法如下:
(1)给定初始的正则化因子αi(至少四个,水平部分两个,竖直部分两个),及其对应的(pi,qi)
(2)关于βi= logαi对pi和qi分别做三次样条插值,分别将插值函数记为p(β)和q(β);
(3)找到L 曲线即曲线(p(β),q(β))的两个端点,确定一条直线,写出直线表达式Ax + By + C= 0;
(4)在L 曲线上任选一点,(x0,y0),将其带入直线表达式,若Ax0+By0+C <0,则保留,若Ax0+By0+ C ≥0,则舍弃,直到所有L 曲线上的点都选完;
(5)从选取的点中任取一点,(x1,y1),带入点到直线公式计算出每一点到直线的距离,计算距离最大值的点,设其为(p(β0),q(β0)),记α0= 10β0;
(6)求解α0所对应的正则化问题,记正则化解为mα0,由正则化解可以得到新的点对(p0,q0);
(7)将新的点对(p0,q0)和α0加入到步骤(1)的点对和参数中;
(8)将步骤(7)中得到的点对和参数重复步骤(2)到步骤(7)的过程,直至收敛。
相对于一般的L 曲线准则来说,修正算法增加了步骤(3),(4)和(6),去掉了“假的”正则化因子,可以使选择正则化因子更符合实际地球物理问题,为后续的研究工作打下坚实基础。
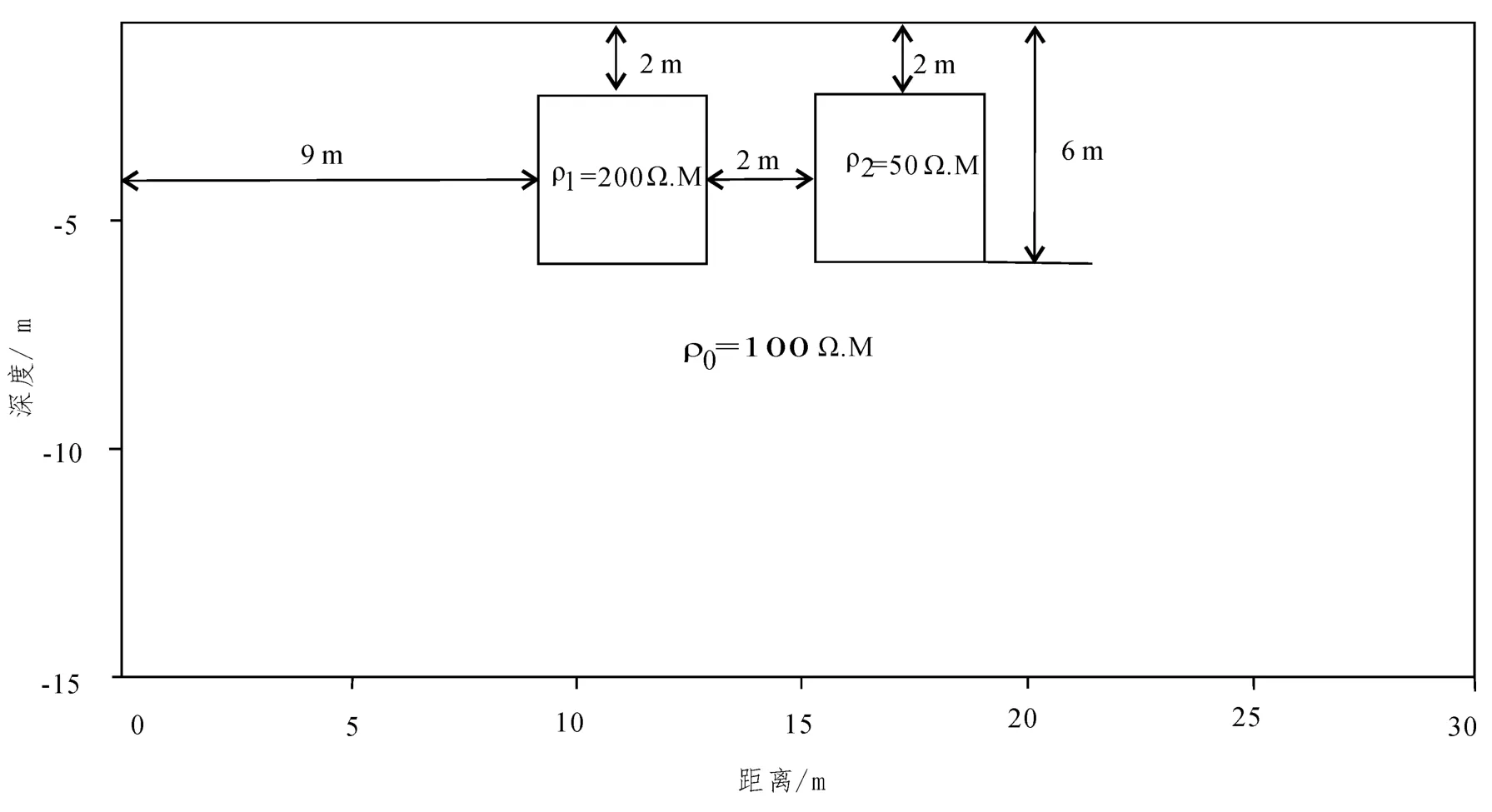
图3 组合模型示意图Fig 3 Diagram of multiple model
3 算例分析
在ρ0=100 Ω·m 背景电阻率条件下,存在两个截面为正方形(边长4 m)的水平棱柱,其中高阻体,低阻体ρ2=50 Ω·m,相距2 m,异常体顶部埋深2 m,如图3 所示。地表采用30个电极,电极距1 m,采用温纳-装置进行高密度电阻率测量。
采用正演计算结果(加入0.5%的白噪声)作为反演数据集,运用共轭梯度法、修正的L 曲线法算法,分别最小范数稳定因子、最大平滑稳定因子及最小支持稳定因子对进行反演试算。反演结果(图4,5,6,7)。
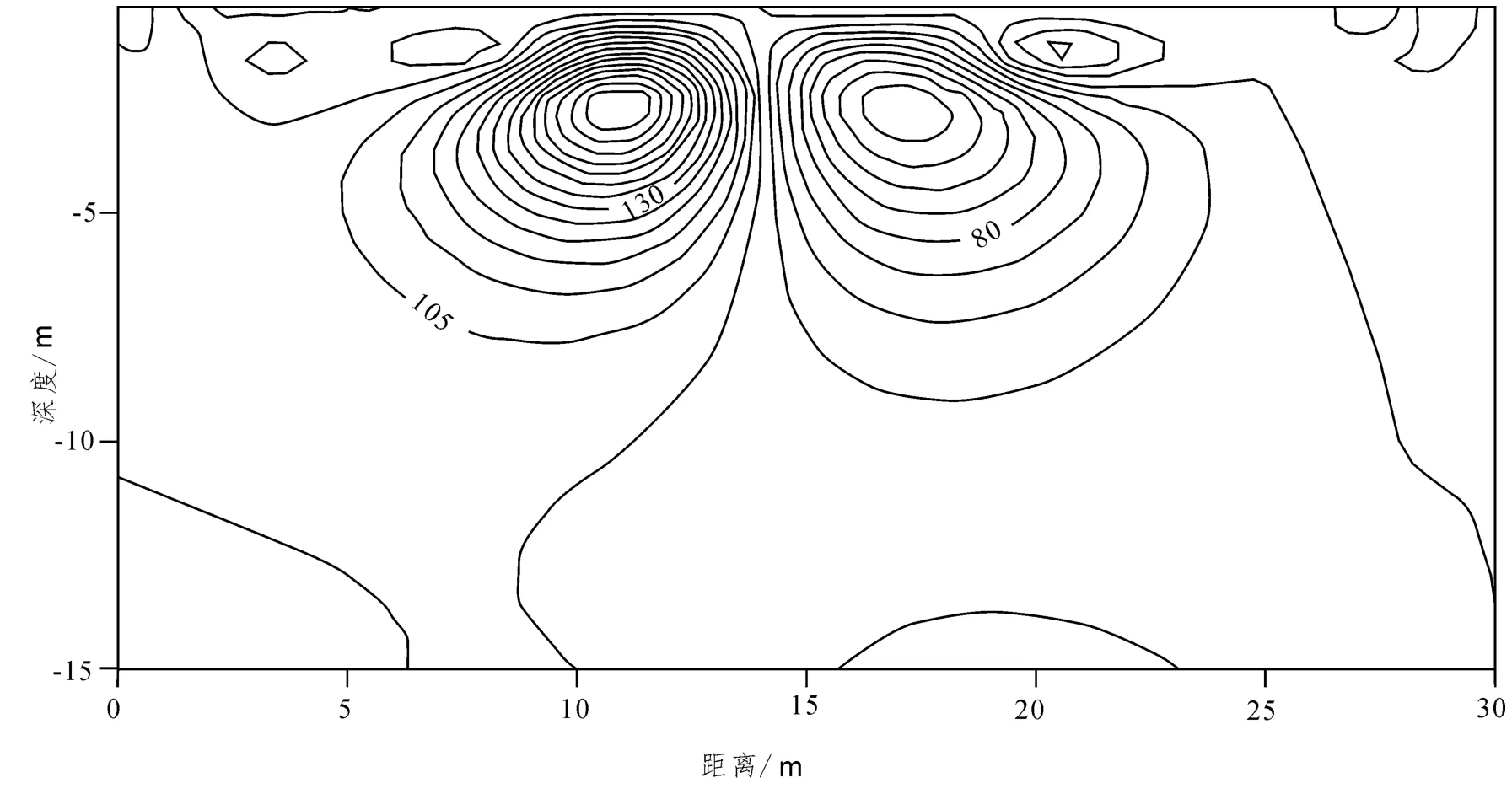
图4 稳定因子为最小范数稳定因子时的反演结果Fig.4 The inversion results of the minimum norm stabilizing factor
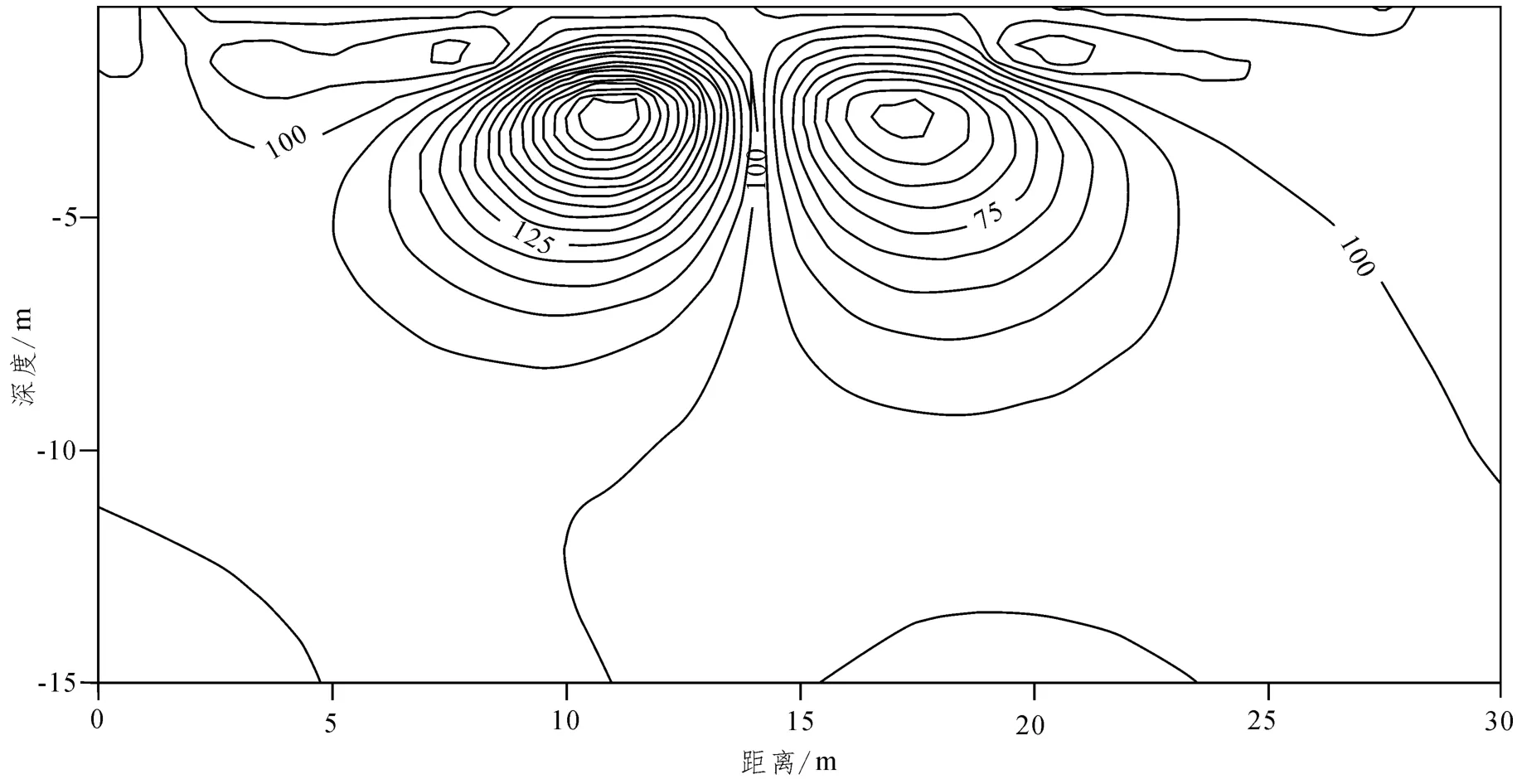
图5 稳定因子为最大平滑稳定因子(一阶)时的反演结果Fig.5 The inversion results of the maximum smoothness stabilizing factor (first-order derivative)
从图4 ~图7 中可以看出,反演结果与实际的地电模型吻合程度很好。从反演断面图可以看出,在使用修正的L 曲线法自动选取正则化因子的情况下,采用不同的稳定因子,得到的反演结果都能够较好的反应真实的地下地质结构。在同样地误差精度和迭代次数情况下,(1)最小范数稳定因子和最大平滑稳定因子(一阶、二阶)的反演断面图得出,反演结果能与异常体吻合,但边界为平滑过度。(2)相比于最小范数稳定因子和最大平滑稳定因子,最小支持稳定因子的反演结果能够更好的反应陡变异常体边界,异常体深度对应优于最小范数与最大平滑稳定因子。
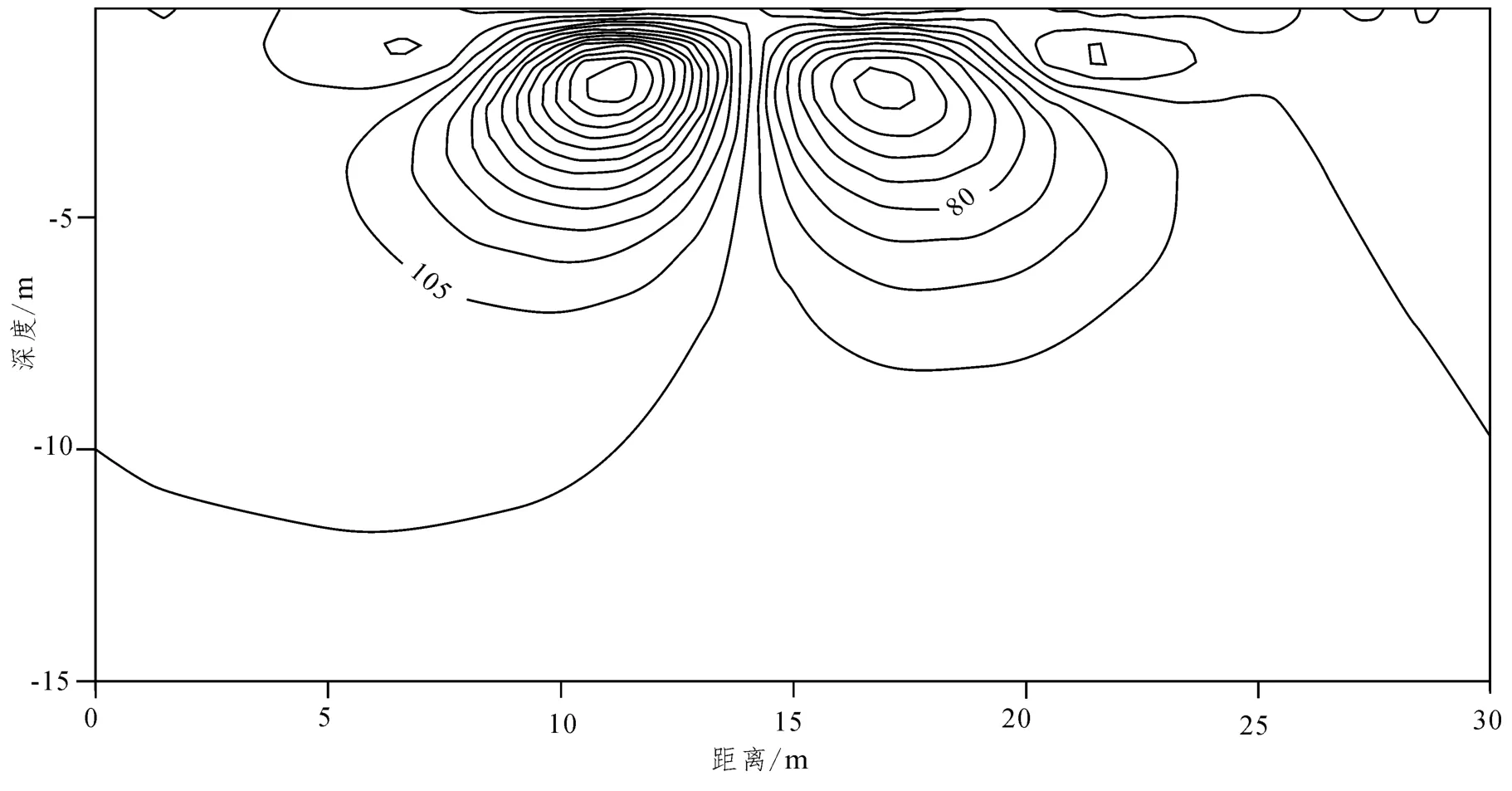
图6 稳定因子为最大平滑稳定因子(二阶)时的反演结果Fig.6 The inversion results of the maximum smoothness stabilizing factor (second-order derivative)

图7 稳定因子为最小支持稳定因子时的反演结果Fig.7 The inversion results of the minimum support stabilizing factor
4 结论
地球物理反问题存在多解性和不稳定性,正则化是得到稳定解的重要手段之一。正则化方法中稳定因子的设计与正则化因子的选择是两项重要研究内容。本文开展了L 曲线法自动选取正则化因子的修正算法及最小支持稳定因子的研究工作,应用非线性共轭梯度法对2.5 维直流电阻率反问题进行了试算,结果表明:
(1)针对实际地球物理问题,运用了点与直线关系和点与直线距离对L 曲线法进行了修改,提出了一种修正的L 曲线法,该方法计算简单、高效,有效了避免选择过程落入“假”正则化因子区间。
(2)最小支持稳定因子相对于最小范数稳定因子和最大平滑稳定因子具有更好的识别陡变异常体边界的能力。
姜祝辉,黄思训,何然,等. 2011. 合成孔径雷达资料反演海面风场的正则化方法研究[J].物理学报,60(6):1-8.
李伦,吴雄斌,龙超,等. 2013. 基于正则化方法的高频地波雷达海浪方向谱反演[J].地球物理学报,56(1):219-229.
刘小军,王家林,陈冰,等.2007.二维大地电磁数据的聚焦反演算法探讨[J].石油地球物理勘探,42(3):338-342.
陶肖静,朱建军,田玉淼. 2012.半参数模型中影响正则化因子的因素分析[J]. 武汉大学学报·信息科学版,37(3):298-301.
王振杰,欧吉坤,曲国庆.2004. 用L 曲线法确定半参数模型中的平滑因子[J]. 武汉大学学报·信息科学版,29(7):651-653.
王振杰,欧吉坤,柳林涛. 2005.一种解算病态问题的方法—两步解法[J].武汉大学学报·信息科学版,30(9):821-824.
于胜杰,柳林涛. 2012. 利用选权拟合法进行GPS 水汽层析解算[J].武汉大学学报·信息科学版,37(2):183-186.
赵烈加,刘卫,陈小华,等. 2007.基于L 曲线准则的T2 谱反演算法研究[J].石油天然气学报,29(6):82-86.
Candansayar M E. 2002. Two-dimensional inversion of magnetotelluric data with CG and SVD:A comparisonal study of different stabilizers[J]. SEG Technical Program Expanded Abstracts,21(1):669-672.
Farquharson C G,Oldenburg D W. 2000. Automatic estimation of the trade-off parameter in nonlinear inverse problems using the GCV and L-curve criteria[J]. SEG Expanded Abstracts,19(1):265-268.
Hansen P C. 1992. Analysis of discrete ill-posed problems by means of the L-curve[J].Siam Review,34(4):561-580.
Hansen P C,O’Leary D P. 1993. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM J. Sci. Comput,14:1487-1503.
Hansen P C. 1998. Rank-Deficient and Discrete Ill-Posed Problems[M]. Philadelphia:SIAM.
Hansen P C. 1999. The L-curve and its use in the numerical treatment of inverse problems[M]. Denmark:Department of Mathematical Modeling.
Last B J,Kubik K. 1983. Compact gravity inversion[J]. Geophysics,48(6):713-721.
Li Y G,Oldenburg D W. 1999. 3-D inversion of DC resistivity data using an L-curve criterion[J].SEG Expanded Abstracts,18(1):1-4.
Mehanee S,Zhdanov M S. 2002. Two-dimensional magnetotelluric inversion of blocky geoelectrical structures[J]. Journal of geophysical research,107(B4):2065.
Portniaguine O,Castagna J P. 2004. Inverse spectral decomposition[J].SEG Expanded Abstracts,23(1):1786-1789.
Tikhonov A N,Arsenin V Y. 1977. Solution of Ill-posed Problems[M].Washing.D.C:V.H.Winston and Sons.
Vignoli G,Deiana R,Cassiani G. 2012. Focused inversion of vertical radar profile (VRP)traveltime data[J]. Geophysics,77(1):9-18.
Zhdanov M S. 2002. Geophysical Inverse Theory and Regularization Problems[M]. Netherlands:Elsevier.
Zhdanov M S,Ellis R,Mukherjee S. 2004. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J].Geophysics,69(4):925-937.

